Python实现BP神经网络详解及代码分享

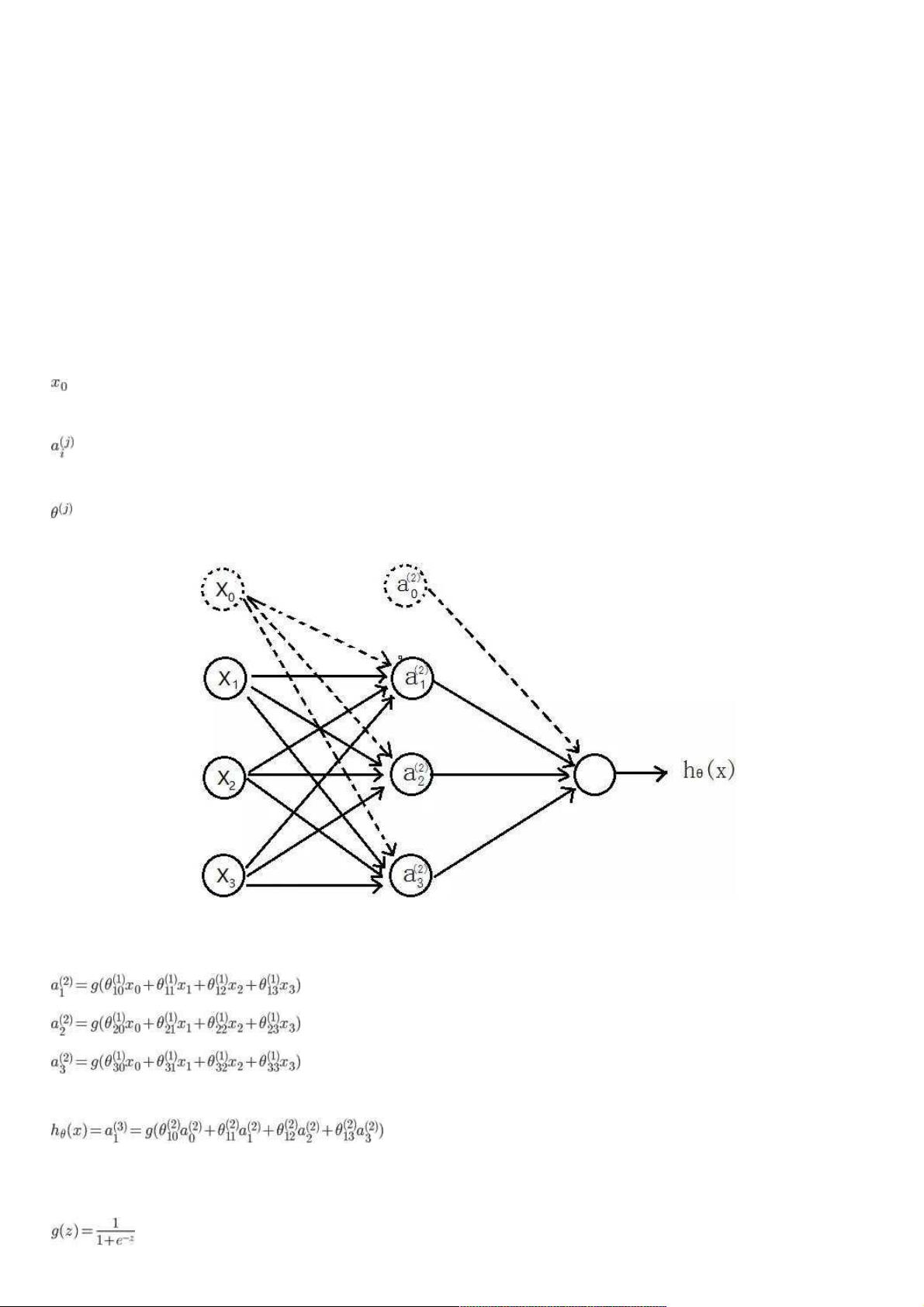
"这篇文章主要介绍了如何使用Python实现BP神经网络，并提供了相关代码示例，旨在帮助读者学习和理解BP神经网络的基本概念、结构以及训练过程。" 在机器学习领域，反向传播（Backpropagation，简称BP）神经网络是一种广泛应用的多层前馈神经网络模型。这种网络通过梯度下降法优化权重参数，以最小化预测输出与实际值之间的误差，从而进行分类或回归任务。Python由于其简洁易读的语法，成为了实现各种算法的首选语言，包括BP神经网络。 首先，BP神经网络的基本结构通常包括输入层、隐藏层和输出层。在给定的例子中，输入层有三个单元，一个用于偏置项，通常设置为1。隐藏层和输出层的单元数量由网络设计决定。权重矩阵`Wij`连接相邻层的节点，表示从第j层到第j+1层的映射关系。神经元的激活函数通常是S型函数（Sigmoid函数），它将节点的加权输入转换为0到1之间的连续值，以模拟生物神经元的非线性响应。 网络的前向传播过程是通过输入层传递数据，经过激活函数处理后进入隐藏层，再由隐藏层传递到输出层。计算过程中，每个神经元的输出取决于其输入和连接权重。 代价函数（Cost Function）用于衡量模型预测的准确度，一般采用交叉熵损失函数（Cross-Entropy Loss）或均方误差（Mean Squared Error）。在这个例子中，如果网络有K个输出单元，代价函数会累加所有输出单元的误差。同时，为了防止过拟合，通常会加入正则化项（Regularization），这里采用L2正则化，它对所有层的权重参数`θ`进行惩罚，但不包括偏置项`θ(0)`。 在Python中，实现代价函数时，首先需要获取所有权重参数`nn_params`的形状，然后根据形状还原各层的权重矩阵`Theta1`和`Theta2`。接着，计算代价函数，包括前向传播计算网络输出以及加入正则化的部分。正则化项的计算是通过累加所有层（不包括输入层）的权重矩阵的平方和，乘以正则化系数`Lambda`。 整个BP神经网络的训练过程包括前向传播计算输出，反向传播计算梯度，然后更新权重。这个过程通常在多个数据样本上迭代，直到达到预设的迭代次数或误差阈值。在Python中，可以使用优化库如scikit-learn或自定义的梯度下降算法实现这一过程。 通过阅读和理解这篇文章，你可以掌握BP神经网络的基本原理，学会如何用Python实现一个简单的神经网络模型，并了解如何应用正则化来改善模型的泛化能力。对于初学者，这是一个很好的起点，可以进一步深入到深度学习和其他更复杂的神经网络结构。