MATLAB在数值分析中的应用：插值与积分

该文档是关于使用MATLAB进行数值分析，包括插值和积分的实践报告。作者是一名计算机科学与技术专业的学生，通过MATLAB软件实现了拉格朗日插值、牛顿插值、埃特金逐次线性插值以及复化梯形公式、复化辛卜生公式和复化柯特斯公式来解决实际问题。 在数值分析中，插值是一种常见的数学方法，用于找到一个多项式函数，使得该函数在给定的一组数据点上精确匹配这些点的值。MATLAB提供了强大的工具来实现这一过程。文档中提到了三种插值方法： 1. **拉格朗日插值法**：通过构造插值基函数来构建插值多项式，每个基函数在除自己对应的数据点外的其他点都为0。MATLAB中可以通过循环和`poly()`函数来实现，`conv()`函数用于计算多项式的乘积。 2. **牛顿插值法**：也称为向前差分或Newton-Cotes公式，基于函数在数据点处的导数信息构建插值多项式。MATLAB编程思路与拉格朗日插值类似，但涉及函数的导数计算。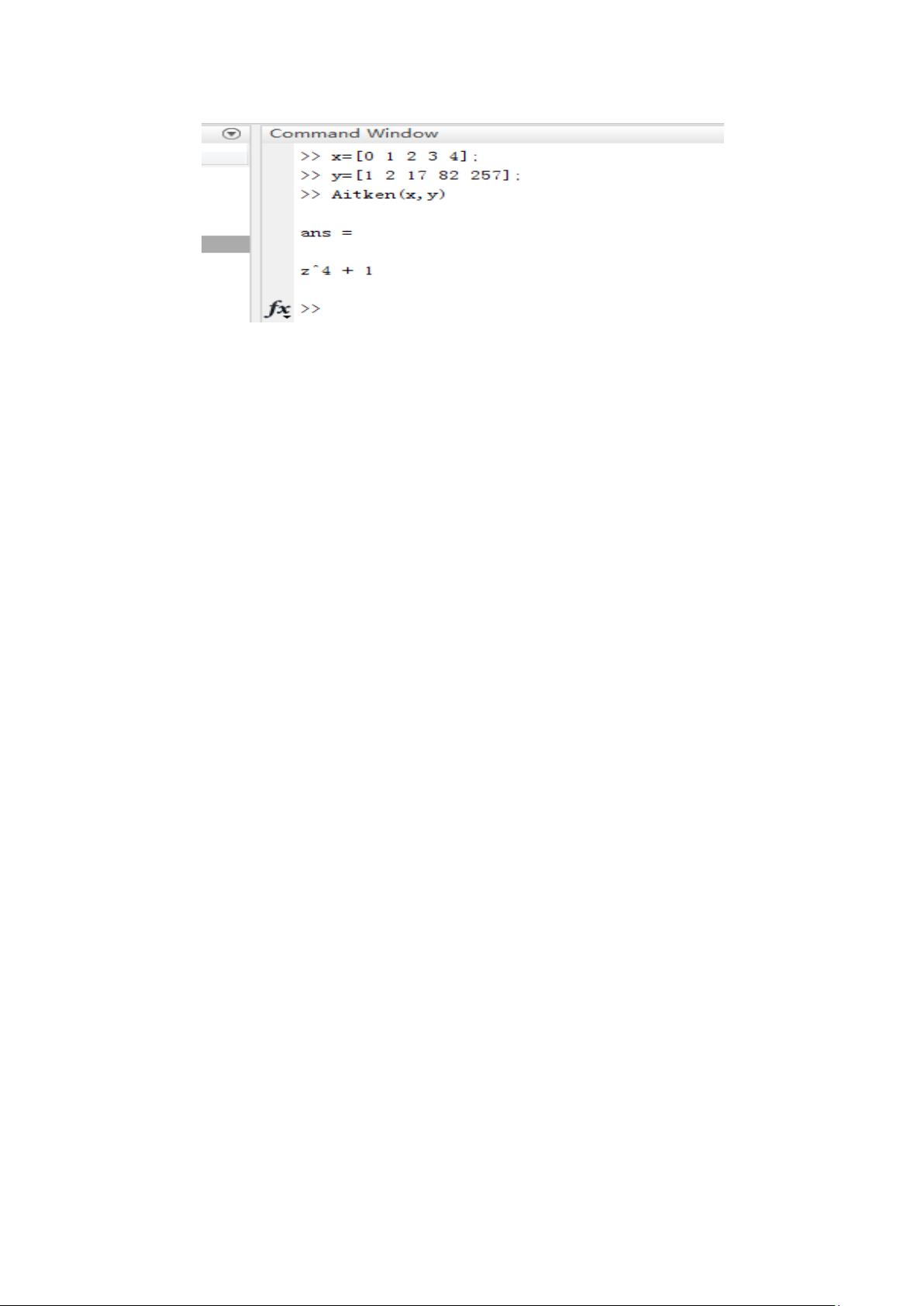 3. **埃特金逐次线性插值法**（Aitken插值）：这是一种减少插值误差的方法，通过递归地去除高次项来提高插值的精度。 在积分方面，数值积分是无法直接解析求解积分时使用的一种策略。文档中提到的三种复化公式： 1. **复化梯形公式**：将积分区间分割成多个小的子区间，然后利用梯形法则近似每个子区间的积分，最后将所有梯形面积相加得到整体的近似值。 2. **复化辛卜生公式**（Simpson's rule）：类似于梯形公式，但每个子区间使用二次多项式近似，对偶数个子区间使用三次样条函数，从而提高精度。 3. **复化柯特斯公式**（Curtiss' rule）：基于更高阶的插值多项式，如四次多项式，提供更高的近似精度。 在MATLAB中，这些问题的解决通常涉及创建函数句柄，定义积分区间，然后调用相应的数值积分函数，如`quad`或`quadl`等。 总结来说，这篇文档详细介绍了如何使用MATLAB实现数值分析中的插值和积分问题，对于学习和理解数值计算方法以及MATLAB编程技巧具有很高的参考价值。通过实际案例和代码演示，可以帮助学生深入理解这些概念并应用于实际问题中。