SPSS线性回归分析步骤与应用

"回归分析是统计学中一种重要的数据分析方法，尤其在SPSS软件中，它可以帮助用户理解两个定距变量之间的因果关系。本资源主要讲述了回归分析的步骤，包括制作散点图、数据预处理、直线回归分析、残差分析和识别强影响点以及多重共线性问题。此外，还详细解释了线性回归的原理、适用条件以及在SPSS中的操作方法。" 回归分析是一种统计方法，用于研究两个或多个变量之间的关系，特别是当一个变量（自变量）可能影响另一个变量（因变量）时。在SPSS中，线性回归是一个常用工具，它基于变量间存在线性关系的假设。线性回归通过建立一个数学模型来描述这种关系，模型通常表示为y = a + bx，其中y是因变量，x是自变量，a是截距，b是回归系数。 回归的步骤如下： 1. **散点图**：首先，通过绘制自变量和因变量的散点图，可以直观地观察两个变量之间是否存在某种趋势或模式。 2. **数据预处理**：检查数据的分布，确保数据满足回归分析的基本假设，例如独立性、正态性和方差齐性。如果数据存在问题，可能需要进行转换或者清洗。 3. **直线回归分析**：使用SPSS的线性回归功能，将自变量全部输入模型，通过最小二乘法来估计回归系数和截距。最小二乘法旨在找到一条直线，使得所有数据点到直线的垂直距离（即残差）之和最小。 4. **残差分析**：分析残差可以帮助我们评估模型的拟合度和假设的合理性。如果残差呈现出特定的模式，可能意味着模型需要改进或数据存在异常。 5. **强影响点诊断**：识别并处理可能严重影响模型结果的异常值，这些点称为强影响点。 6. **多重共线性判断**：当自变量之间高度相关时，可能存在多重共线性问题，这可能会影响系数的稳定性和预测准确性。可以通过相关性矩阵、方差膨胀因子（VIF）等指标来诊断。 线性回归的适用条件包括： - **线性趋势**：自变量和因变量之间的关系应该是线性的。 - **独立性**：因变量的观测值之间是相互独立的。 - **正态性**：自变量的线性组合应服从正态分布。 - **方差齐性**：不同自变量组合下的因变量方差要一致。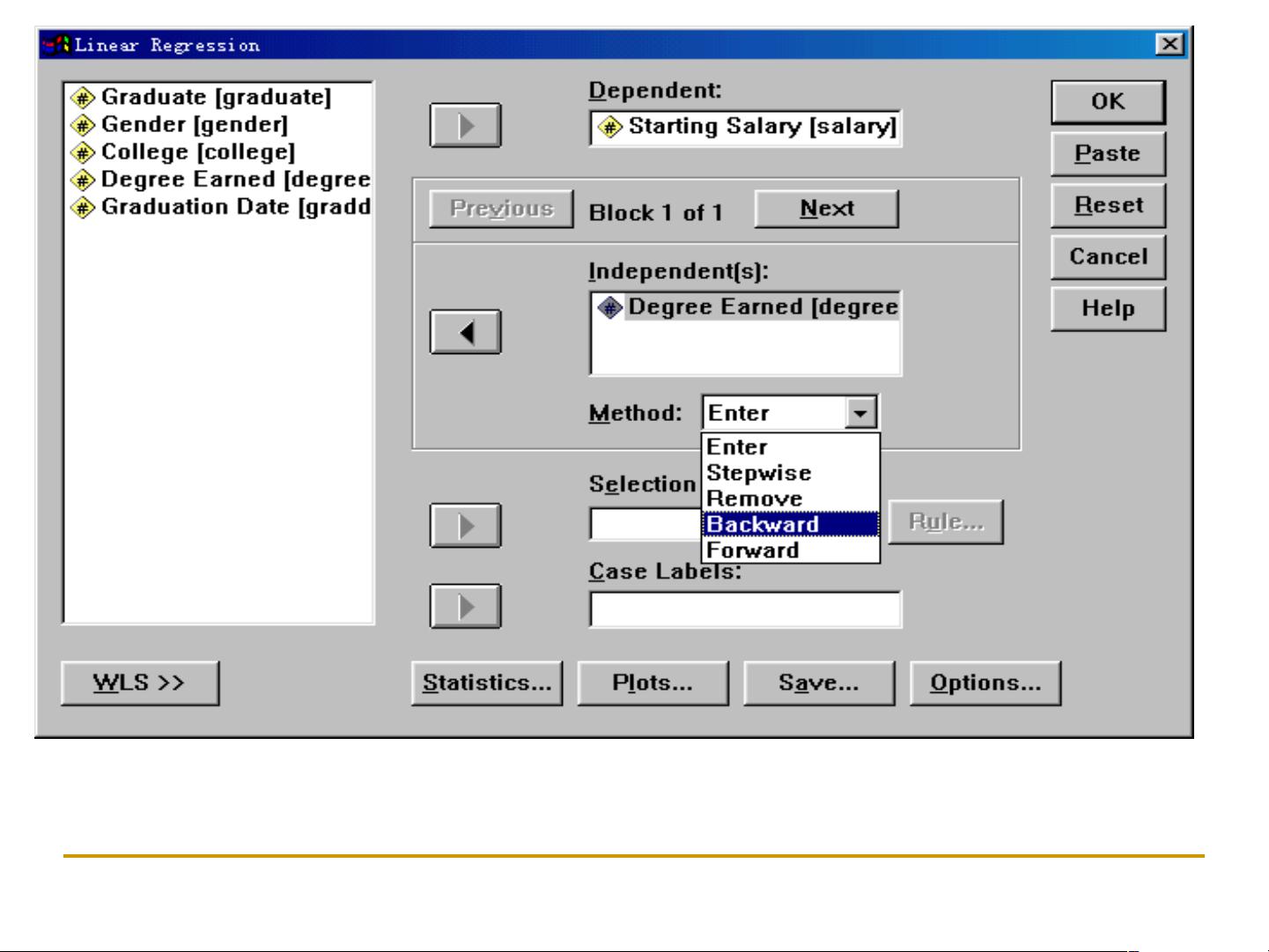 在SPSS中，线性回归可以通过“Enter”或“Stepwise”方法进行。"Enter"方法将所有自变量一次性放入模型，而"Stepwise"方法则根据贡献度逐步选择自变量，可以自动剔除对模型贡献较小的变量。 通过理解和应用这些步骤，我们可以利用SPSS进行有效的线性回归分析，从而更好地理解数据中的关联性，并进行预测。