卷积神经网络（CNN）权值优化与误差反向传播解析

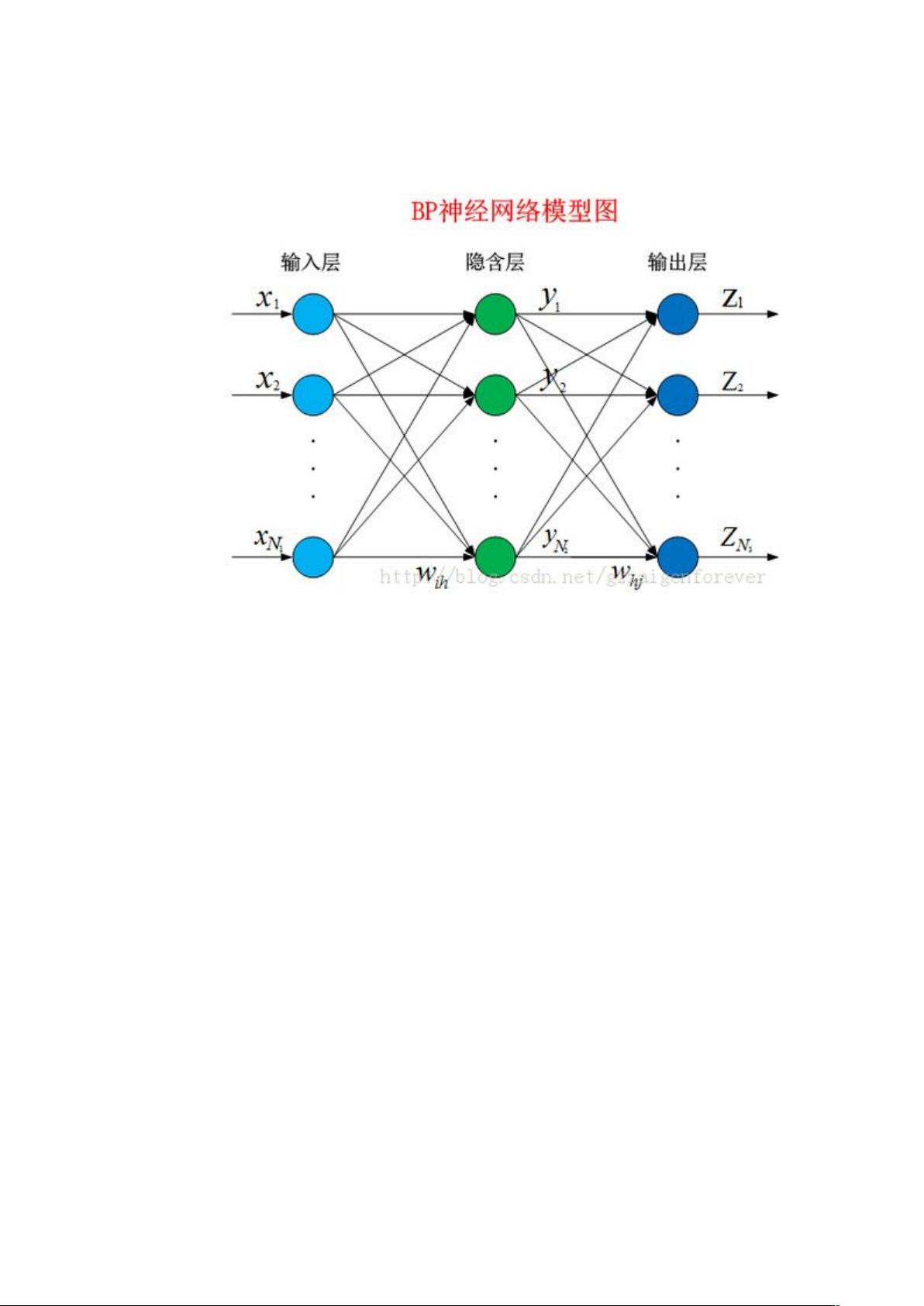
本文主要探讨了卷积神经网络（CNNs）中的权值优化算法，特别是结合反向传播（BP）算法在神经网络中的应用。文章以三层BP网络为例，阐述了网络中各层神经元的输入、输出计算以及学习过程中的误差函数和权重更新规则。同时，还讨论了卷积神经网络的特异性，如卷积层与池化层间的误差敏感值计算，并以实例说明了上采样（unsample）在反向传播过程中的作用。 在BP神经网络中，反向传播算法是通过最小化实际输出与期望输出的误差平方和来调整权重的过程。以三层网络为例，隐藏层第j个神经元的输入由其前一层所有神经元的输出与权重的乘积累加而成，即Netj = ∑(Wji * Xi)。接着，通过激活函数g(netj)计算神经元的输出Oj，通常采用Sigmoid函数g(x) = 1 / (1 + exp(-x))。类似地，输出层的神经元也有类似的计算方式，误差E由所有神经元输出与期望输出的差的平方和构成。权重更新则依赖于误差梯度，通过误差敏感值（δ）和链式法则来实现，即式（1）、式（2）和式（3）所示，此处“◦”表示逐元素乘法。 卷积神经网络（CNNs）的结构和连接方式比BP网络复杂，其权值优化涉及到更特殊的计算方法。在输出层，由于通常与前一层全连接，其误差敏感值的计算与BP网络相同。然而，当卷积层后面是池化层时，误差敏感值的传递有所不同。例如，若第l层是卷积层，第l+1层是池化层，那么卷积层的误差敏感值δ可以通过与上采样后的池化层误差敏感值进行点积运算得到。这种关系反映了池化层的局部汇聚特性，其误差会分散到卷积层的相应区域。 上采样（unsample）操作是将池化层的误差敏感值还原到卷积层大小的过程，目的是保持反向传播过程中误差信息的正确传播。例如，在一个4x4的卷积层区域和2x2的池化核下，池化层的一个map的误差敏感值会通过平均池化的逆操作（即上采样）映射回4x4的卷积层区域，确保误差信息在反向传播中被正确分配。 总结起来，卷积神经网络的权值优化涉及到BP算法的扩展和适应，以处理其特有的层间连接和计算方式。理解和掌握这些概念对于构建和训练高效的CNN模型至关重要。