R语言多元线性回归分析：探究牙膏销量与价格差、广告投入关系

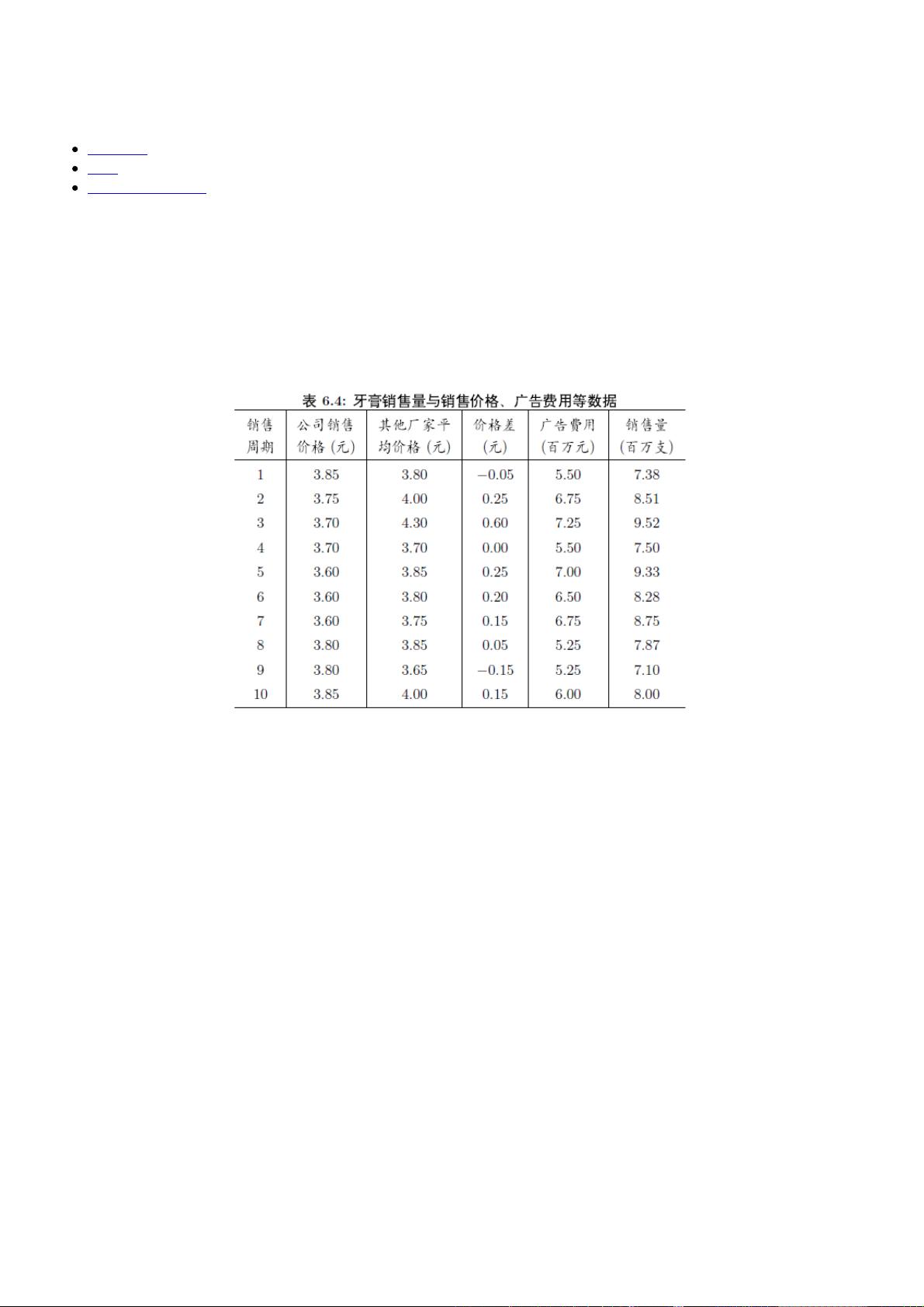
"这篇文档是关于使用R语言进行多元线性回归分析的案例研究，重点关注牙膏销售量与销售价格差异、广告投入之间的关系。案例中，研究人员收集了30个销售周期的数据，包括销售量、价格差异、广告费用和其他厂家平均销售价格。通过R语言的lm()函数构建线性模型，并进行进一步的分析，包括散点图的绘制和模型的改进。最终，通过比较不同模型的残差标准差和多重决定系数，优化了回归模型。" 在R语言中，多元线性回归是一种广泛使用的统计方法，用于研究两个或多个自变量与一个因变量之间的线性关系。在这个案例中，研究的因变量是牙膏的销售量（Y），自变量包括价格差（X1）和广告费（X2）。初步建立的线性模型表示为： \[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \epsilon \] 其中，\(\beta_0\)是截距，\(\beta_1\)和\(\beta_2\)是回归系数，\(\epsilon\)是随机误差项。 在分析过程中，研究人员首先用lm()函数进行回归拟合，并使用summary()函数查看模型的统计信息，如回归系数、显著性水平等。初步模型可能无法完美地捕捉到y与x2之间的关系，因此通过观察散点图，他们决定引入X2的平方项（X2^2），修改模型为： \[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_2^2 + \epsilon \] 这个二次模型提高了模型的解释力，表现为Residual standard error降低，Multiple R-squared上升。然而，对\(\beta_2\)的P-值检查显示其可能不显著，这意味着X2的一次项可能可以剔除。进一步分析后，如果\(\beta_2\)的区间估计包含了0，则表明X2的一次项对模型的影响不明显。 在去掉X2的一次项后，新模型通过了F检验和T检验，但相对于原始模型，Residual standard error的改变表明模型的拟合度可能有所提高。这种优化过程是回归分析中常见的步骤，旨在找到最能解释数据变异性的模型。 通过这个案例，我们可以学到如何在R语言中应用多元线性回归分析解决实际问题，包括数据的预处理、模型构建、结果解释以及模型优化。同时，也展示了如何利用图形工具如散点图来直观理解变量间的关系，并根据统计测试调整模型结构。这个过程对于任何希望使用R进行实证分析的科研工作者或数据分析师来说，都是一个有价值的参考。