2023省一数学建模比赛：多波束测线的建模与优化

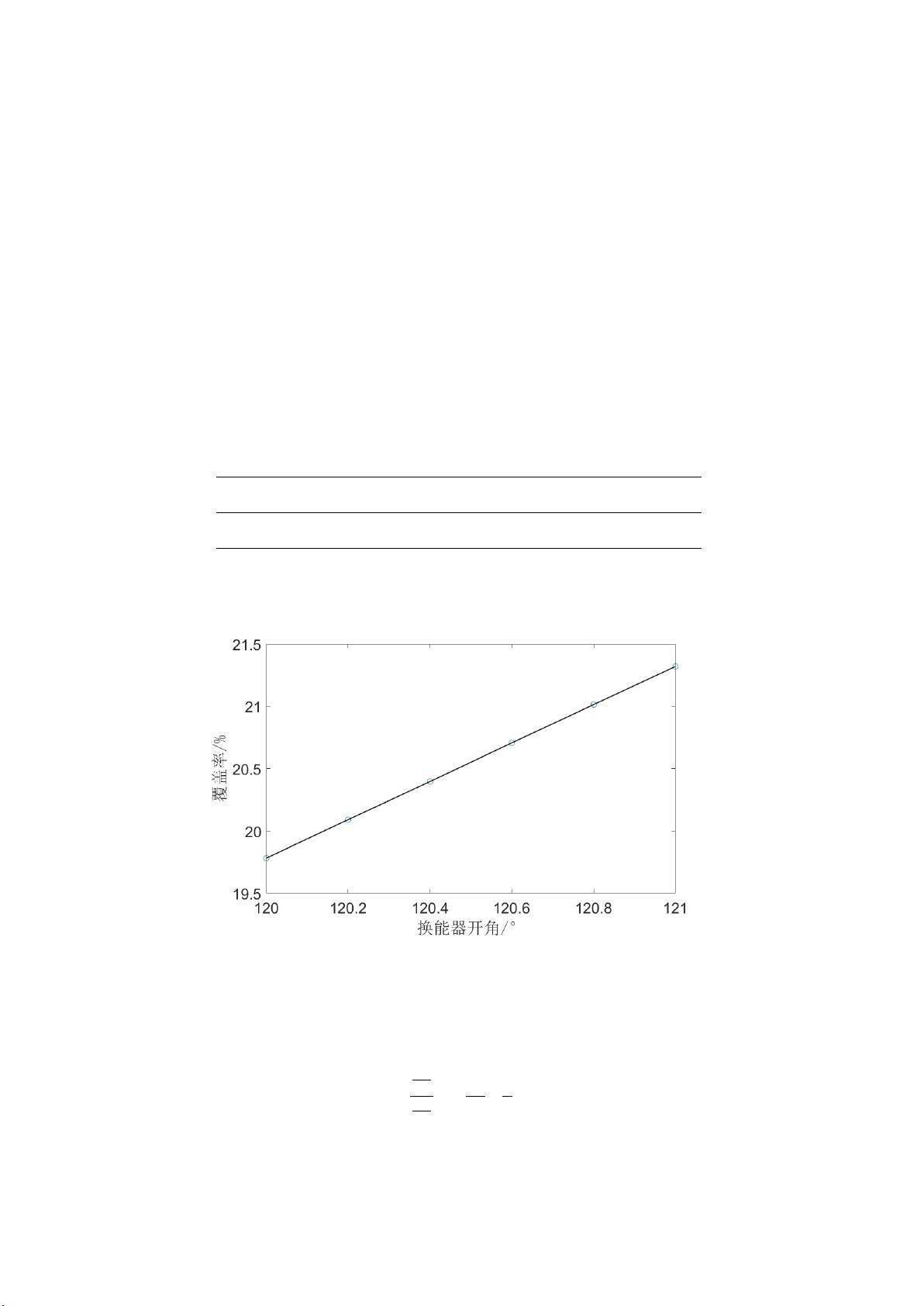
2023年数学建模比赛省一，论文加代码，涉及多波束测线问题。本文针对多波束测线问题，建立了二维几何模型，解决了特定位置下的指标计算问题；建立了三维解析几何模型，完成了特定位置下覆盖宽度的求解；建立了单目标优化模型，给出了最优的测线规划方案；建立了多目标优化模型，给出了最优的多波束测线方案。问题一中，建立了二维几何模型，解决了特定位置下的指标计算问题。首先，以海域中心为原点，以航向垂直的方向为 x 轴，铅直方向为 y 轴建立直角坐标系；其次，求出斜坡直线方程和给定位置处的波束边界方程，进而利用二分法求解波束与斜坡的交点坐标，再由交点坐标实现波束覆盖宽度及相邻条带重叠率的计算。计算结果表明距测线中心-600m处为最大重叠率位置，重叠率为33.64%，此时覆盖宽度为287.59m，距测线中心600m和800m处存在漏测现象，重叠率分别为-1.39%和-11.17%，此时的覆盖宽度为188.53m和170.36m。重叠率对斜坡角度、换能开角和海水深度的灵敏度分析表明：重叠率对海水深度最为灵敏，灵敏度为3.722。最后，利用黄金分割算法对上述结果进行了重新求解，计算结果表明误差都小于0.001，说明计算结果可靠。 本文采用了多种数学建模方法，包括二维几何模型、三维解析几何模型、单目标优化模型和多目标优化模型，成功地解决了多波束测线问题。在二维几何模型中，通过建立坐标系、求解方程和利用二分法等方法，实现了指标计算和覆盖宽度的求解。在三维解析几何模型中，通过对特定位置下的覆盖宽度进行细致分析，得出了相应的结果。而在单目标优化模型和多目标优化模型中，通过分析和优化测线规划方案，得出了最优方案。这些方法的综合应用，充分展示了数学建模在实际问题中的应用价值和解决能力。 此外，本文在计算结果的可靠性方面也进行了充分的分析和验证。通过重新求解和误差分析，验证了计算结果的准确性和可靠性，从而进一步加强了本研究的可信度。 综上所述，本文通过建立多种数学建模方法，成功解决了多波束测线问题，得出了可靠的计算结果和最优方案。这些成果对于实际的海洋测量和勘探具有重要的指导意义和应用价值，为相关领域的研究和实践提供了有力的支持和帮助。同时，本研究也为数学建模在其他领域的应用和拓展提供了有益的经验和借鉴。希望本文的研究成果能够为相关领域的研究者和从业者提供有益的启示和参考，促进相关领域的进一步发展和创新。