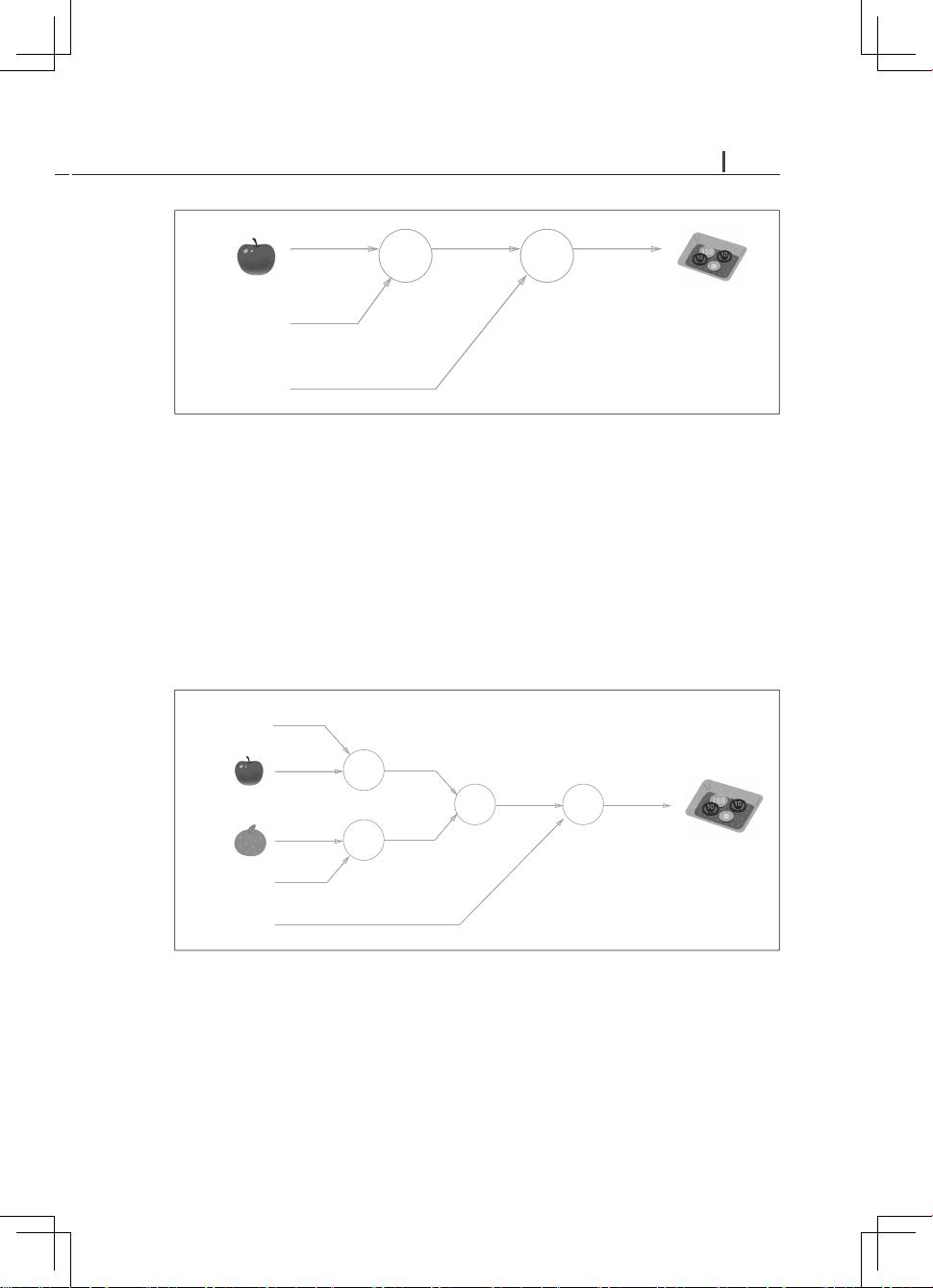
计算图解与多层感知机：异或门的解决方案

本资源主要聚焦于第5章的误差反向传播法，从简单的计算图应用开始，探讨神经网络特别是感知机和多层感知机在解决逻辑问题中的局限性和改进方法。章节首先回顾了感知机，指出了它在实现异或逻辑门时的挑战，因为感知机的线性决策边界无法适应异或函数的非线性特性。异或门无法通过单个感知机表示，因为它的输出取决于输入的两元组是否同时为1，这超出了线性关系的范畴。 2.4节中，作者解释了为何感知机不能实现异或门，通过示例说明感知机的决策边界如何限制其功能。感知机可以用一个直线来区分输出0和输出1的区域，但对异或逻辑来说，这并不适用，因为它需要一个非线性的决策边界，如一个旋转的曲线（如图2-8所示）。 然后，章节转向2.5节，讨论了多层感知机（MLP）的优势，即通过添加隐藏层来构建更复杂的模型，从而能够处理非线性问题。多层结构允许网络学习更复杂的函数，这正是实现异或门的关键所在。这里提到“叠加层”概念，虽然没有深入解释，但暗示了神经网络通过逐层处理输入信息的能力。 4.5节提到了实际的编程实现，使用Python的`TwoLayerNet`类，通过迭代训练过程（例如，`for`循环内的`batch_mask`和`x_batch`、`t_batch`的计算）来更新网络权重，这涉及到梯度计算，这是误差反向传播法的核心，用于调整网络参数以最小化预测错误。 总结起来，这部分内容涵盖了从感知机的局限到多层神经网络的理论提升，以及实际的机器学习算法实现，特别是对于理解误差反向传播在训练深层网络中的作用至关重要。理解这些概念对于理解和应用深度学习技术，特别是在解决非线性问题上，有着重要的基础作用。