Matlab仿真实现：一阶倒立摆控制系统设计与分析

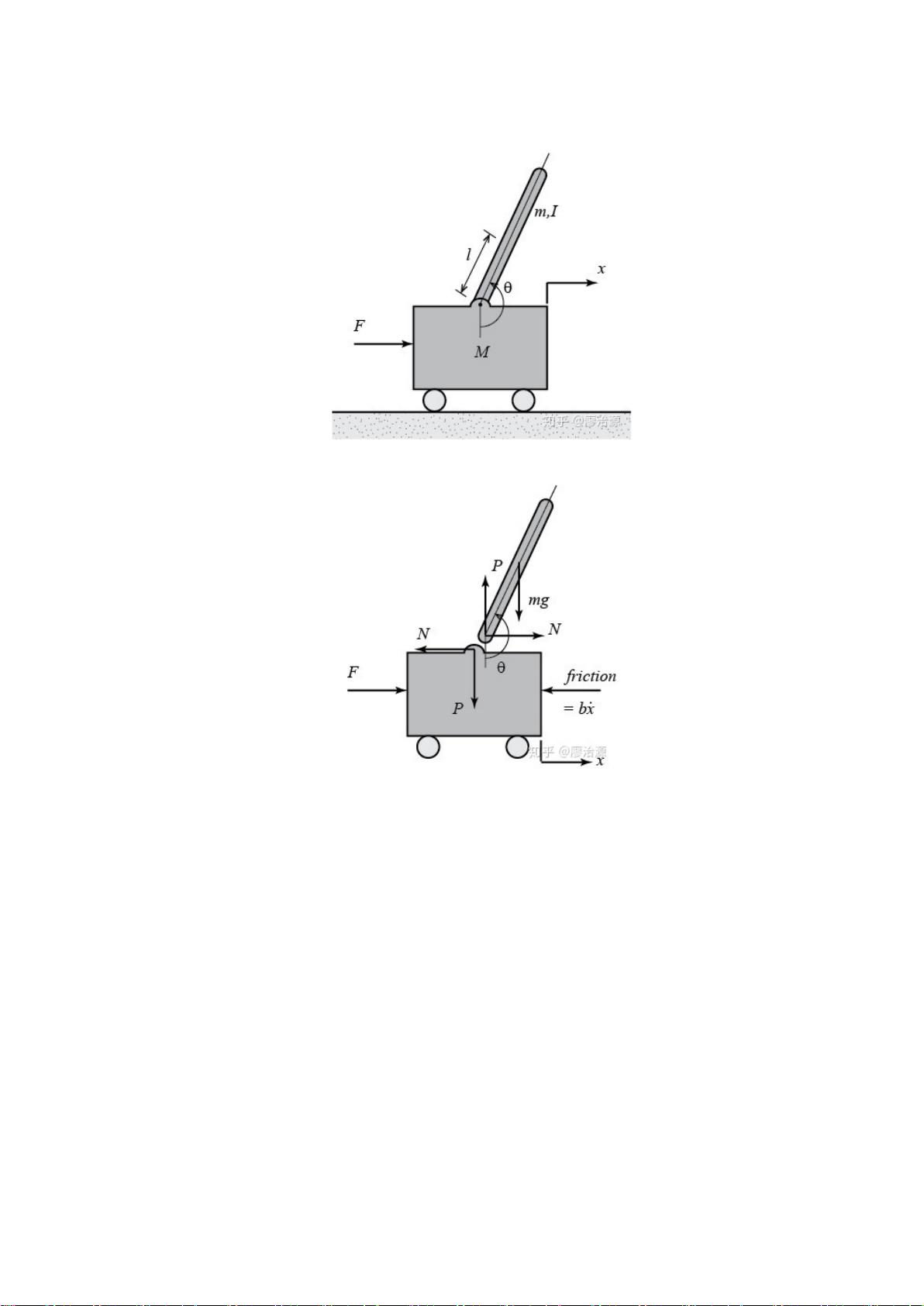
本文档详细介绍了如何利用MATLAB软件进行一阶倒立摆的数学模型建立和SIMULINK多体动力学平台上的控制系统仿真。首先，我们关注的是一个由小车和倒立摆构成的控制系统，系统参数包括小车质量M=0.5kg，摆杆质量m=0.2kg，摆杆长度2l=0.6m，以及小车的摩擦系数b=0.1N/(m/s)。此外，系统的转动惯量I=ml^2/3=0.006 kg*m^2，这对于后续的动态分析至关重要。 在系统建模部分，作者分别考虑了小车和摆杆的动力学方程。小车受到重力、摩擦力和施加的力F的作用，其运动方程可以表示为牛顿第二定律，而摆杆的运动则涉及到关节力矩N和P，它们与摆杆的角度θ和角速度有关。通过代数运算，得到了x（小车位置）和θ（摆杆角度）关于力F的表达式，并通过三角恒等变换简化了方程组。 为了进一步分析，作者将摆杆角度θ表示为φ+π，这样当φ在0附近变化时，简化了数学处理。通过拉普拉斯变换，原始的微分方程组被转换成便于分析的频域表达式，从而形成了系统的简化框图。框图中包含了输入F、系统函数G(s)、状态变量X(s)等重要元素。 最终，文档展示了系统的阶跃响应，其中蓝色线代表位置响应，黄色线可能代表角度响应，这是评估控制器性能的重要指标。通过这种仿真方法，研究者可以观察到不同控制策略下倒立摆的动态行为，优化控制器的设计，以实现对小车位置和摆杆角度的精确控制。 总结来说，本论文的核心内容是运用MATLAB的SIMULINK工具箱来模拟和分析一阶倒立摆的动态特性，涉及了从物理模型建立、数学建模到系统仿真的一系列步骤，这对于理解倒立摆的运动规律以及设计有效的控制策略具有重要意义。