C语言实现高精度乘法：列表法与算法详解

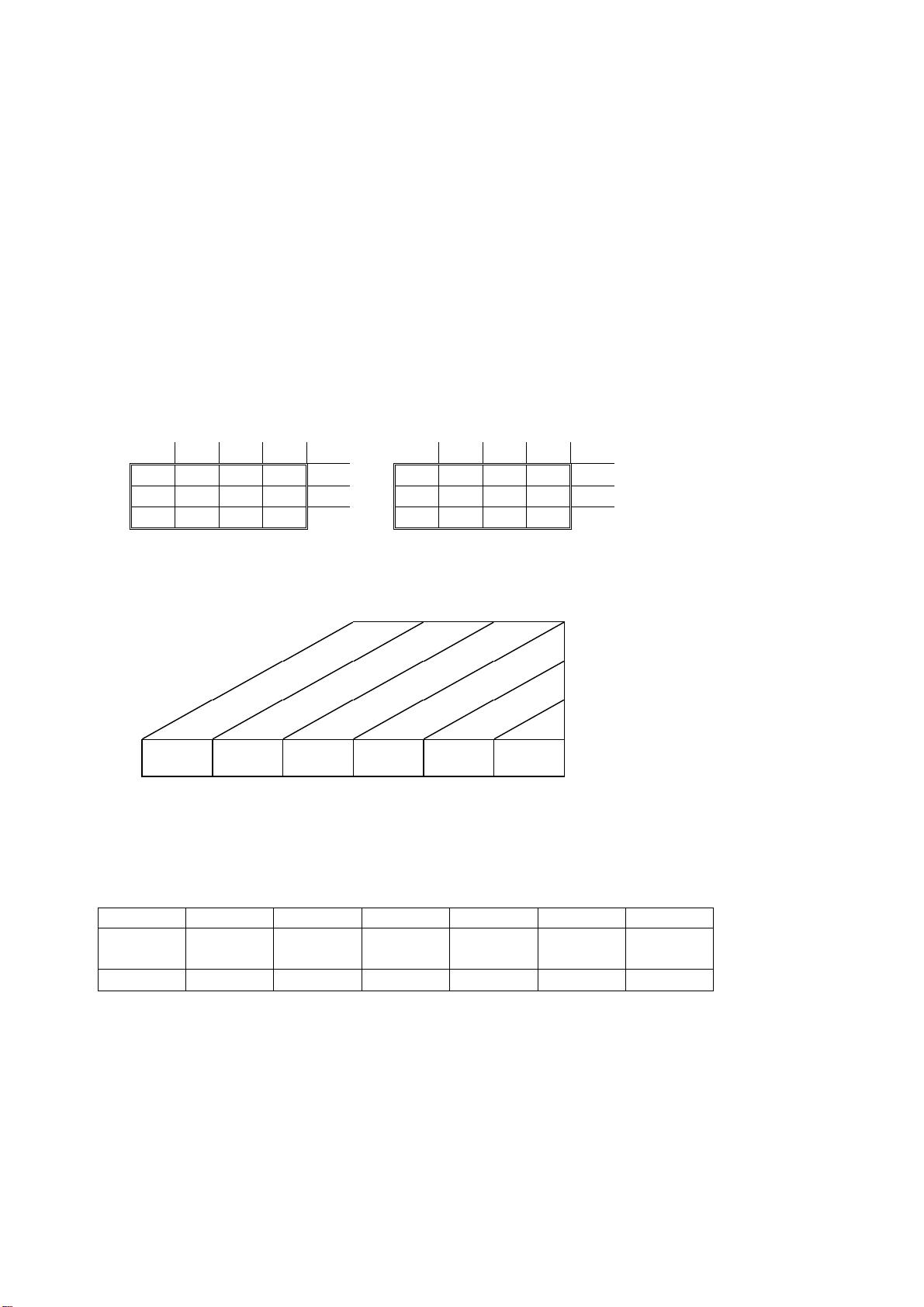
高精度运算在C语言中是一项重要的任务，特别是当涉及到大整数乘法时，由于标准数据类型（如longint和double）的精度有限，可能无法满足需要精确到数十位甚至更多的数值计算。本文讨论了如何通过列表法来实现大整数的乘法运算，这种方法能够避免溢出问题并提供更高的精度。 首先，列表法的基本原理是将乘数和被乘数按照竖式计算的方式分解成多行和多列，然后逐个计算这些位置上的乘积，并按照固定的规则进行进位。具体步骤如下： 1. **分解乘数和被乘数**：将两个待乘的整数转换为多位数的形式，例如8765和234。 2. **填充乘法表**：创建一个二维数组，每个元素表示相应位置的乘积，如表1所示。 3. **累加进位**：按照斜线将乘积数组划分为若干组，对每组求和，并在必要时进行进位操作，例如表3和表4。 4. **处理结果**：从最低位开始，依次将进位添加到前面的数位，直到得到最终的乘积。 5. **算法复杂性**：对于一个m位乘n位的整数，乘积的位数将是m+n-1或m+n，这表明需要预先为乘积数组分配足够的空间，至少是两个输入数位数之和。 在编程实现时，关键在于设计两层嵌套循环结构：外层循环控制行数（乘数），内层循环负责计算和进位操作。此外，可以考虑合并“计算填表”和“累加进位”的步骤，以减少存储需求。 以下是一个简化的C语言代码片段，展示了如何使用列表法实现高精度乘法： ```c #include <stdio.h> #include <string.h> // 函数声明 char* multiply(char* num1, char* num2, int len1, int len2); // 主函数 int main() { char num1[] = "8765"; char num2[] = "234"; int len1 = strlen(num1); int len2 = strlen(num2); char* result = multiply(num1, num2, len1, len2); printf("乘积: %s\n", result); free(result); return 0; } // 列表法乘法函数 char* multiply(char* num1, char* num2, int len1, int len2) { int sum_len = len1 + len2 - 1; // 预计乘积位数 char* product = (char*)malloc(sum_len + 1); // 为进位预留一位 // 填充乘法表 for (int i = 0; i < len1; ++i) { for (int j = 0; j < len2; ++j) { product[i + j] += (num1[i] - '0') * (num2[j] - '0'); } } // 进位处理 for (int i = 1; i < sum_len; ++i) { product[i] += product[i - 1] / 10; product[i - 1] %= 10; } // 添加前导零（如果不足位数） if (product[sum_len] == 0) { --sum_len; } product[sum_len] = '\0'; // 结束符 return product; } ``` 这段代码展示了如何运用列表法实现大整数乘法，注意在实际应用中，可能需要进一步优化内存管理和错误处理，确保程序的健壮性。