Python递归实战：斐波那契数列与汉诺塔问题

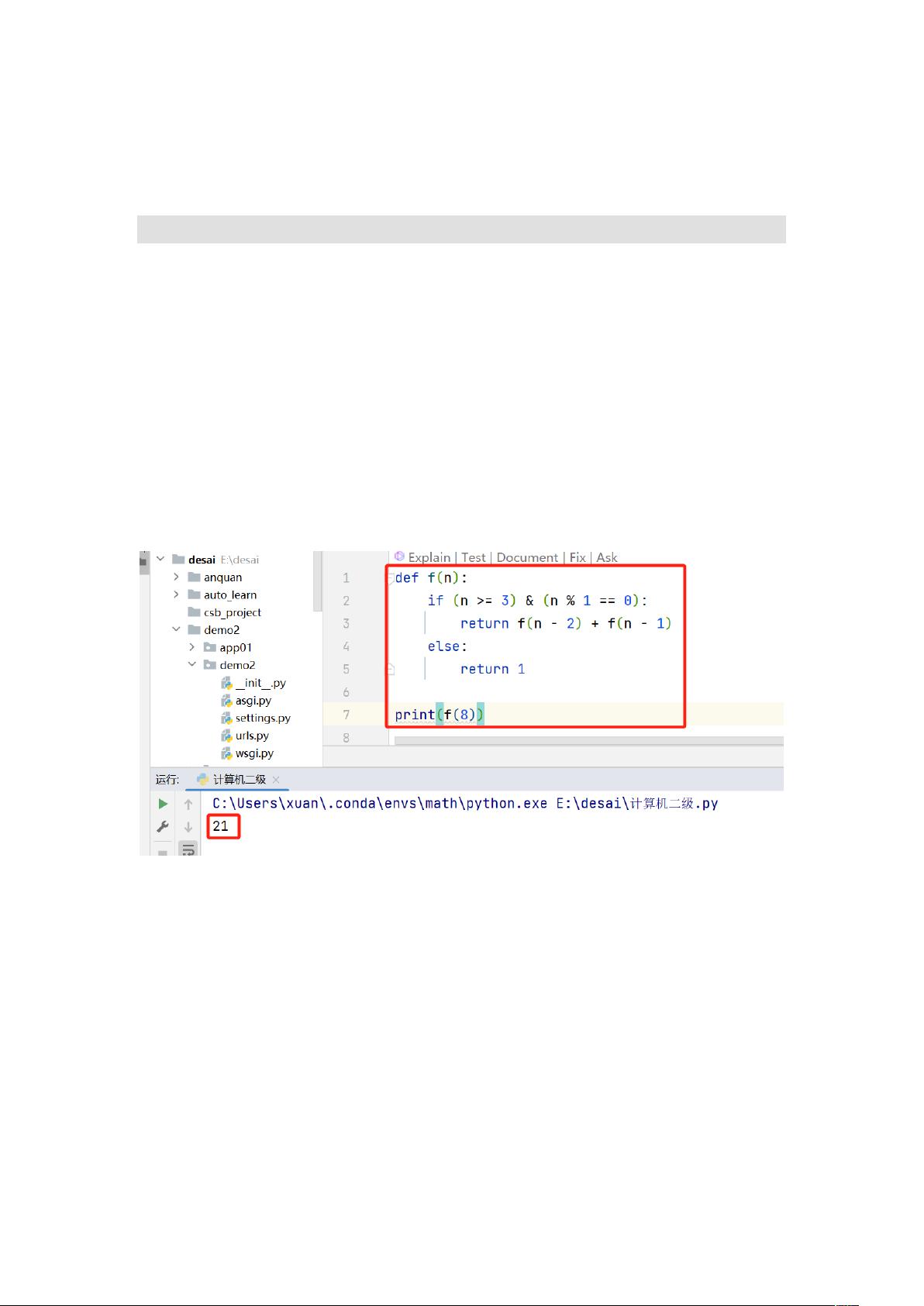
在Python编程中，递归算法是一种强大的工具，它通过函数调用自身来解决问题。本篇练习主要涉及两个经典的递归问题：斐波那契数列和汉诺塔问题。 斐波那契数列 斐波那契数列是自然数列中的一串数字，每个数字是前两个数字之和，起始两项为1。在任务一中，要求编写一个递归函数`fibonacci(n)`，实现根据用户输入的整数`n`计算第`n`个斐波那契数。递归函数的边界条件是当`n`等于1或2时，直接返回相应的值；对于较大的`n`，则遵循递归公式`F(n) = F(n-1) + F(n-2)`。编写递归函数的关键在于理解并处理好这两个基础情况和递归调用。 汉诺塔问题 汉诺塔是一个经典的递归问题，源于一个关于黄金圆盘的移动挑战。任务二是将一个有`n`个圆盘的塔从柱子A移动到柱子C，但每次只能移动一个圆盘，并且任何时候小圆盘都不能位于大圆盘之上。递归解决此问题的策略是将问题分解为更小的子问题，比如将前`n-1`个圆盘从A移动到B，然后将最大的圆盘从A移动到C，最后再将剩下的圆盘从B移动到C。递归函数的边界条件是当只有1个圆盘时，直接进行一次移动；递归公式则是根据子问题的解决策略来设计函数。 总结来说，这两个任务旨在帮助学习者理解递归的基本概念，包括明确递归函数的边界条件（最小规模的可解情况）和递归公式（如何将问题分解为规模更小的子问题），以及如何在Python中实际编写和执行递归函数。通过这两个实践，学生可以提高对递归算法的理解，掌握如何将其应用到实际问题中，从而提升编程技能。