数据结构：树与二叉树详解 - 逻辑结构、度与层次特性

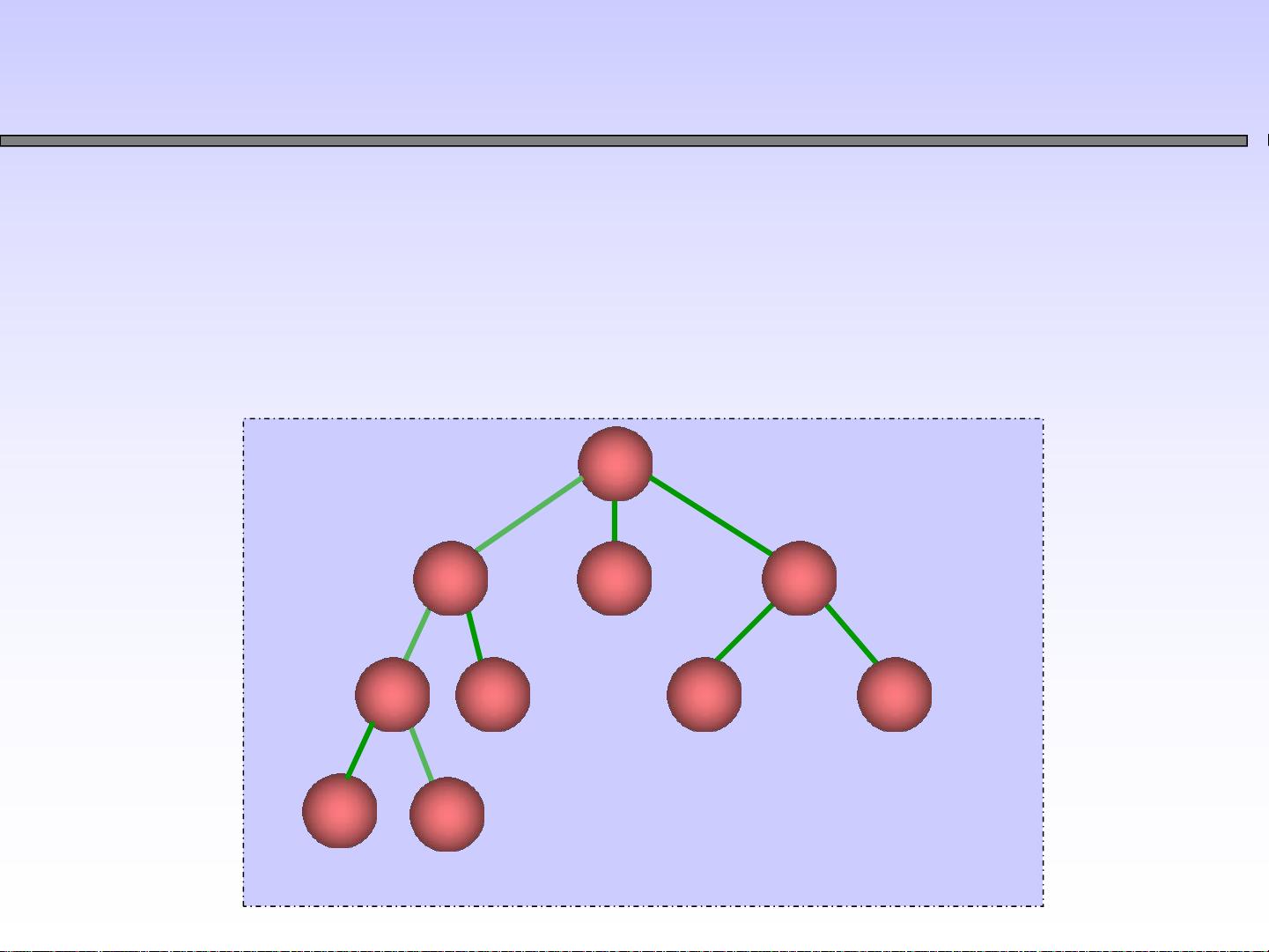
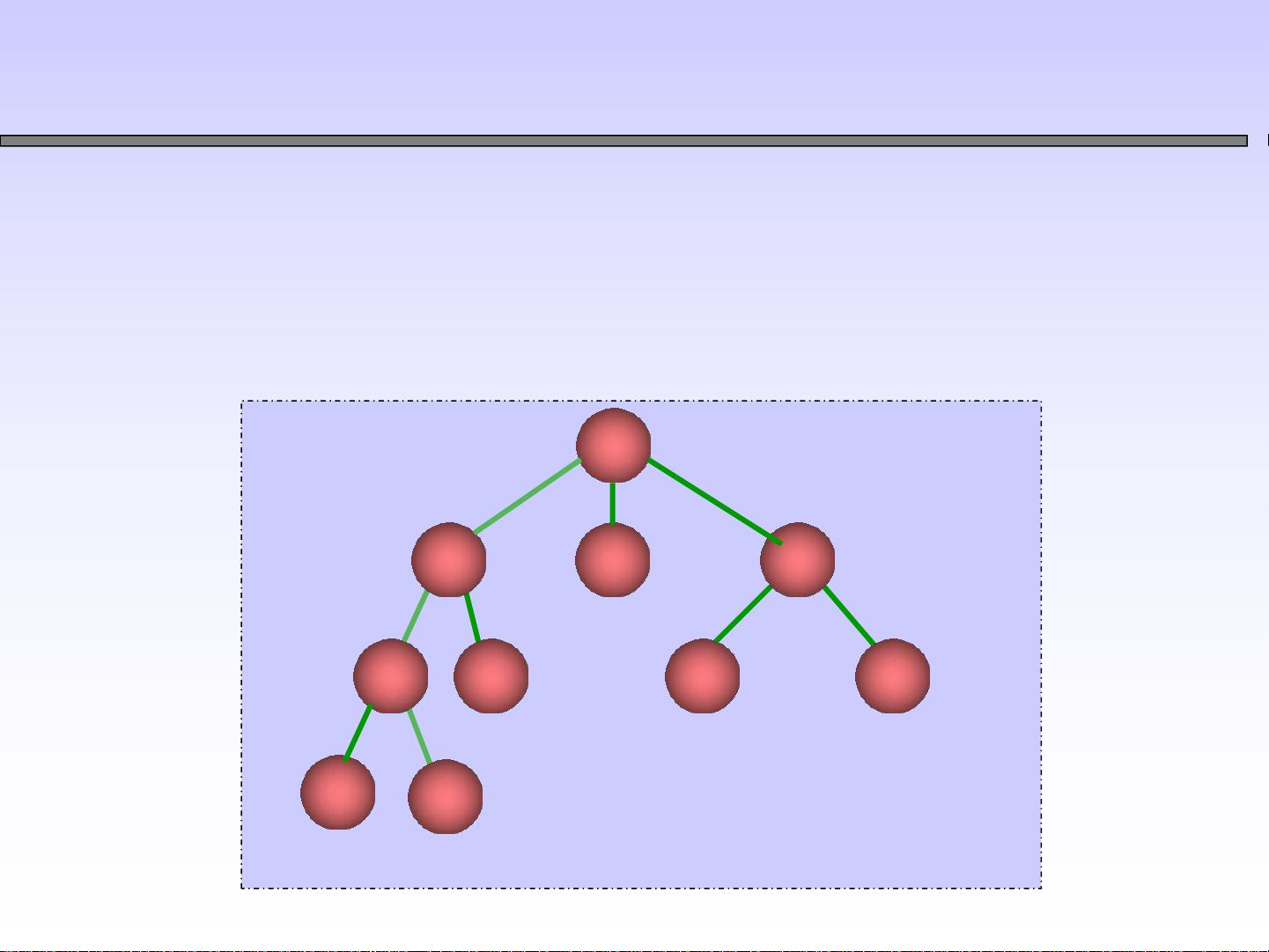
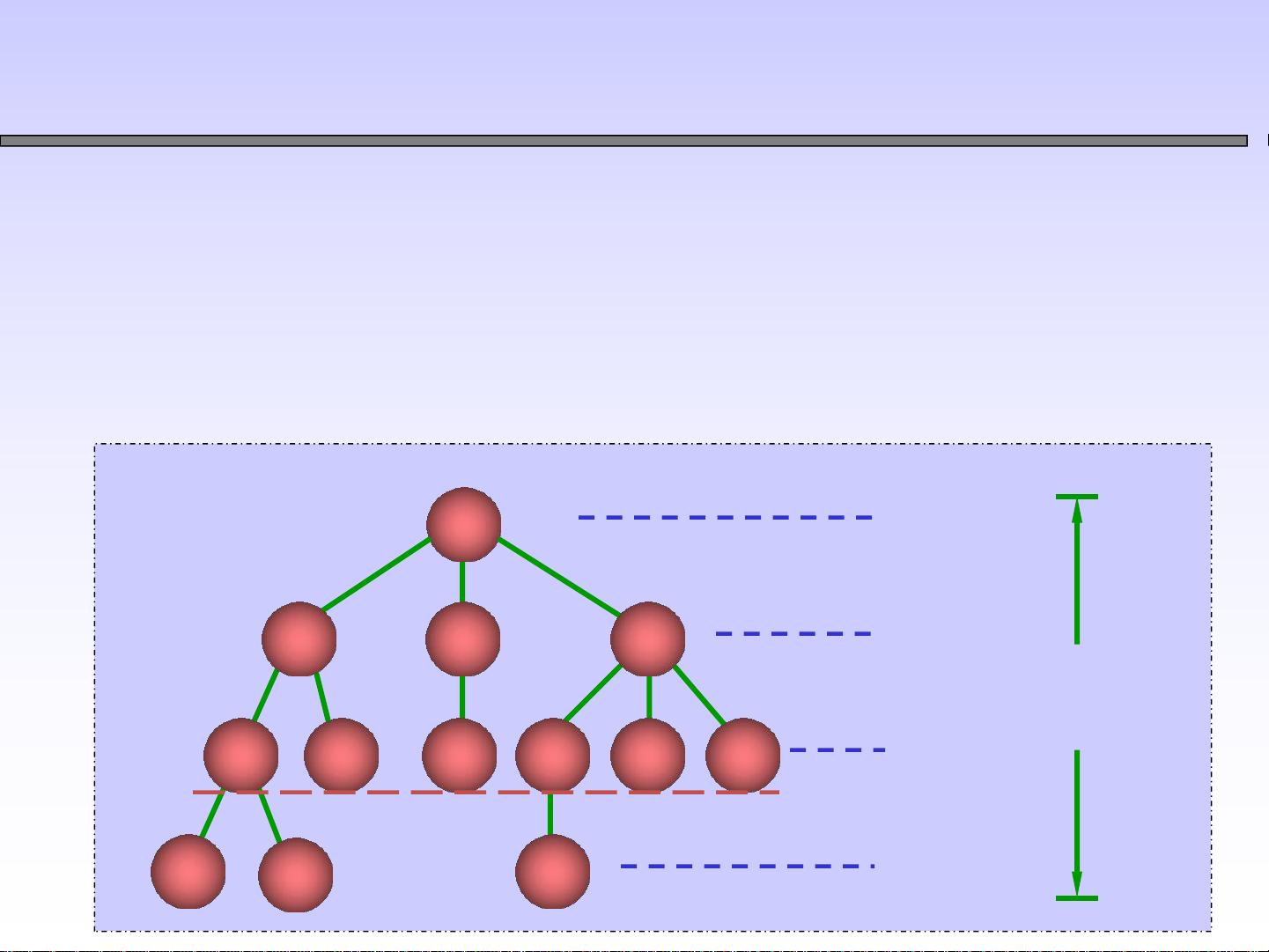
第5章"树和二叉树"是关于数据结构中的重要概念，主要探讨了树的理论基础及其在实际应用中的体现。树是一种非线性数据结构，其逻辑结构通过递归定义，具有层次性和互不相交的特性，确保了结构的清晰和无环。以下是本章的核心知识点： 1. 树的定义： - 树由n个结点组成，当n=0时为空树；非空树有一个特殊的根结点，其余结点被划分为若干互不相交的子树，每个子树本身也是一个树。 2. 树的逻辑结构： - 采用递归方法来描述，如例3所示，树的逻辑结构强调了结点间的层次关系，如文件系统中的目录结构或表达式树的运算符和操作数的层次表示。 - 互不相交的特性意味着每个结点只能属于一个子树，且子树间不存在共享边或回路，这保证了树的唯一性。 3. 树的术语： - 度：一个结点的度是其子树数量，表示该结点的分支能力。树的度是所有结点度的最大值。 - 叶子结点（终端结点）：度为0的结点，没有子树。 - 分支结点（非终端结点）：度不为0的结点，至少有一个子树。 4. 二叉树： - 一种特殊的树，每个结点最多有两个子结点，通常用于更紧凑的存储和处理，如哈夫曼树（一种带权路径长度最短的二叉树）。 5. 存储结构和实现： - 二叉树的存储方式有多种，如顺序存储、链接存储等，需要考虑如何有效地访问和操作结点。 6. 树与二叉树的转换： - 如何在不同的数据结构之间转换，例如将一般树转换为二叉树，或者利用哈夫曼树进行数据压缩编码。 7. 实际应用： - 文件系统，如操作系统中的文件夹结构，体现了树的层次关系。 - 表达式树：通过后序遍历将算术表达式转化为逆波兰式，便于计算。 - 计算机系统中的各种数据组织，如内存管理或进程调度。 8. 哈夫曼树和哈夫曼编码： - 哈夫曼树是一种构建最优二叉树的方法，用于数据压缩，特别是文本编码，如ASCII码。 第5章深入讲解了树和二叉树的理论概念、重要术语以及它们在实际问题中的应用，对于理解数据结构和算法设计具有重要意义。