Monte Carlo方法解析：从历史到数值积分

"本文档介绍了Monte Carlo算法的基本概念、历史背景、以及其在数值积分中的应用。通过大量随机试验，Monte Carlo方法利用概率论解决复杂问题，区别于仅模拟随机过程的Simulation。该方法在20世纪40年代因原子弹计划中的模拟需求而得名，并广泛应用于各种领域，尤其是数值积分。文中通过举例说明了Monte Carlo数值积分的原理和优势，即通过随机点的分布来近似求解复杂函数的积分，随着试验次数的增加，结果的精度提高。" 在数学和计算机科学中，Monte Carlo算法是一种强大的工具，尤其在处理高维度和复杂问题时，它展现出了高效性。该方法的核心在于通过随机抽样来求解问题，而不是依赖解析解或传统数值方法。Monte Carlo方法的历史可以追溯到18世纪，其中布丰的投针实验是早期的实例，用于估算圆周率。然而，这个名字直到20世纪40年代才被正式赋予，与核物理研究有关。 在数值积分方面，当函数f(x)过于复杂，无法找到原函数F(x)时，Monte Carlo方法提供了一种有效的方法。传统的数值积分技术，如梯形法则或辛普森法则，通过将积分区间分割并计算每个小段的近似面积来求和。相比之下，Monte Carlo方法更侧重于随机性。它在积分区间内随机生成大量点，然后统计这些点位于函数f(x)上方的比例。这个比例近似于函数图形与x轴所围区域的面积占总面积的比例，从而估计出积分的值。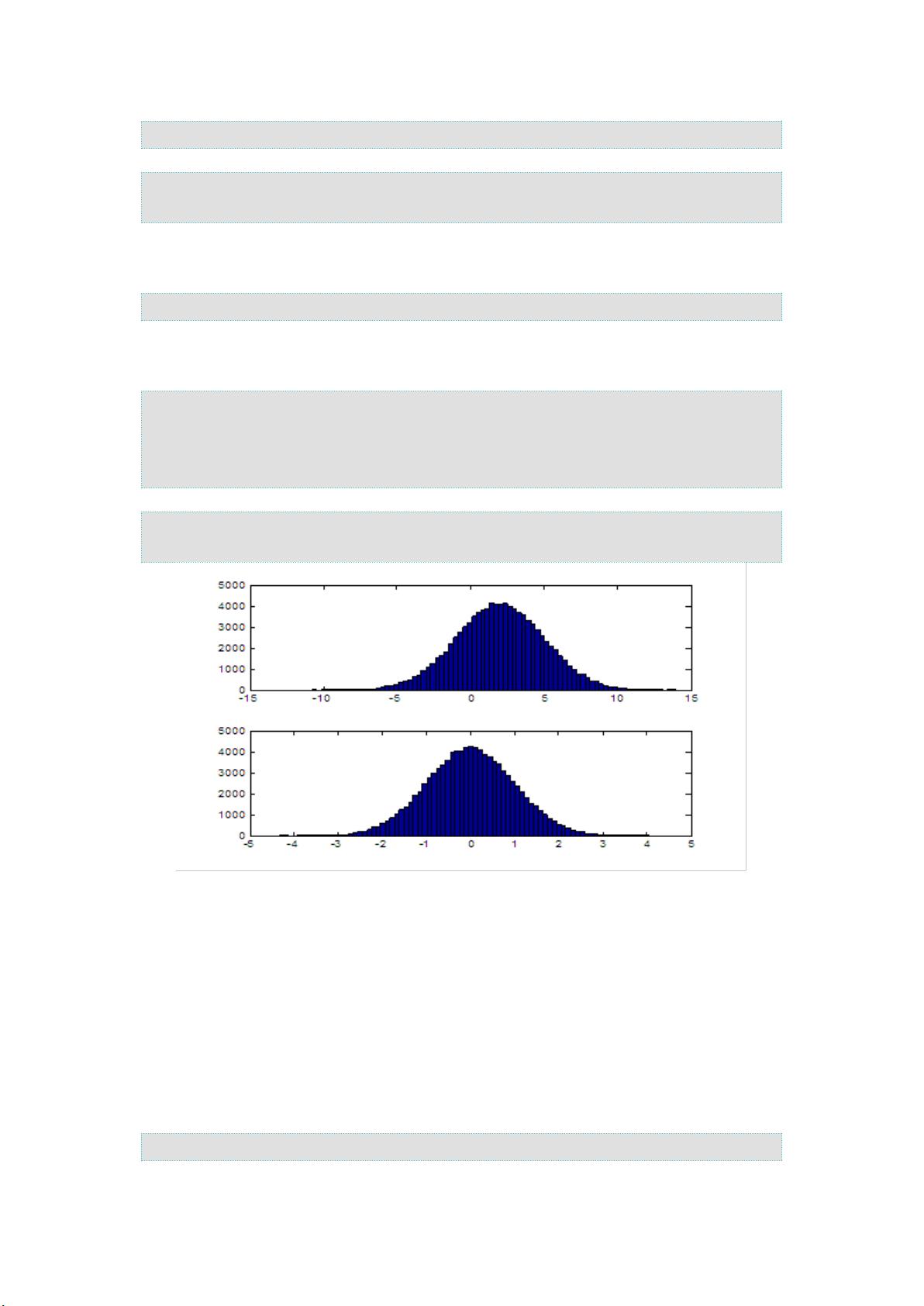 例如，对于一个简单的数值积分，我们可以将区间分为若干段，用矩形面积近似函数的曲线面积。在Monte Carlo方法中，我们不再关心这些矩形，而是随机生成大量点，计算这些点落在函数图像上方的数量。这个数量除以总点数，乘以区间面积，就得到了积分的估计值。随着随机点的数量增加，这个估计值会越来越接近真实的积分值，体现了Monte Carlo方法的收敛性。 除了数值积分，Monte Carlo方法还广泛应用于统计物理、金融建模、机器学习、优化问题、模拟和预测等多个领域。其灵活性和适应性使其成为解决现实世界复杂问题的重要手段。通过掌握Monte Carlo算法，我们可以解决那些传统方法难以触及的问题，特别是在数据和计算资源有限的情况下。在MATLAB这样的环境中，实现Monte Carlo算法非常便捷，使得科研和工程人员能够快速原型验证和优化解决方案。 Monte Carlo方法是一种强大的数值计算方法，通过随机抽样和概率论原理，解决了许多其他方法难以处理的问题。尽管其结果依赖于随机过程，但最终的解却是确定且具有可靠性的。随着计算能力的不断提升，Monte Carlo方法的应用将更加广泛，继续在各个科学和工程领域发挥重要作用。