MATLAB实现的非线性方程求解：二分法与黄金分割法

"第二章 基于MATLAB的科学计算-非线性方程(组)" 本章节主要探讨了如何使用MATLAB进行科学计算，特别是处理非线性方程的求解方法。非线性方程的求解在工程、物理、数学等多个领域都具有重要意义，因为许多实际问题往往不能简化为线性形式。本文主要介绍了两种经典方法：二分法和黄金分割法。 首先，二分法是一种基于连续函数介值定理的求解方法，适用于求解单根的非线性方程。它假设方程在闭区间[a, b]上存在唯一解，并且f(a) * f(b) < 0，即函数值在区间两端异号。例如，给定方程f(x) = x^3 - 2.3x^2 + x*sin(x) + 0.3，通过MATLAB的plot函数可以绘制函数图像，确认该方程在区间[1, 2]有一个根。二分法的基本步骤是不断将包含根的区间分为两半，通过比较中点处的函数值与零的关系来判断根所在的子区间，直至达到预定的精度要求。其收敛速度是线性的，二分次数N可以通过公式N ≥ log2(1/ε)估算，其中ε是所需的精度。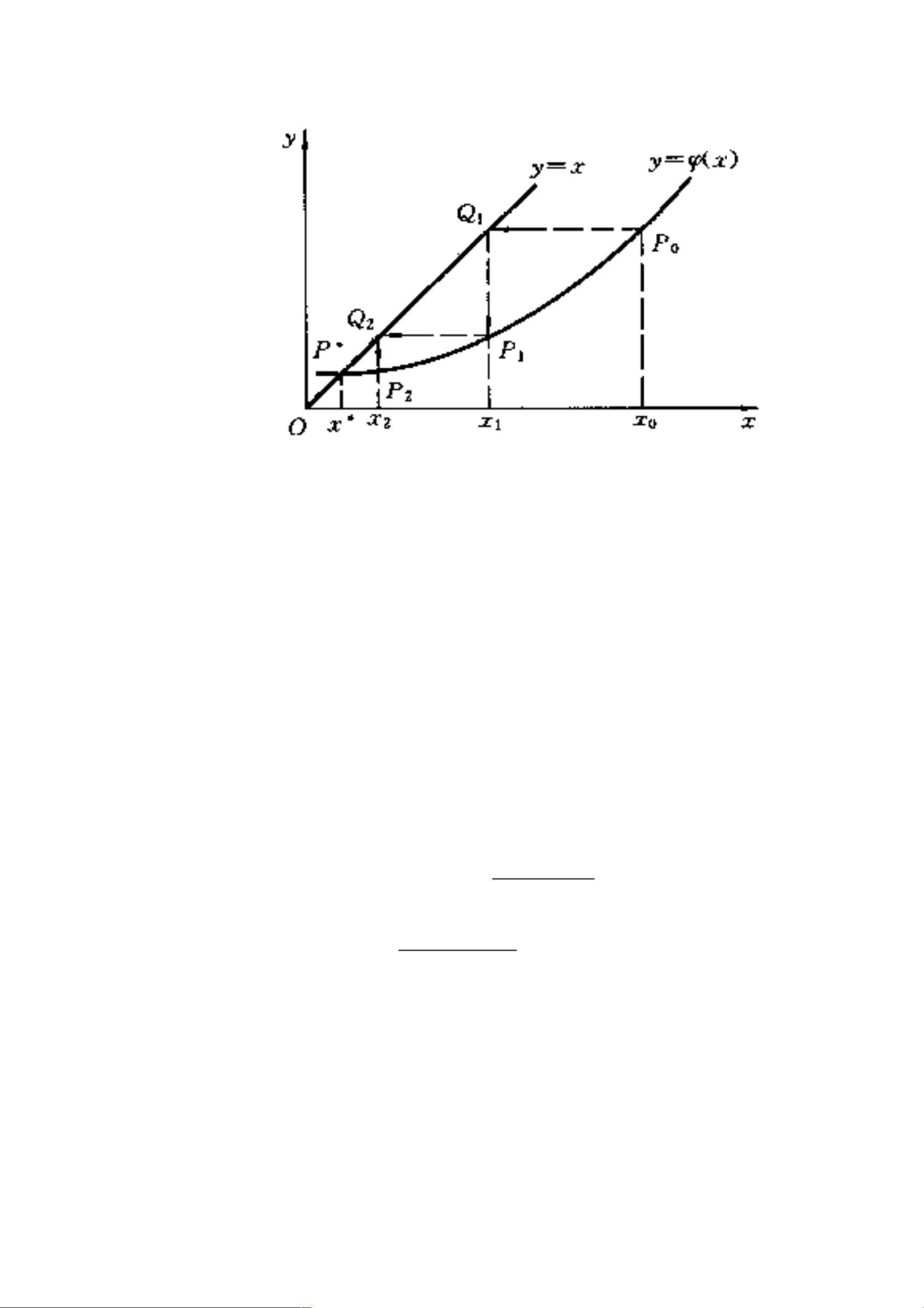 其次，黄金分割法是另一种非线性方程求解策略，它在每次迭代时选择更接近根的区间，相比二分法通常能更快地收敛。在区间[a, b]内，黄金分割法选取两个点x_a和x_b，它们的比值是黄金分割比（1-√5）/ 2，即x_a = a + (1-β)(b-a)，x_b = a + (b-a)/2，其中β是黄金分割比例的倒数。这种方法的优点在于，即使初始区间不是最佳选择，也能保证较快收敛。 在MATLAB中，实现这些算法通常涉及到循环结构和条件判断，以及函数值的计算。例如，可以编写一个MATLAB脚本来实现二分法，包括设定初始区间、精度阈值ε，以及循环迭代直到找到满足精度的根。 非线性方程的求解是MATLAB科学计算中的一个重要部分，二分法和黄金分割法提供了两种实用的数值方法。在实际应用中，可以根据问题的具体特点和计算效率需求来选择合适的方法。通过MATLAB强大的图形界面和编程环境，可以方便地进行非线性方程的数值求解，并对结果进行可视化验证。