模糊数学应用：三角模糊神经网络预测解析

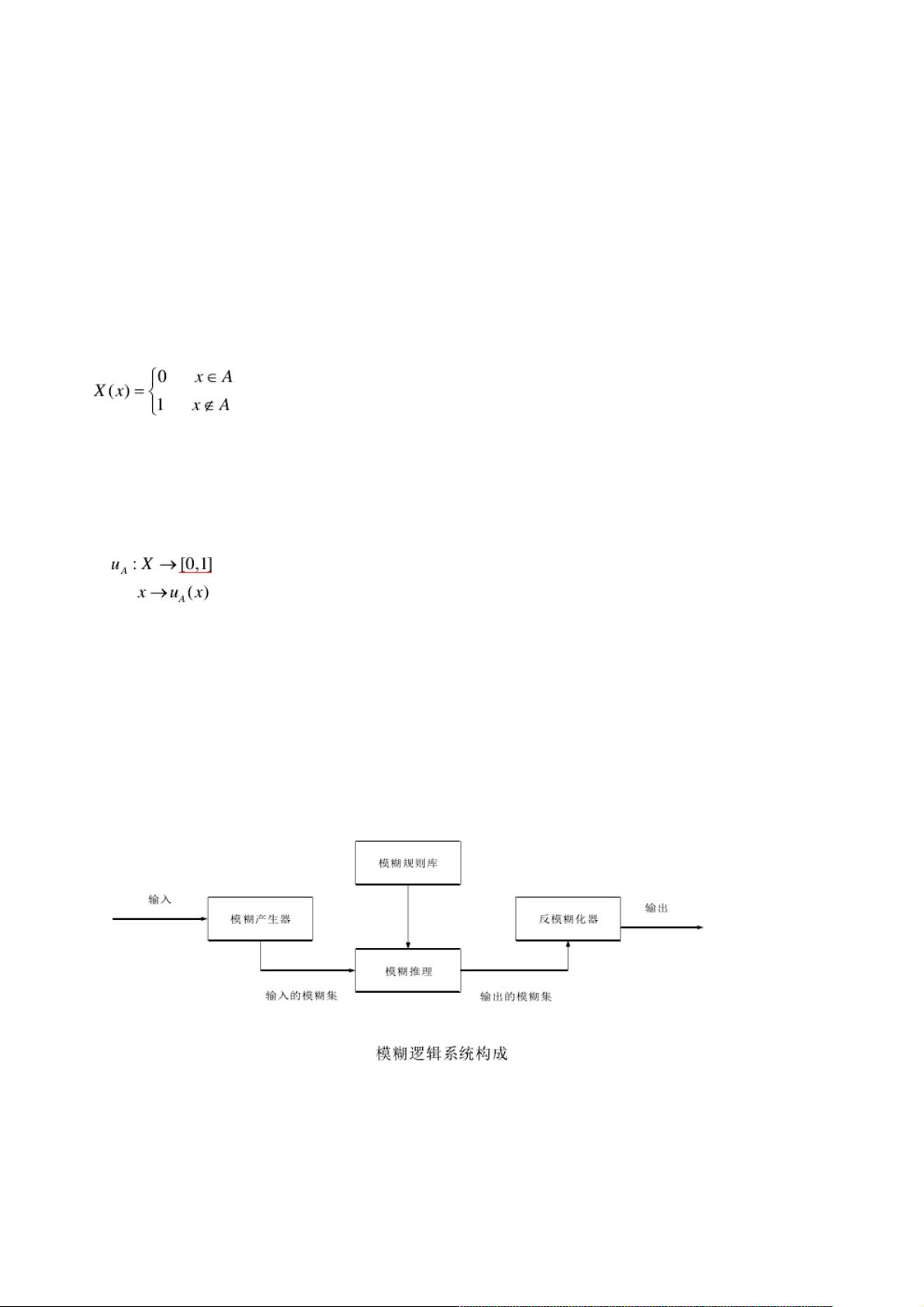
"三角模糊神经网络的预测" 模糊理论是一种数学工具，用于处理现实生活中的模糊现象，即那些界限不清、难以精确定义的概念。1965年，Lotfi Zadeh提出了模糊集合的概念，将传统的二元集合论扩展到连续的隶属度函数，允许元素对集合的隶属程度介于0到1之间，从而更好地描述了现实世界中的模糊性。模糊集合的隶属函数值越接近1，表示元素对集合的归属越明确；反之，接近0则表示归属不明确。 模糊逻辑系统是基于模糊集合和模糊推理的系统，通常包括模糊产生器、模糊规则库、模糊推理机和反模糊化器。模糊产生器将输入转换为模糊子集，模糊规则库存储一系列模糊规则，模糊推理通过这些规则进行推理，而反模糊化器则负责将模糊输出转化为实际可操作的数值。 在模糊系统中，隶属函数起着关键作用。常见的隶属函数类型有三角形和梯形函数，它们能够灵活地刻画不同模糊概念的连续变化。三角隶属函数特别适合描述在一定范围内连续变化的模糊属性，如温度或年龄。 三角模糊神经网络是结合模糊理论和神经网络的一种模型。神经网络是一种模仿生物神经系统的计算模型，由大量简单的处理单元（神经元）构成，具有并行处理、自我学习和强纠错能力。将模糊逻辑与神经网络结合，可以提高模型对模糊数据的处理能力和预测精度，特别是在处理不确定性问题时，如经济预测、医疗诊断、控制系统等。 BP（Backpropagation）神经网络是神经网络的一种，以其反向传播算法闻名。在训练过程中，BP神经网络通过调整连接权重来优化网络性能，使其能够从输入数据中学习并适应复杂的模式。当应用于模糊神经网络时，BP算法可以帮助模糊系统更有效地学习和调整模糊规则，以适应模糊输入，并产生精确的输出。 总结来说，三角模糊神经网络是融合了模糊理论和神经网络技术的预测模型，它利用三角形隶属函数处理模糊数据，并借助BP算法进行训练和优化，从而在不确定性和模糊性较高的问题上展现出强大的预测能力。这一方法在众多领域，如工程、经济、医学等，都展现出了广泛的应用前景。