MATLAB符号工具箱：连续信号傅立叶变换与符号运算详解

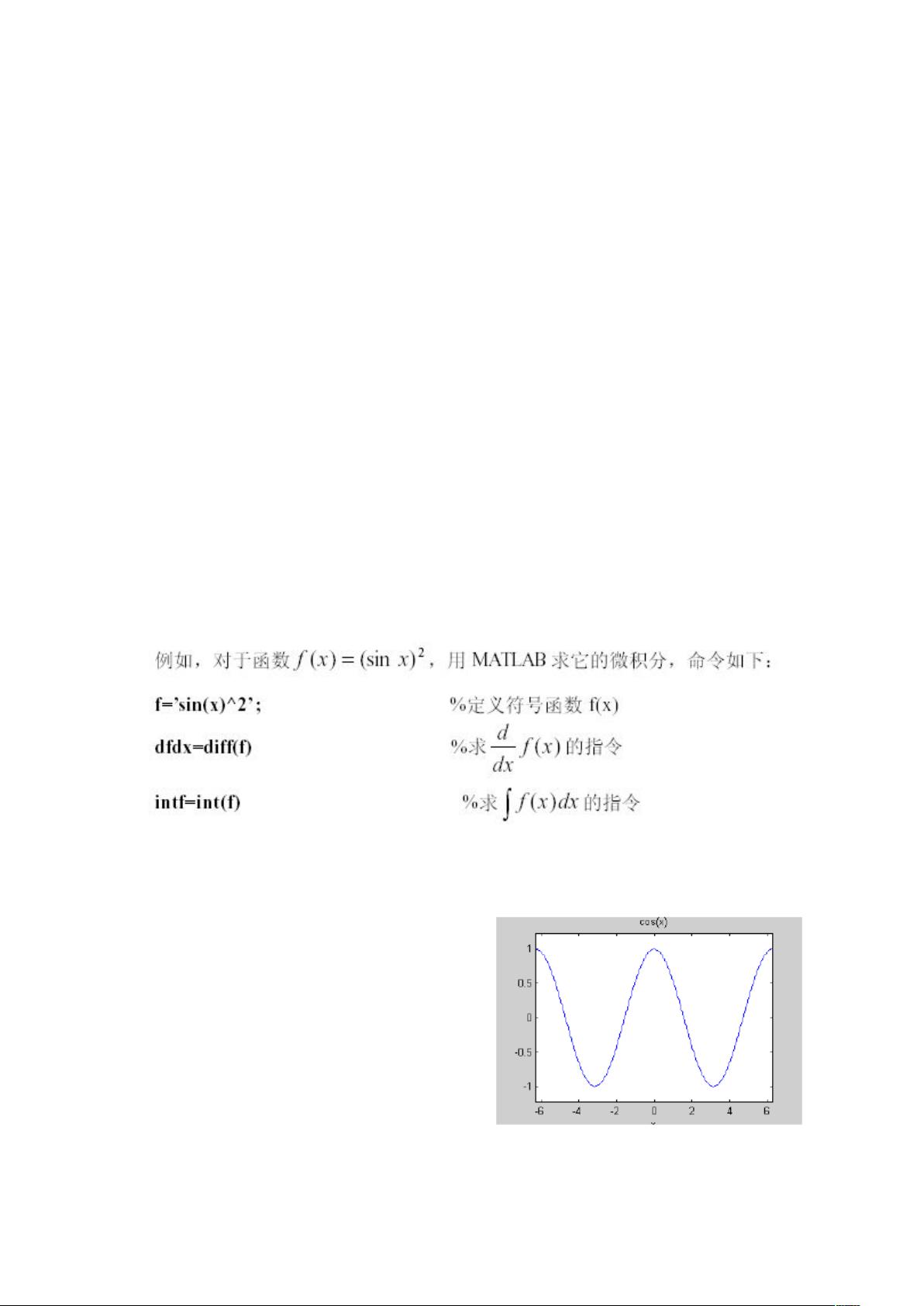
连续信号的傅立叶变换是信号处理中的重要概念，它描述了时间域中的信号如何在频域中表示。在MATLAB的Symbolic Math Toolbox中，这一理论得到了实用化的应用，通过符号对象（Symbolic object，简称sym）的数据类型，可以方便地处理符号变量、表达式和矩阵。 首先，要使用MATLAB进行符号运算，需要先声明符号变量。这可以通过`syms`函数完成，例如`syms x a`或者`x = sym('x'); a = sym('alpha')`，这些变量会被定义为符号类型，支持复杂的数学运算。 MATLAB提供了直观的绘图工具`ezplot()`，用于绘制符号函数。其基本用法是`ezplot(f)`，会根据默认范围`-2*pi < x < 2*pi`绘制函数f(x)。更具体的是，可以指定自定义的x轴范围，如`ezplot(f, [xmin, xmax, ymin, ymax])`。 符号变量替换也是符号计算中的关键操作，`subs()`函数允许用户用新变量替换旧变量。例如，`subs(f, 'a', 2)`将把符号表达式f中的'a'替换为2，输出结果为`sin(1/3*2*pi)`。 在进行数学分析时，`diff()`函数用于对符号表达式求导，如`syms a x; f = sin(a*x); df = diff(f)`，得到的结果是f关于x的导数。类似地，`int()`函数用于求不定积分，如`syms x; s = '1/(1+x^2)'; f = int(s)`，得到的结果是函数`s`的原函数`f = atan(x)`。 对于周期信号，傅立叶级数分解与综合是典型的应用。由于周期信号可能包含无限个非零的傅里叶系数，实际操作中通常需要对信号进行截断，只考虑有限项。在MATLAB中，利用符号计算工具处理周期信号的傅立叶级数有助于深入理解信号的频率成分。 通过MATLAB的符号运算功能，不仅能够直观地表示和分析连续信号，还能进行数值计算，这对于理论研究和工程实践中的信号处理问题具有极大的便利性。掌握这些工具和技术，有助于我们更好地理解和处理复杂的信号系统。