黎曼几何与数学物理入门：曲面、Lie群与哈密顿系统

需积分: 9 192 浏览量更新于2024-07-18 收藏 7.48MB PDF 举报

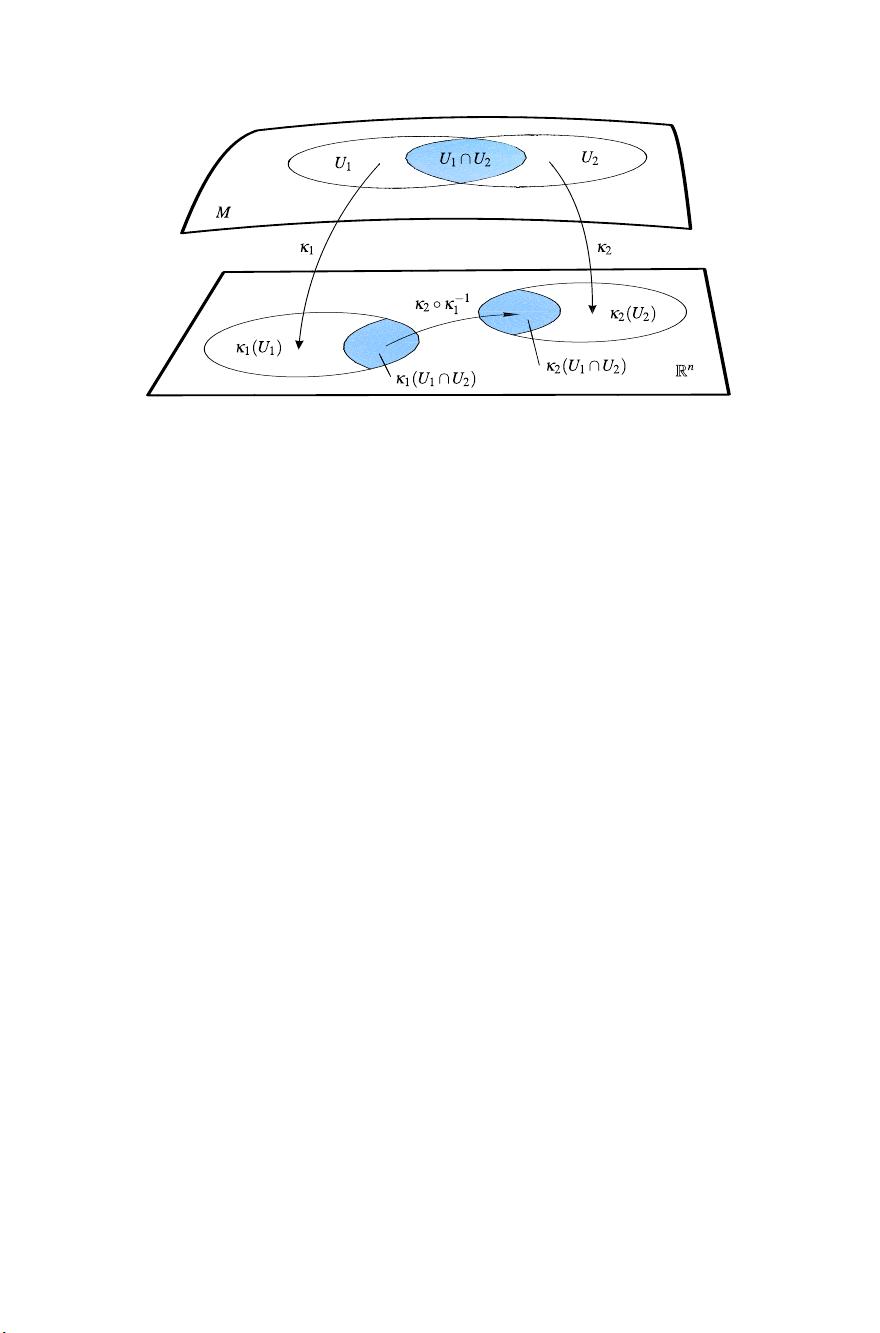
"Differential Geometry and Mathematical Physics - Part 1" 是一套旨在为物理学家和数学家提供深入学习平台的系列书籍中的第一卷，由莱比锡大学长期教授的课程内容整理而成。该书专精于基础理论，聚焦于曼氏丛论、李群以及哈密顿系统理论。作者以教学风格写作，并包含适量的基础材料，使得内容既适合研究生级别的讲座和研讨会，也便于刚进入研究领域的科学家作为深入学习的基础。在本书中，读者将探索关键概念如： 1. **曼氏丛论（Manifold）**：这是一种抽象的几何结构，它将多维空间的局部性质推广到整体上，通过光滑映射将点集与欧几里得空间联系起来，是微分几何的核心组成部分。理解曼氏丛对于研究物理中的场论和流形上的动力学至关重要。 2. **李群（Lie Group）**：这些是数学中的一个概念，它们是带有群结构的光滑流形，常用于描述物理中的对称性。李群在量子力学、粒子物理学和规范场论中扮演着核心角色，例如在规范变换和规范群（如U(1)、SU(2)和SU(3)）中的应用。 3. **哈密顿系统理论（Hamiltonian Systems）**：这是经典力学的一个分支，特别关注用哈密顿函数来描述物理系统的动力学。在量子力学中，哈密顿量是波函数演化的主要驱动力，而在这个理论框架中，李群结构对于量子化过程尤为重要。第二卷的内容则会进一步扩展到纤维丛、拓扑学以及广义相对论和规范场论的各个方面，如引力理论。这种深度和广度的结合体现了TMP系列的初衷，即为理论物理学家和数学家提供相互关联的学术资源，促进两个领域之间的交叉交流和深化理解。 "Differential Geometry and Mathematical Physics - Part 1" 是一本桥梁式教材，对于希望深入了解这些高级主题的专业人士而言，无论是作为学习工具还是研究参考，都是不可或缺的资源。

2 1 Differentiable Manifolds

Thus, we have x =



i=1

. Of course, numerically, the numbers x

and x

coin-

cide. If there is no danger of confusion, we will use the Einstein summation conven-

tion, that is, we will also write x =x

Deﬁnition 1.1.1 (Topological manifold) A topological space M is called a topo-

logical manifold if it is Hausdorff, second countable and locally homeomorphic to

for some ﬁxed n ∈ N. This means that for every m ∈ M, there exists an open

neighbourhood U of m in M and a mapping κ : U →R

such that κ(U) is open in

and κ is a homeomorphism onto its image. The pair (U, κ) is called a local chart

for M. A family A ={(U

,κ

) : α ∈ A} of local charts satisfying



α∈A

= M

is called an atlas for M. The number n is called the dimension of M.

Let (U, κ) be a local chart on M.Ifm ∈ U , we say that (U, κ) is a chart at m.

The functions

:=e

∗i

◦κ :U →R, 1 ≤ i ≤n,

deﬁne a system of local coordinates on U. The numbers κ

(m) are called the local

coordinates of m in the chart (U, κ). In particular, (R

, id

) is a global chart for

, that is, the identical mapping endows R

with the structure of a topological

manifold. The corresponding coordinates are κ

(x) =x

Remark 1.1.2

1. Since R

is not homeomorphic to R

for n =m, the dimension of a topological

manifold is unique.

2. As a consequence of being second countable, topological manifolds can have at

most countably many connected components. Moreover, every point possesses a

countable neighbourhood basis, so that one can use sequences to test topological

properties like continuity of mappings or closedness of subsets.

3. As a consequence of being locally homeomorphic to R

, topological manifolds

inherit all the local properties of R

. That is, they are locally compact (every

point has a compact neighbourhood), locally connected (every point admits a

neighbourhood basis of connected open sets), etc.

Let (U

,κ

) and (U

,κ

) be local charts on M.IfU

∩U

=∅, the mapping

◦κ

−1

⊃κ

∩U

) →κ

∩U

) ⊂R

pictured in Fig. 1.1, and its inverse κ

◦ κ

−1

are called the transition mappings

of (U

,κ

) and (U

,κ

). The transition mappings are homeomorphisms. Since

∩U

) and κ

∩U

) are open subsets of R

it makes sense to ask whether

the transition mappings are differentiable.

Deﬁnition 1.1.3 Let M be a topological manifold and let k be a nonnegative integer

or ∞.

4 1 Differentiable Manifolds

To deﬁne a differentiable structure it sufﬁces to construct an atlas. Since the union

of arbitrarily many equivalent C

-atlases is a C

-atlas, in each equivalence class

there is a unique maximal atlas. Since for any chart (U, κ) and any open subset

V ⊂ U , (V , κ

V

) is a local chart and since all these induced local charts are com-

patible of class C

with one another, all of them are contained in the maximal atlas.

Example 1.1.6 (Linear spaces) For R

itself, the single chart (R

, id

) provides

an atlas of class C

∞

. The differentiable structure deﬁned by this atlas is called the

standard smooth structure of R

and the corresponding coordinates are called the

standard coordinates on R

. Similarly, for an arbitrary open subset U ⊂ R

,the

natural inclusion mapping ι

:U →R

provides a single chart and hence deﬁnes a

smooth structure. It is clear that all of this carries over to arbitrary ﬁnite-dimensional

real vector spaces.

Example 1.1.7 (Chart domains) Let M be a manifold of class C

and let (U, κ) be a

local chart on M. Then (U, κ) is a global chart on U , thus providing a smooth atlas

on U . Hence, independently of the differentiability class of M, U together with the

atlas {(U, κ)} is a smooth manifold. It has the same dimension as M.

Example 1.1.8 (Open subsets) Let M be a manifold of class C

with atlas A and

let W ⊂M be an open subset. If (U, κ) is a local chart on M with U ∩W =∅, then

U ∩W is open in W , κ(U ∩W) is open in R

and κ

U∩W

:U ∩W →κ(U ∩W) is

a homeomorphism. Therefore,



(U ∩W,κ

U∩W

) :(U, κ) ∈A ,U ∩W =∅



is an atlas for W . Since the transition mappings of this atlas are obtained from those

of A by restriction to open subsets, they are of class C

again. Thus, the atlas A

deﬁnes a differentiable structure of class C

on W and hence W is a differentiable

manifold of the same class and the same dimension as M.

Example 1.1.9 (Spheres) The sphere S

is the set of solutions of the equation

x

= 1 in the variable x ∈ R

n+1

. In the relative topology induced from R

n+1

is Hausdorff and second countable. We construct an atlas by means of stereo-

graphic projection. Fix an arbitrary point e

∈S

, put U

:=S

\{±e

} and deﬁne

mappings κ

→R

(x) :=

x −(x ·e

1 ∓x ·e

, x ∈U

where we have identiﬁed R

with the hyperplane of R

n+1

orthogonal to e

,see

Fig. 1.2. The mappings κ

are obviously bijective, continuous and open, hence

homeomorphisms. Since U

∪ U

−

= S

, the sphere S

is a topological manifold.

The transition mapping κ

−

◦κ

−1

maps κ

∩U

−

) =R

\{0} to κ

−

∩U

−

) =

6 1 Differentiable Manifolds

Continuity of the transition mappings ensures that the (U

,κ

) are local charts

on M. Since the U

cover M and since the transition mappings are of class C

these charts establish a C

-atlas on M. The corresponding C

-structure is said to be

induced by the family of mappings {(U

,κ

)}.

Example 1.1.11 (Polar and spherical coordinates) The polar coordinates r, φ in the

plane and the spherical coordinates r, ϑ, φ in R

are curvilinear coordinates which

are often used in physical problems with rotational symmetry in order to simplify

calculations. The polar coordinate chart is deﬁned as the inverse of the mapping

×(−π,π) →R

,(r,φ)→(r cosφ,r sin φ).

Hence, the chart domain is U = R

\{λe

: λ ≤ 0}. This chart is smoothly com-

patible with the standard smooth structure on R

. By restriction to S

⊂ R

,the

coordinate function φ yields a local chart which is smoothly compatible with the

smooth structure discussed in Example 1.1.9. The spherical coordinate chart is de-

ﬁned as the inverse of the mapping

×(0,π)×(−π,π) →R

,(r,ϑ,φ)→(r sin ϑ cos φ,r sin ϑ sin φ,r cos ϑ).

Hence, the chart domain is U = R

\{λe

+ μe

: λ ≤ 0,μ ∈ R}. This chart is

smoothly compatible with the standard smooth structure on R

. By restriction to

⊂R

, the two coordinate functions φ and ϑ yield a local chart on the sphere S

which is smoothly compatible with the smooth structure discussed in Example 1.1.9.

Example 1.1.12 (Möbius strip) Let M be the topological quotient of the open subset

R ×(−1, 1) ⊂R

by the equivalence relation

) ∼(s

) iff (s

) =



+2πk,(−1)



for some k ∈Z.

M is called the Möbius strip. Let p :R×(−1, 1) →M denote the natural projection.

As the quotient of a second countable space, M is second countable. It is Hausdorff:

for m

∈M, deﬁne

d(m

) =inf





−s

)

+(t

−t

)

:(s

) ∈p

−1

), i =1, 2



(1.1.1)

and show that d isametriconM, compatible with the quotient topology (Exer-

cise 1.1.3). To construct an atlas, we show that p is open. For every k ∈ Z,the

mapping

:R ×(−1, 1) →R ×(−1, 1), ϕ

(s, t) :=



s +2πk,(−1)



is a homeomorphism. If O ⊂R ×(−1, 1) is open, then ϕ

(O) and hence

−1



p(O)





k∈Z

(O)

剩余772页未读，继续阅读

xavierjuan

粉丝: 0
资源: 7

黎曼几何与数学物理入门：曲面、Lie群与哈密顿系统

Notes on Differential Geometry and Lie Groups - A Second Course.pdf

Differential Geometry Curves - Surfaces - Manifolds

3D image retrieval based on differential geometry and co-occurrence matrix

Differential Geometry in Physics

ordinary-and-partial-differential-equation-routines-in-c-c-fortran-java-maple-and-matlab

Ordinary Differential Equations and Dynamical Systems - G. Teschl

Ordinary differential equations and dynamical systems-G. Teschl

Differential-and-Integral-Methods:微分和积分方法，理学士特拉维夫大学电气和电子工程

Numerical-Differential-Evolution-Algorithm-and-Benchmark-Functions:人工智能最终项目介绍

Differential Equations and Linear Angebra -Scott A. Annin.pdf

最新资源