非线性方程求根方法探讨：牛顿法与割线法应用

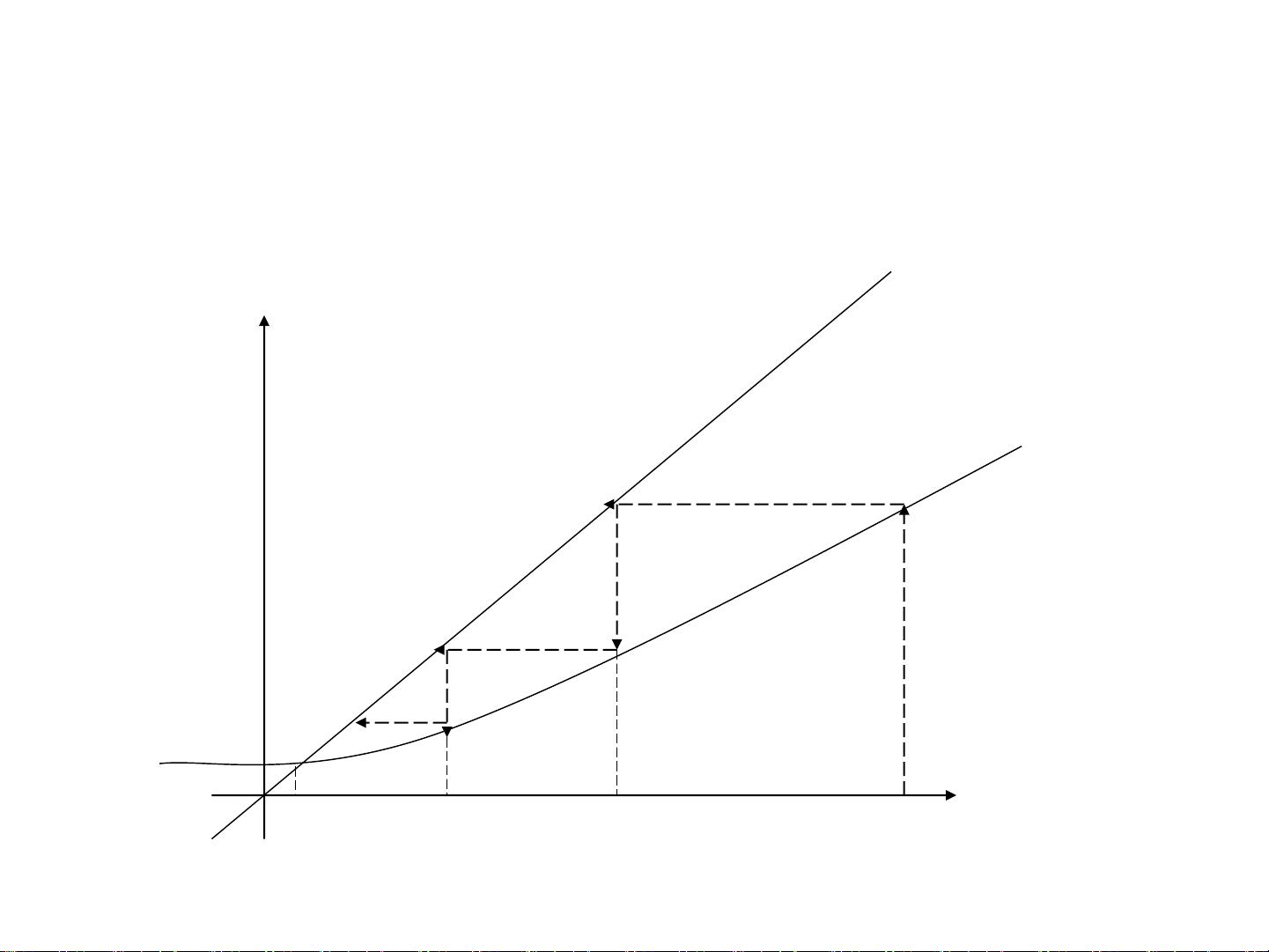
数值分析中的非线性方程求根是计算机科学和工程领域中的关键课题，它涉及在没有解析解的情况下寻找函数f(x) = 0的近似解。非线性方程与线性方程组不同，其解并非简单的线性组合，而是函数值在某点达到零点的情况。本章内容分为以下几个部分： 1. 基本概念：非线性方程的定义明确指出，若函数f(x)在闭区间[a, b]上连续且满足f(a)f(b) < 0，根据介值定理，至少存在一个根x*使得f(x*) = 0。根的类型包括单根（m=1）和重根（m>1），以及代数多项式的特殊性质，如n次代数方程在复数域内的根的总数。 2. 牛顿法：作为常用的数值求根方法，牛顿法基于迭代过程，通过构造函数的切线来逼近零点。该方法利用函数f(x)和其导数f'(x)的值，不断更新猜测解，直到满足预定精度。 3. 割线法：另一种求解策略是割线法，它通过连接两个相邻迭代点，形成一条割线，并找到割线与x轴的交点，作为新的猜测解。这种方法通常用于牛顿法的改进或替代方案，特别是在函数不可导或者导数计算困难时。 4. 非线性方程组求根：非线性方程组不仅涉及到单个方程，还可能涉及到多个方程的联立求解。这类问题通常更复杂，需要更高级的数值方法，如迭代算法（如高斯-赛德尔法、雅可比迭代法等）。 5. 具体例子：章节中提供了代数方程（如x^5 - x^3 + 24x + 1 = 0）和超越方程（如sin(5x^2) + e^(-x) = 0）的例子，强调了非线性方程求根在实际问题中的应用，以及当高次方程或超越方程缺乏解析解时的重要性。 6. 二分法：作为基础的数值求根方法，二分法通过不断将区间缩小，逐步逼近根的位置，虽然简单直观，但并不总是最有效率的。对于某些情况，可能需要采用更复杂的算法以提高搜索效率和精度。 数值分析中的非线性方程求根技术是科学计算和工程问题的核心组成部分，掌握这些方法对于解决实际问题具有重要意义。后续章节将详细介绍各种求根算法的原理、收敛性以及适用场景，为理解和实施这些算法提供全面的指导。