高斯核函数在人口普查数据预测中的应用

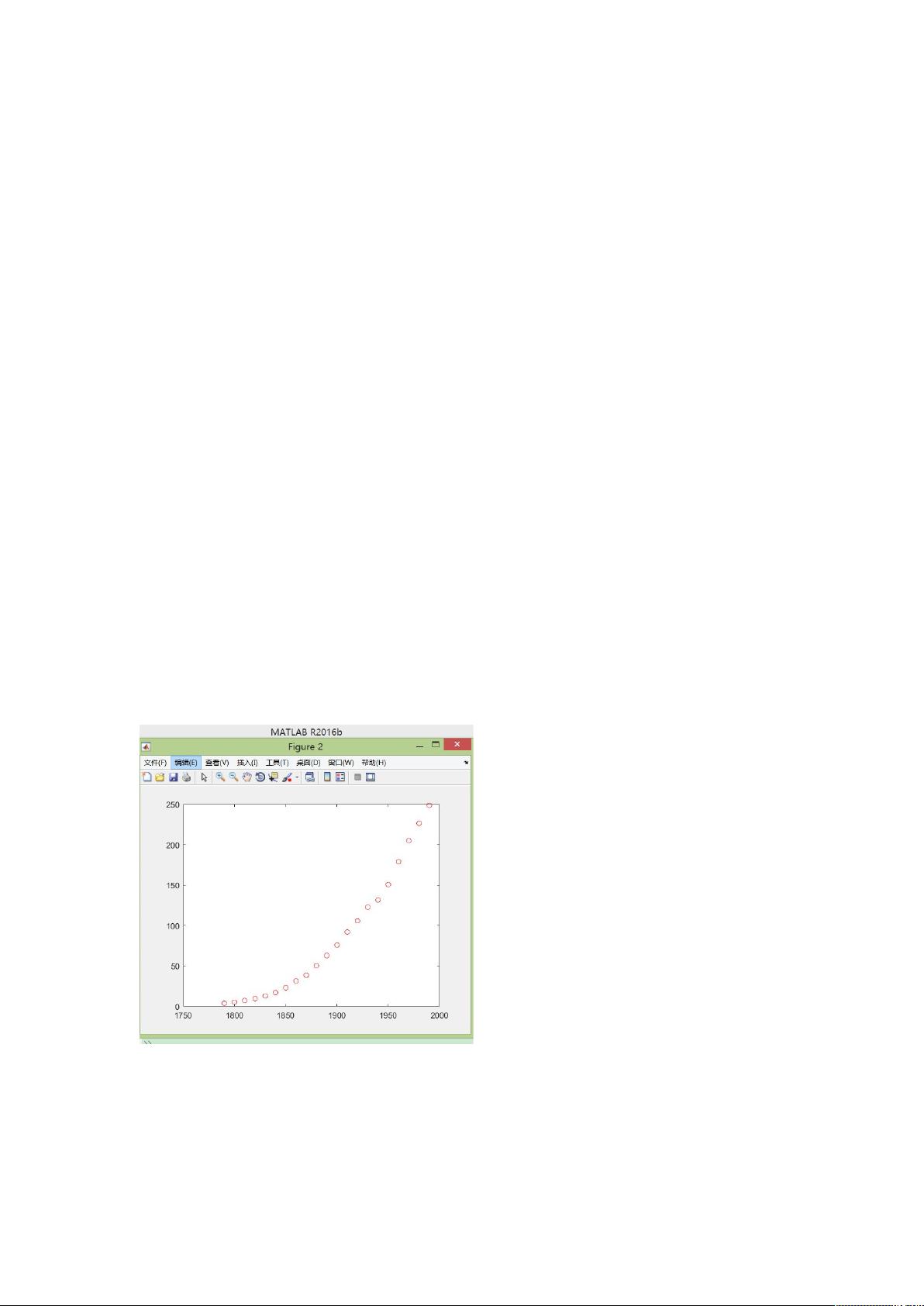
"正则方程与核算法在人口普查数据中的应用——以美国人口预测为例" 这篇描述涉及的是利用正则方程和核算法来处理人口普查数据，特别是线性回归模型和高斯核（Gaussian kernel）在预测美国人口中的应用。首先，我们从加载的数据集中获取了日期（cdate）和人口（pop）两个变量，并用红色圆点在图上标出了这两个变量的关系。 在统计学和机器学习中，线性回归是一种常见的模型，用于预测连续数值型的响应变量。在这个例子中，我们使用了最小二乘法（通过矩阵运算pseudoinverse）来求解线性回归的权重向量`hw`。线性回归模型假设因变量（人口）与自变量（时间）之间存在线性关系，但现实情况往往并非如此简单，因此引入核算法来处理非线性问题。 高斯核，也称为径向基函数（Radial Basis Function，RBF），是一种常用的核函数，它可以将数据映射到高维空间，使得在高维空间中的数据更容易线性可分。函数`KGaussian`用于计算两个样本之间的高斯核。它接受输入参数`A`（完整数据集）、`tilde_A`（可以是完整数据集或其子集）以及`sigma`（高斯核的带宽参数），并返回一个核矩阵`K`。高斯核的公式为`K(i,j) = exp(-gamma * ||A_i - tilde_A_j||_2^2)`，其中`gamma`是控制核函数宽度的参数，`||.||_2`表示欧氏距离。 在实际操作中，我们首先对数据进行预处理，将日期`x`和人口`y`绘制成散点图，然后使用线性回归模型预测的人口值`yhat`与实际值`y`进行比较，计算决定系数（R-squared，即`R2`），这能衡量模型拟合优度。较大的`R2`值表示模型对数据的解释能力越强。接着，我们使用同样的模型在新的日期范围`xfit`上进行预测，并绘制出蓝色直线`yfit`，以便于视觉对比。 最后，代码暂停以展示结果，这允许用户观察和分析图形。整个过程展示了如何利用核方法，特别是高斯核，来处理非线性的关系，例如在人口预测中的复杂趋势。 总结来说，这个例子深入探讨了如何结合正则方程和高斯核算法来处理非线性关系，特别是在人口普查数据的线性建模中。通过使用核方法，我们可以有效地将数据转换到一个更复杂的特征空间，从而在原始数据可能无法找到的模式中找到关联。