DOA估计：古典与现代方法探索

5星 · 超过95%的资源需积分: 9 91 浏览量更新于2024-07-31 收藏 4.37MB PDF 举报

"Classical and Modern DOA Estimation" 本书《Classical and Modern DOA Estimation》是2009年由Elsevier出版的一部专注于方向-of-arrival (DOA)估计技术的专业文献，它集合了在Elsevier数据上发表的相关论文，为读者提供了丰富的DOA估计算法和理论知识。DOA估计是信号处理领域的一个关键问题，特别是在无线通信、雷达系统和声学传感器网络中，用于确定信号源相对于接收阵列的方向。 DOA估计算法主要包括经典方法和现代方法。经典方法通常涉及数学统计和矩阵理论，如最大似然（ML）估计、最小二乘（LS）估计和音乐算法（MUSIC）。这些方法基于阵列信号处理，利用多通道接收信号之间的相位差来确定信号源的方向。例如，最大似然估计通过寻找最可能产生观测数据的信号源方向来估计DOA，而音乐算法则利用特征值分解来识别噪声子空间，从而估计信号源的方向。现代DOA估计技术则涵盖了更广泛的领域，包括阵列信号处理的高级理论、机器学习和人工智能算法。例如，基于稀疏表示的DOA估计利用信号的稀疏特性来提高估计精度，这在噪声环境复杂的情况下特别有效。此外，现代方法还包括利用神经网络和深度学习的方法，通过训练模型来直接预测DOA，这种方法可以自动学习信号特性和阵列配置的复杂关系，进一步提升DOA估计的性能。书中可能还探讨了阵列几何结构的影响，如线性阵列、圆阵列和随机分布阵列等，以及各种阵列处理技术，如波束形成、自适应滤波和空间谱估计。每种阵列结构都有其特定的优势和适用场景，如线性阵列适用于平面波入射，而圆阵列可以提供全方位的覆盖。除了理论分析外，本书可能还包含实际应用案例和实验结果，以展示不同DOA估计方法在真实世界情境中的表现。这有助于读者理解如何选择合适的DOA估计技术，并将其应用于实际系统设计中。此外，版权信息提醒读者，本书内容受到严格保护，未经许可不得复制或传播。如果需要使用其中的内容，应事先获得出版社的授权。读者可以通过Elsevier的官方网站获取权限申请相关信息。《Classical and Modern DOA Estimation》是了解和深入研究DOA估计技术的重要参考资料，无论对于学术研究者还是工程实践者，都能从中获益良多。

Section | 1.2 Problem Formulation

where x

(t) is the vector of the received passband signals and τ

are the

propagation delays determined by the direction of the source relative to the

array. For example, in the case of a linear array

=τ

−(d

/c) sin θ (1.2)

where τ

is the propagation delay from the emitter to a reference point on the

array, d

are the distances of the array elements from that reference point, c is

the speed of light, and θ is the emitter direction measured relative to the line

perpendicular to the array. Without loss of generality we can assume that τ

=0.

(This is equivalent to deﬁning s(t) as the baseband signal at the reference point

of the receiver array, not as the source signal.) Thus, in the rest of this chapter

we will assume that

=−(d

/c) sin θ (1.3)

We note that the contribution of τ

to the phase e

−jw

introduces an unknown

random phase term that is common to the elements of the received signal vector.

Because of this phase term, all direction-ﬁnding methods must be designed to

be invariant to a common additive phase.

After transforming the passband signals to baseband, we have

x(t) =

⎡

⎢

⎣

s(t −τ

⎤

⎥

⎦

(1.4)

where x(t) is the vector of received baseband signals.

Let D denote the aperture of the array in wavelengths λ. Then Dλ/c =D/f

is the time it takes the signal to propagate over the array, so that τ

< D/f

.It

follows that, if the signal bandwidth is B and B f

/D, s(t −τ

) ≈s(t). The

condition B  f

/D or B/f

1/D implies that s(t) is a narrowband signal. It

follows that, under the narrowband assumption, the received baseband signal

can be written as

x(t) =s(t)

⎡

⎢

⎣

⎤

⎥

⎦

(1.5)

For this reason, we deﬁne the so-called “array manifold” a(θ), as the array

response to a unit amplitude signal (i.e., the case where s(t) =1).

a(θ) =

⎡

⎢

⎣

exp{ j2πd

sin θ/λ}

exp{ j2πd

sin θ/λ}

exp{ j2πd

sin θ/λ}

⎤

⎥

⎦

(1.6)

Chapter | 1 Wireless Direction-Finding Fundamentals

With no loss of generality we assume that the signal s(t) has unit power, in which

case the complete narrowband model for the received signal can be written as

y(t) =

√

SNRs(t)a(θ

) +v(t) (1.7)

where v(t) is a multivariate complex Gaussian noise vector with uncorrelated

elements having zero mean and unit variance, θ

is the direction of the emitter,

and SNR is the signal-to-noise ratio.

Direction-ﬁnding methods often use sampled versions of the array output, in

which case

y[k]=

√

SNRs[k]a(θ

) +v[k] (1.8)

where k is the index of the sample, or the “snapshot.” The noise v[k] is assumed

to be independent from snapshot to snapshot. The signal s[k] may or may not be

independent from snapshot to snapshot, depending on its temporal correlation

properties. Equation (1.8) deﬁnes the narrowband signal model used in the rest

of this chapter.

1.3 DIRECTION-FINDING ALGORITHMS

We now describe three common methods for direction ﬁnding using an antenna

array. The ﬁrst two involve linear combinations of the received signals; the third

is nonlinear.

1.3.1 Beamforming

Combining the antenna outputs so that the signals from a given direction “line

up,” and can thus be added coherently, is the fundamental method used in array-

processing applications. Recall that the passband signal received by the array’s

mth element is x

(t) =s(t −τ

(θ

))e

(t−τ

(θ

)

, where the delays are functions

of the emitter direction θ

and the array geometry.

With proper delays applied to them, the received signals line up. Assume that

(t) is delayed by τ −τ

(θ

) to yield x

(t −τ −τ

(θ

)) =s(t −τ)e

(t−τ)

.In

other words, the properly delayed array outputs are identical and can be added up

to enhance the signal-to-noise ratio at the receiver by a factor of M, the coherent

array gain.

If a different set of delays is used corresponding to θ =θ

, the signals will

not line up and the result of the sum will be a signal with power that is smaller

than in the case where θ =θ

. Thus, the signal power at the beamformer output

will be maximized in the correct direction.

The processing just described, called delay-and-sum beamforming, can be

used for both wideband and narrowband signals. In the case where a signal is

narrowband, the beamformer can be implemented using appropriate phase shifts

instead of time delays. As was shown in Equation (1.5) the received signal

Section | 1.3 Direction-Finding Algorithms

vector is represented (up to a common factor) by the array manifold a(θ).

Combining the signals “in phase” is accomplished by the complex conjugate

of the array manifold. Thus, we compute |a(θ)

a(θ

)|. If the assumed direction

θ equals the true emitter direction, we get the largest value of the combined

signals |a(θ

)

a(θ

)|=M.Ifθ =θ

, the signals are not added in phase and the

result of the sum is smaller. This type of processing is called frequency domain

beamforming or just beamforming.

In its most general form, a beamformer uses a weight vector W(θ) to lin-

early combine the array outputs. In most applications we are interested in the

magnitude or the power of the combiner output. In the latter case the output is

given by

p(θ) =|W(θ)

(1.9)

where y is the received signal. In the absence of noise and assuming a unit power

signal, the beamformer output is

p(θ) =SNR|W(θ)

a(θ

(1.10)

When the beamformer is used for direction ﬁnding, its output p(θ) is computed

over a range of directions θ. The direction where p(θ) reaches its largest value

is the estimated emitter direction.

In this discussion we assume that W(θ) =a(θ). In practice, this weight vector

will be modiﬁed by a window chosen to suppress the sidelobe level of the beam

pattern to a desired level. We use a normalized but nonwindowed weight vector

W(θ) =a(θ)/|a(θ)|, which makes the noise power at the beamformer output the

same as at the antenna elements.

It should be noted that the beamformer with this choice of weight vector is

in fact the generalized maximum likelihood estimator of the direction θ, for the

signal model

y =α

a(θ

) +v (1.11)

where y is the vector of the signals at the array output, α

is a complex scale

factor assumed to be unknown (α

√

SNR s in the previous notation), a(θ) is

the array manifold, θ

is the unknown emitter direction, and v is a noise vector

composed of independent zero-mean unit-variance Gaussian random variables.

The generalized maximum likelihood estimate is given by joint minimization

of the error |y−α

a(θ

over the unknowns θ

and α

. Minimizing ﬁrst over

we have α

(θ

)y/a

(θ

)a(θ

). Inserting this into the error function we

have |y −a(θ

(θ

)/|a(θ

. Minimizing this cost function with respect to

is equivalent to maximizing y

a(θ

(θ

)y/|a(θ

, which can be written

as |W

(θ

)y|

, the output of the beamformer presented earlier. Thus, the estimate

obtained by maximizing the output power of the beamformer is the generalized

likelihood direction estimate.

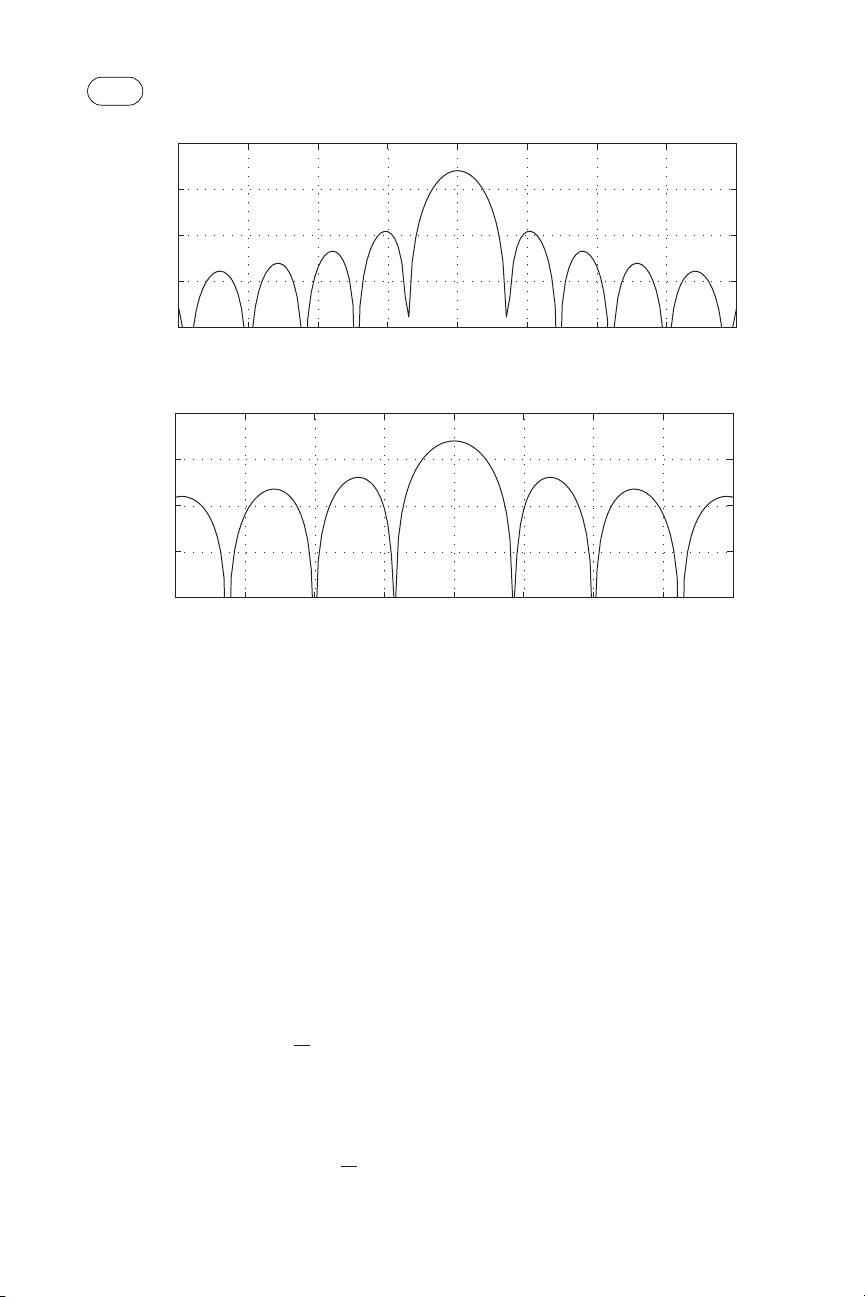
Figure 1.2 depicts the beam pattern p(θ) for 16-element circular and linear

arrays in the case where θ

=0. As can be seen, p(θ) is maximized at the source

剩余435页未读，继续阅读

jinsanshao

粉丝: 0
资源: 2

DOA估计：古典与现代方法探索

[2009] Channel Codes Classical and Modern

Classical and Modern Optics

A Simplified approach to image processing in C: Classical and Modern Techniques in C

classical and modern direction-of-arrival estimation

channel codes: classical and modern

from modelscope import snapshot_download model_dir = snapshot_download('jeruen/classical_zh_modern_zh') 我想使用这个模型应该怎么编程

Describe the classical pipeline of data processing, especially the intentions of each phase of the pipeline

如何获取Classical Chinese Poetry Dataset

最新资源