Dijkstra算法解决最短路径问题

"该资源是一份关于图论与回归问题的课件，主要讲解了Dijkstra算法在寻找图中两点间最短路径的应用，并通过实例和代码解释了算法的实现过程。" 这篇课件深入浅出地介绍了图论中的Dijkstra算法。Dijkstra算法是一种用于解决单源最短路径问题的有效算法，它适用于有权图（即图中的边带有权重）。在无环且权重非负的情况下，Dijkstra算法能够找到从起点到图中其他所有顶点的最短路径。 首先，课件区分了三种类型的图：无向图、有向图和混合图。无向图的边没有方向，而有向图的边有明确的方向。混合图则是包含有向边和无向边的图。在这些图中，Dijkstra算法通常用于有向图，但也可以应用于无向图，因为无向图可以看作是有向图的特殊情况。 课件以一个具体的例子展示了Dijkstra算法的步骤。这个例子是从顶点①出发寻找到达顶点⑨的最短路径。算法步骤包括： 1. 初始化：将起点①标记为已访问（P），其他顶点标记为未访问（T），并计算从起点出发的最短路径。 2. 扩展：遍历已访问的顶点，寻找可以到达未访问顶点的最短边，并更新未访问顶点的最短路径。 3. 重复以上步骤，直到所有顶点都被访问或目标顶点被标记为已访问。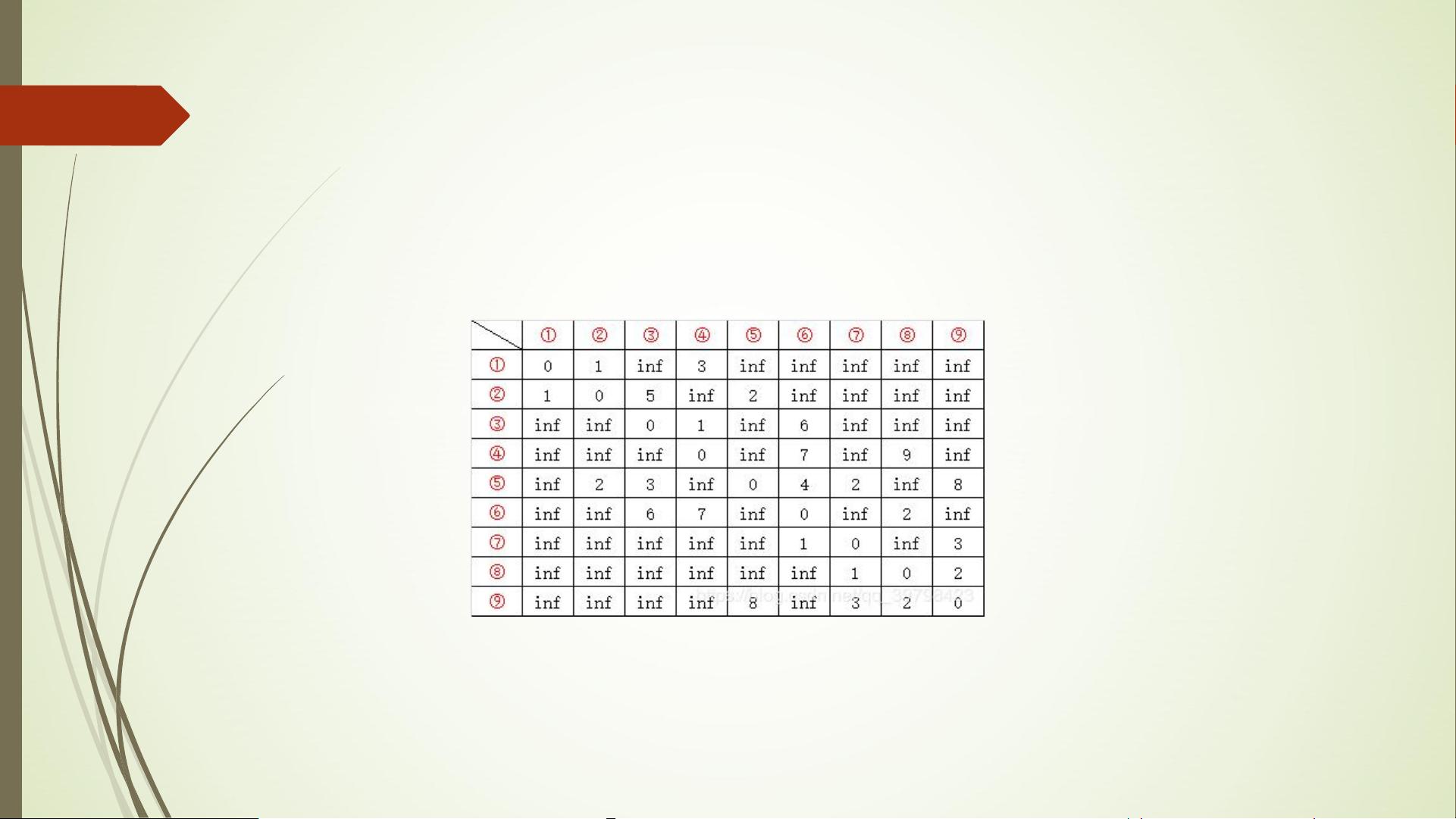 在实例中，课件详细列出了每个步骤的顶点状态变化，直到找到最短路径。同时，课件还介绍了带权邻接矩阵的概念，这是一个二维数组，用于表示图中顶点之间的距离。矩阵的对角线元素表示顶点到自身的距离（通常是0），非对角线元素表示两个顶点间的距离。如果两个顶点间无边相连，则距离记为无穷大（通常用一个较大的常数表示）。 最后，课件给出了Dijkstra算法的Python实现，使用了`defaultdict`和`heapq`库。代码中定义了不连通值`inf`，并展示了如何根据带权邻接矩阵进行迭代，逐步更新最短路径。 这份课件是学习Dijkstra算法及其应用的一个很好的资源，对于理解图论中的最短路径问题以及如何在实际编程中实现这一算法具有很大的帮助。