深度生成模型：构建能想象与推理的机器

需积分: 10 92 浏览量更新于2024-07-20 收藏 12.49MB PDF 举报

Shakir Mohamed是一位在机器学习领域有着深厚影响力的专家，他在2016年的Deep Learning Summer School上分享了主题为“Building Machines that Imagine and Reason”的演讲。该演讲探讨了深度生成模型（Deep Generative Models）的基本原则及其广泛应用。深度生成模型是一种解决无监督学习问题的关键工具，这种类型的机器学习系统能够在没有标签数据的情况下揭示隐藏的结构。由于它们具备生成能力，这些模型能够构建一个丰富的内在世界想象，这使得机器能够探索数据变化、理解世界的结构和行为，并最终支持决策制定。在这次演讲中，Shakir强调了如何利用深度生成模型来构建能够想象的机器学习系统。他解释了这些模型是如何通过概率推断实现的，例如通过生成对抗网络（GANs）、变分自编码器（VAEs）或自注意力机制等技术，使机器能够从随机噪声中生成逼真的样本。深度生成模型在多个实际场景中发挥着重要作用，如密度估计、图像去噪和生成式对抗网络的艺术创作等。深度生成模型的另一个关键应用是用于生成式对话系统，通过模拟人类对话的模式来提供更自然、连贯的交流。此外，它们还可以用于推荐系统，通过分析用户的行为模式预测潜在的兴趣，并据此做出个性化推荐。在强化学习中，生成模型也用于模拟环境，帮助智能体在复杂环境中进行策略规划和决策。 Shakir还讨论了深度生成模型在科学发现、自然语言处理和计算机视觉中的潜在作用，特别是在理解和生成复杂的数据分布方面。他可能提到了如何利用这些模型进行序列建模，例如文本生成或者音乐创作，以及如何通过生成模型来提升模型的泛化能力和适应性。 Shakir Mohamed的演讲不仅深入剖析了深度生成模型的核心原理，还展示了其在实际问题解决中的广泛实用性。听众不仅可以了解到如何构建具备想象力的机器，还能掌握如何将这些模型融入到各种应用场景中，以推动人工智能的发展并解决现实世界中的挑战。

Machines that Imagine and Reason

(a) (b) (c)

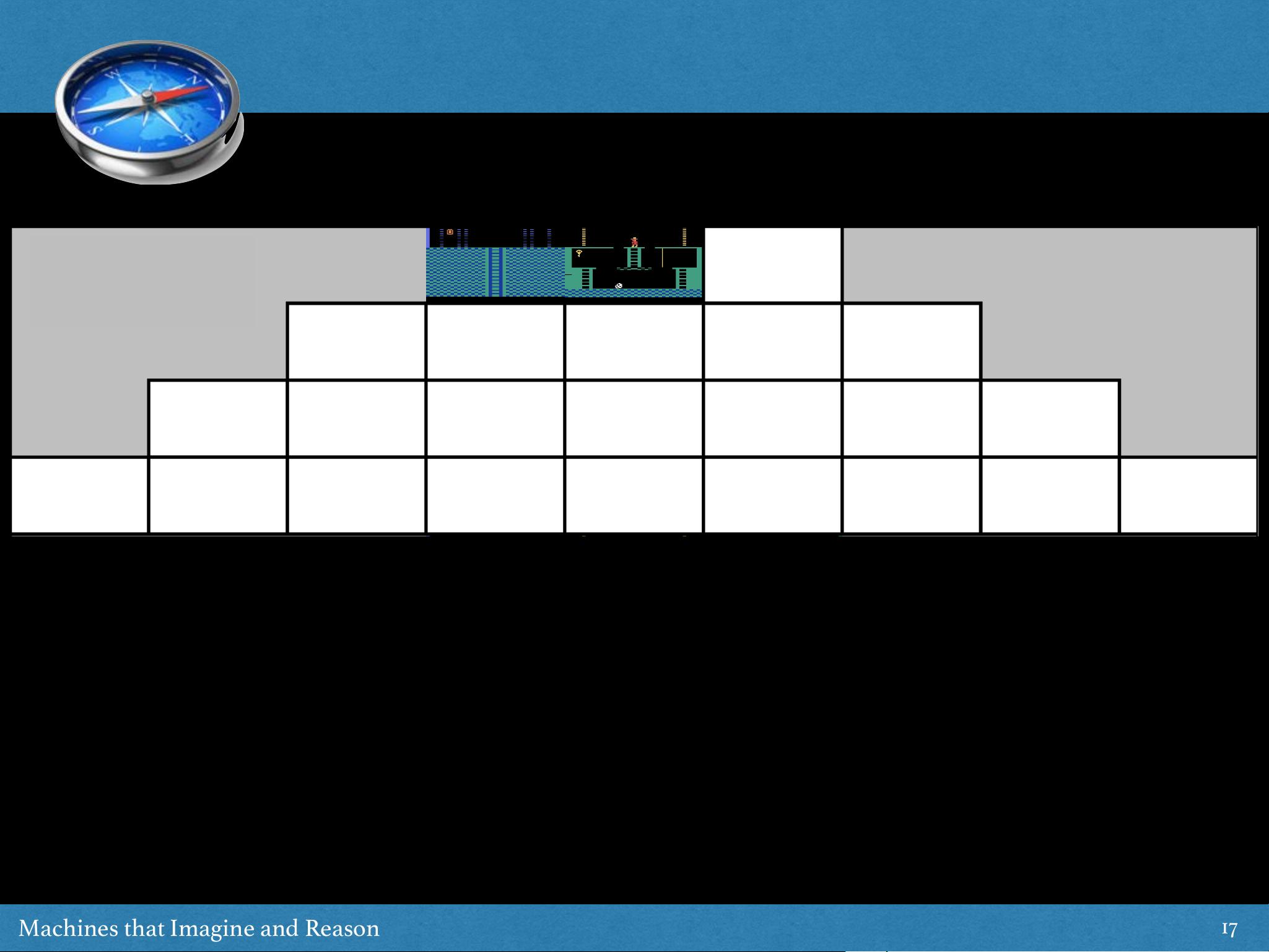
Figure 2: High-resolution screenshots of the Labyrinth environments.

(a)

Forage and Avoid showing

the apples (positive rewards) and lemons (negative rewards).

(b)

Double T-maze showing cues at

the turning points.

(c)

Top view of a Double T-maze conﬁguration. The cues indicate the reward is

located at the top left.

state was discarded. The

-nearest-neighbour lookups used

k = 50

. The discount rate was set to

 =0.99

. Exploration is achieved by using an

✏

-greedy policy with

✏ =0.005

. As a baseline, we

used A3C [

]. Labyrinth levels have deterministic transitions and rewards, but the initial location

and facing direction are randomised, and the environment is much richer, being 3-dimensional. For

this reason, unlike Atari, experiments on Labyrinth encounter very few exact matches in the buffers

of Q

-values; less than 0.1% in all three levels.

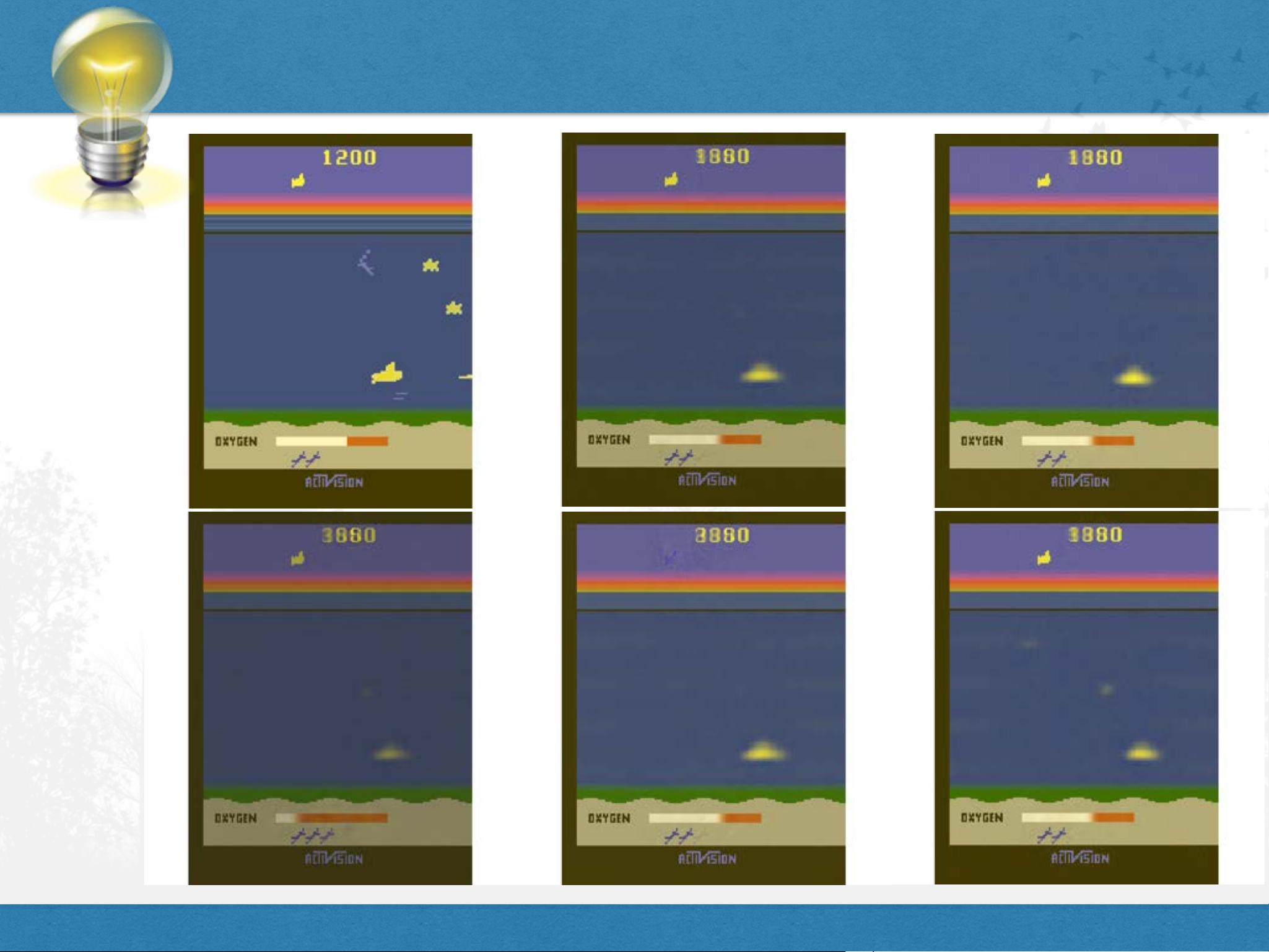
Each level is progressively more difﬁcult. The ﬁrst level, called Forage, requires the agent to collect

apples as quickly as possible by walking through them. Each apple provides a reward of 1. A simple

policy of turning until an apple is seen and then moving towards it sufﬁces here. Figure 1 shows that

the episodic controller found an apple seeking policy very quickly. Eventually A3C caught up, and

ﬁnal outperforms the episodic controller with a more efﬁcient strategy for picking up apples.

The second level, called Forage and Avoid involves collecting apples, which provide a reward of 1,

while avoiding lemons which incur a reward of

1

. The level is depicted in Figure 2(a). This level

requires only a slightly more complicated policy then Forage (same policy plus avoid lemons) yet

A3C took over 40 million steps to the same performance that episodic control attained in fewer than

3 million frames.

The third level, called Double-T-Maze, requires the agent to walk in a maze with four ends (a map

is shown in Figure 2(c)) one of the ends contains an apple, while the other three contain lemons.

At each intersection the agent is presented with a colour cue that indicates the direction in which

the apple is located (see Figure 2(b)): left, if red, or right, if green. If the agent walks through a

lemon it incurs a reward of

1

. However, if it walks through the apple, it receives a reward of

, is

teleported back to the starting position and the location of the apple is resampled. The duration of an

episode is limited to 1 minute in which it can reach the apple multiple times if it solves the task fast

enough. Double-T-Maze is a difﬁcult RL problem: rewards are sparse. In fact, A3C never achieved

an expected reward above zero. Due to the sparse reward nature of the Double T-Maze level, A3C did

not update the policy strongly enough in the few instances in which a reward is encountered through

random diffusion in the state space. In contrast, the episodic controller exhibited behaviour akin to

one-shot learning on these instances, and was able to learn from the very few episodes that contain

any rewards different from zero. This allowed the episodic controller to observe between 20 and 30

million frames to learn a policy with positive expected reward, while the parametric policies never

learnt a policy with expected reward higher than zero. In this case, episodic control thrived in sparse

reward environment as it rapidly latched onto an effective strategy.

4.3 Effect of number of nearest neighbours on ﬁnal score

Finally, we compared the effect of varying

(the number of nearest neighbours) on both Labyrinth

and Atari tasks using VAE features. In our experiments above, we noticed that on Atari re-visiting

the same state was common, and that random projections typically performed the same or better

than VAE features. One further interesting feature is that the learnt VAEs on Atari games do not

yield a higher score as the number of neighbours increases, except on one game, Q*bert, where

VAEs perform reasonably well (see Figure 3a). On Labyrinth levels, we observed that the VAEs

outperformed random projections and the agent rarely encountered the same state more than once.

Interestingly for this case, Figure 3b shows that increasing the number of nearest neighbours has a

Representation Learning for Control

Machines that Imagine and Reason

Density-based Exploration

No bonus

With bonus

Figure 4: “Known world” of a DQN agent trained for 50 million frames with (bottom) and without

(top) count-based exploration bonuses, in M

ONTEZUMA’S REVENGE.

7.3 Improving exploration for actor-critic methods.

We next turn our attention to actor-critic methods, speciﬁcally the A3C (asynchronous actor-critic)

algorithm of Mnih et al. (2016). One appeal of actor-critic methods is that their explicit separation

of policy and Q-function parameters allows for a richer behaviour space. This very separation, how-

ever, often leads to deﬁcient exploration: to produce any sensible results, the A3C policy parameters

must be regularized with an entropy cost (Mnih et al., 2016). As we now show, our count-based

exploration bonus leads to signiﬁcantly improved A3C performance.

We ﬁrst trained A3C on 60 Atari 2600 games, with and without the exploration bonus given by (6).

We refer to our augmented algorithm as A3C+. From a parameter sweep over 5 training games we

found the parameter  =0.01 to work best. Summarily, we ﬁnd that A3C fails to learn in 15 games,

in the sense that the agent does not achieve a score 50% better than random. In comparison, there

are only 10 games for which A3C+ fails to improve on the random agent; of these, 8 are games

where DQN fails in the same sense. Details and full results are given in the appendix.

To demonstrate the beneﬁts of augmenting A3C with our exploration bonus, we computed a baseline

score (Bellemare et al., 2013) for A3C+ over time. If r

is the random score on game g, a

the

performance of A3C on g after 200 million frames, and s

g,t

the performance of A3C+ at time t,

then the corresponding baseline score at time t is

g,t

 min{r

}

max{r

}  min{r

}

Figure 5 shows the median and ﬁrst and third quartile of these scores across games. Considering the

top quartile, we ﬁnd that A3C+ reaches A3C’s ﬁnal performance on at least 15 games within 100

million frames, and in fact reaches much higher performance levels by the end of training.

7.4 Comparing exploration bonuses.

Next we compare the effect of using different exploration bonuses derived from our density model.

We consider the following variants:

• no exploration bonus,

•

(x)

1/2

, as per MBIE-EB (Strehl and Littman, 2008);

•

(x)

1

, as per BEB (Kolter and Ng, 2009); and

• PG

(x), related to compression progress (Schmidhuber, 2008).

The exact form of these bonuses is analogous to (6). We compare these variants after 10, 50, 100,

and 200 million frames of training, using the same experimental setup as in the previous section. To

剩余88页未读，继续阅读

蓝魅派

粉丝: 0
资源: 10

深度生成模型：构建能想象与推理的机器

论文研究 - Badr Shakir Al-Sayyab在《 Sifr Ayoub》中的救赎与审美结构

Generative Models

Shakir_185_C_Repository

2016_NIPS_VI_tutorial

Advances in Machine Learning and Signal Processing

博客首页模板 .sketch素材下载

TechnicalReference-Cdd-Communication.pdf

古兰经比较和搜索 - 需要 Matlab：比较古兰经的 10 个翻译与搜索-matlab开发

Teddy Bear v1.2.unitypackage

C#ASP.NET体育馆综合会员管理系统源码数据库 SQL2008源码类型 WebForm

最新资源