Python KMeans算法详解：从概念到实践

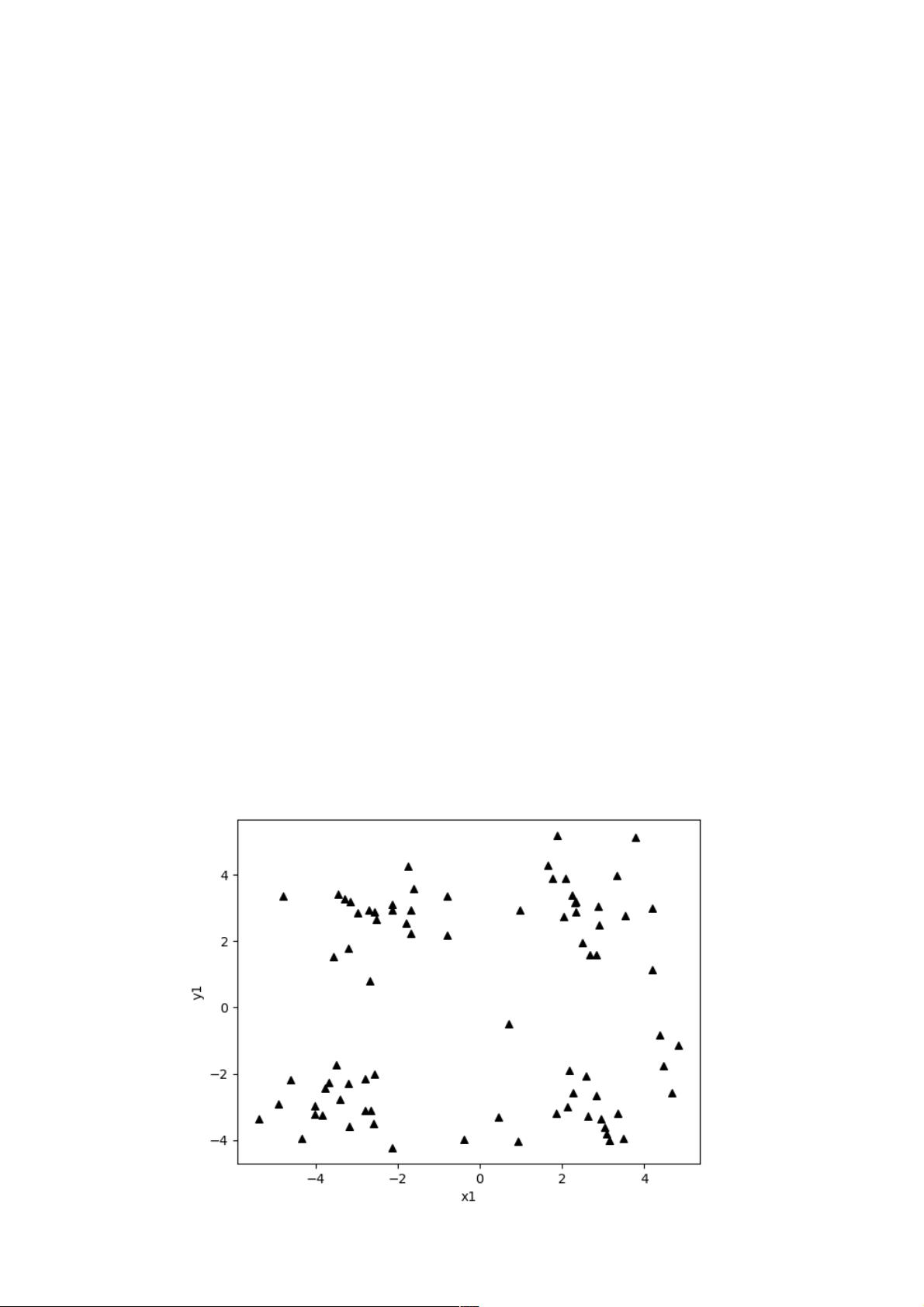
"深入解析Python KMeans算法，包括无监督学习概念、聚类目的及KMeans算法的基本原理。本文提供了一组二维数据点作为示例，解释了如何通过欧式距离找到簇中心。" KMeans算法是一种广泛应用的无监督学习方法，主要用于数据的聚类。在无监督学习中，我们没有预先定义的类别标签，目标是从数据的内在结构中学习模式。聚类是无监督学习的一种，它的任务是将相似的数据分到同一组，即“簇”。 KMeans算法的核心思想是迭代寻找簇的中心（质心），并将数据点分配给最近的质心所在的簇。以下是对KMeans算法步骤的详细解释： 1. 初始化：选择K个初始质心。这通常可以通过随机选择K个数据点来实现。在本例中，我们假设K=4。 2. 分配阶段：计算每个数据点与所有质心的距离，使用的是欧式距离。欧式距离是两点之间的直线距离，公式为：`d = sqrt(sum((x_i - y_i)^2))`，其中x和y是两个点的坐标，i是坐标轴索引。 3. 更新质心：一旦所有数据点被分配到对应的簇，就更新每个簇的质心。质心是该簇内所有数据点坐标平均值的位置，即簇内所有点的均值向量。 4. 迭代：重复分配和更新质心的过程，直到质心不再显著移动（达到收敛条件），或者达到预设的最大迭代次数。 在实际应用中，选择合适的K值是关键，可以使用肘部法则或者轮廓系数等方法来确定最佳的簇数。肘部法则通过观察随着K增加，簇内的平方误差总和的变化趋势，选择“肘部”处的K值，即增加簇的数量带来的改善效果开始显著减小的点。 对于给定的二维数据点，KMeans算法会迭代地更新质心，最终形成4个簇。在每个迭代过程中，数据点将根据与当前质心的距离重新分配，直到质心稳定，即每个簇内的点相对固定，且簇间距离最大化。 需要注意的是，KMeans算法有一些局限性，如对初始质心敏感可能导致不同的结果，对异常值敏感，以及对非凸形状的簇识别能力有限。此外，KMeans假设簇是球形的，并且大小一致，对于复杂的数据分布可能不适用。因此，在实际应用中，可能需要结合其他聚类算法或者预处理步骤来优化结果。