傅里叶变换应用手册：matlab和C语言程序.pdf

傅里叶变换在信号处理领域中具有广泛的应用。通过对信号进行傅里叶变换，可以将信号从时域转换到频域，从而更好地理解信号的频率成分和特征。在实际应用中，人们常常使用傅里叶变换来分析和处理各种类型的信号，如音频信号、图像信号等。 为了方便进行傅里叶变换的计算，人们编写了各种程序来实现这一过程。其中，Matlab程序和C语言程序是两种常见的计算工具，它们能够根据给定的信号进行快速傅里叶变换（FFT）计算。通过这些程序，用户可以方便地获取信号在频域上的表示，进而进行进一步的分析和处理。 在实际的信号处理任务中，常常需要对连续时间信号进行傅里叶变换。对于一个连续时间信号$x(t)$，我们可以通过积分来求取其傅里叶变换$X(\omega)$。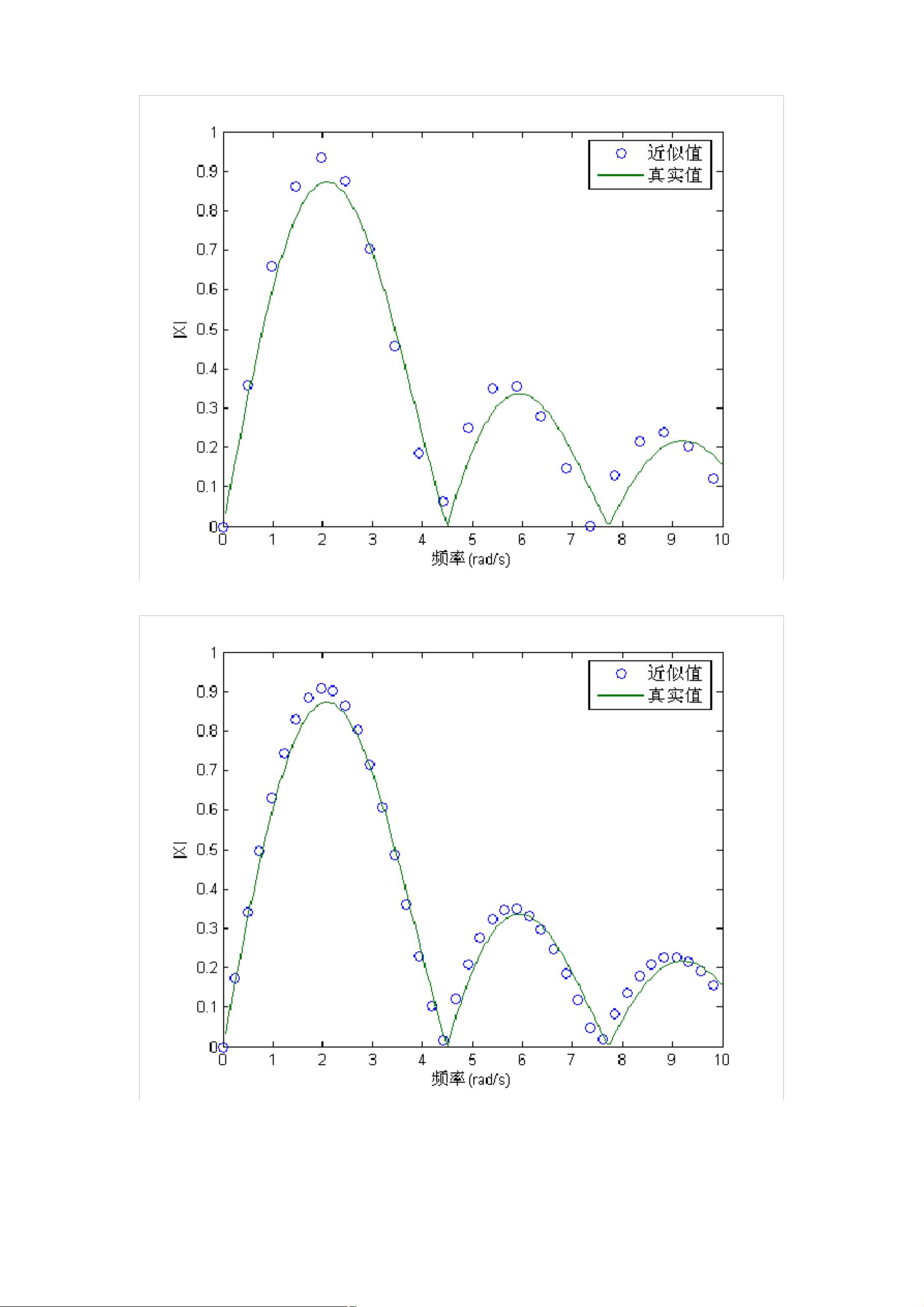当$t<0$时，假设$x(t)=0$，则傅里叶变换可以表示为： $$X(\omega) = \int_{0}^{\infty} x(t)e^{-i\omega t}dt$$ 为了方便计算，可以利用FFT算法来近似计算$X(\omega)$。通过选择适当的时间间隔$T$，使得信号在每个时间间隔内变化较小，我们可以将积分近似为： $$X(\omega) = \sum_{n=0}^{\infty} [e^{-i\omega nT}\int_{nT}^{(n+1)T}x(t)dt] = \sum_{n=0}^{\infty} [e^{-i\omega nT}x(nT)]$$ 当$N$足够大时，对于$n\geq N$的整数，幅值趋于零，我们可以通过FFT算法高效地计算出信号的傅里叶变换。这种方法不仅提高了计算效率，还能保证计算结果的准确性。 总之，傅里叶变换在信号处理中具有重要的应用价值，通过Matlab程序和C语言程序的支持，我们可以方便地对信号进行频域分析，实现更加准确和高效的处理。这些工具为我们提供了强大的计算能力，帮助我们更好地理解和处理各种类型的信号。