8 TeV质子-质子碰撞中压缩质谱场景的顶级夸克对搜索

62 浏览量更新于2024-07-16 收藏 1.21MB PDF 举报

"这篇论文是关于在质子-质子碰撞中使用αT变量搜索压缩质谱场景中顶级夸克对生产的。实验在CERN的大型强子对撞机(LHC)上的CMS探测器进行，数据集对应于18.5 fb^-1的综合光度，中心能量为8 TeV。研究主要目标是寻找超对称性(SUSY)的迹象，特别是通过未观测到的弱相互作用粒子产生的射流和显著的横向动量不平衡(p_Tmiss)。" 在这项研究中，科研团队利用无量纲的运动学变量αT来区分由真实未观测到的粒子导致的p_Tmiss事件和因喷射能量测量误差造成的假阳性p_Tmiss。通过对18.5 fb^-1的数据分析，他们没有发现超出标准模型预期的异常事件。这一结果被用来限制几个简化版的超对称模型，这些模型假设了顶级夸克对的成对产生。研究关注的超对称模型包含了多种顶级squark（t_squark）的衰变模式，包括两体衰变t_squark → cχ_1^0（其中c是魅力夸克，χ_1^0是最轻的中性ino）和四体衰变t_squark → bff'^2χ_1^0（b是底夸克，f和f'^2是W玻色子衰变产生的费米子）。在顶级squark和最轻中性ino质量几乎退化的场景中，这两种衰变模式特别重要。根据这些模式，研究者对二体衰变和四体衰变设定了排除界限，分别为260 GeV和225 GeV的顶级squark质量。这意味着在这些质量范围内，顶级squark的存在与现有数据不符，从而为超对称模型提供了进一步的理论约束。关键词包括CMS（Compact Muon Solenoid），物理学，超对称性，喷流，缺失的横向动量，以及αT变量。这表明研究的核心是通过CMS探测器的数据分析，探索可能存在的超对称现象，并利用αT变量提升识别信号的能力。这篇研究通过在高能碰撞中寻找未观测到的粒子的迹象，提供了对超对称理论的测试和限制，特别是在压缩质谱场景下顶级夸克对的生产。实验结果加深了我们对标准模型之外可能的新物理现象的理解，并为未来的粒子物理学研究提供了有价值的参考。

408 The CMS Collaboration / Physics Letters B 767 (2017) 403–430

and H

miss

[90], although the acceptances differ. An advantage of

the γ + jets process is its much larger production cross section

compared to the Z → νν +jets process.

In the case of events with N

≥ 2, the μ + jets sample is also

used to estimate the small Z → νν + jets background because of

the limited event counts in the μμ +jets and γ +jets control sam-

ples.

The method relies on the use of W → μν +jets events to pre-

dict

the Z →μμ +jets background [25,27,28]. The method corrects

for tt contamination in the μ + jets sample, which can be signiﬁ-

cant

in the presence of jets identiﬁed as originating from b quarks.

However, while the tt contamination increases with increasing N

the Z → μμ +jets background is reduced to a sub-dominant level

relative to other backgrounds. The method is validated in data con-

trol

regions deﬁned by samples of events categorised according to

. In summary, only the μ + jets sample is used to estimate the

total SM background for events with N

≥2, whereas all three data

control samples are used for events with N

≤1.

To maximise sensitivity to new-physics signatures with a large

number of b quarks, a method is employed that allows event yields

for a given b quark jet multiplicity to be predicted with a higher

statistical precision than obtained directly from simulation, partic-

ularly

for events with a large number of b quark jets (N

≥2) [28].

The method relies on generator-level information contained in the

simulation to determine the distribution of N

for a sample of

events categorised according to N

jet

and H

. First, simulated events

are categorised according to the number of jets per event that

are matched to underlying b quarks (N

gen

), c quarks (N

gen

), and

light-ﬂavoured quarks or gluons (N

gen

). Second, the eﬃciency 

with which b quark jets are identiﬁed, and the misidentiﬁcation

probabilities for c quarks and light-ﬂavour partons, f

and f

, re-

spectively,

are also determined from simulation, with each quantity

averaged over jet p

and η per event category. Corrections to ,

, and f

are applied on a jet-by-jet basis as a function of p

and η so that they match the corresponding quantity measured in

data [71]. Finally, N

tag

, N

tag

, and N

tag

are, respectively, the num-

ber

of jets identiﬁed (“tagged”) as originating from b quarks per

event when the underlying parton is a b quark, c quark, or a light-

ﬂavoured

quark or gluon, and P(N

tag

; N

gen

, ), P(N

tag

; N

gen

, f

and P(N

tag

; N

gen

, f

) are the binomial probabilities for this to hap-

pen.

These quantities are suﬃcient to estimate how events are

distributed according to N

per (N

jet

, H

) category when sum-

ming

over all relevant combinations that satisfy the requirements

jet

= N

gen

+ N

gen

+ N

gen

and N

= N

tag

+ N

tag

+ N

tag

The

event yields determined with the method described above

are subsequently used to determine the transfer factors binned ac-

cording

to N

(in addition to N

jet

and H

). The uncertainties in the

transfer factors obtained from simulation are evaluated through

sets of closure tests based on events from the data control re-

gions [28].

Each set uses the observed event counts in up to eleven

bins in H

for a given sample of events, along with the corre-

sponding

-dependent) transfer factors obtained from simula-

tion,

to determine H

-dependent predictions N

pred

) for yields

in another event sample. The two samples are taken from differ-

ent

data control regions, or are subsets of the same data control

sample with differing requirements on N

jet

or N

. The predic-

tions

pred

) are compared with the H

-binned observed yields

obs

) and the level of closure is deﬁned by the deviation of

the ratio (N

obs

− N

pred

)/N

pred

from zero. A large number of tests

are performed to probe key aspects of the modelling that may in-

troduce

an N

jet

-or H

-dependent source of bias in the transfer

factors [28].

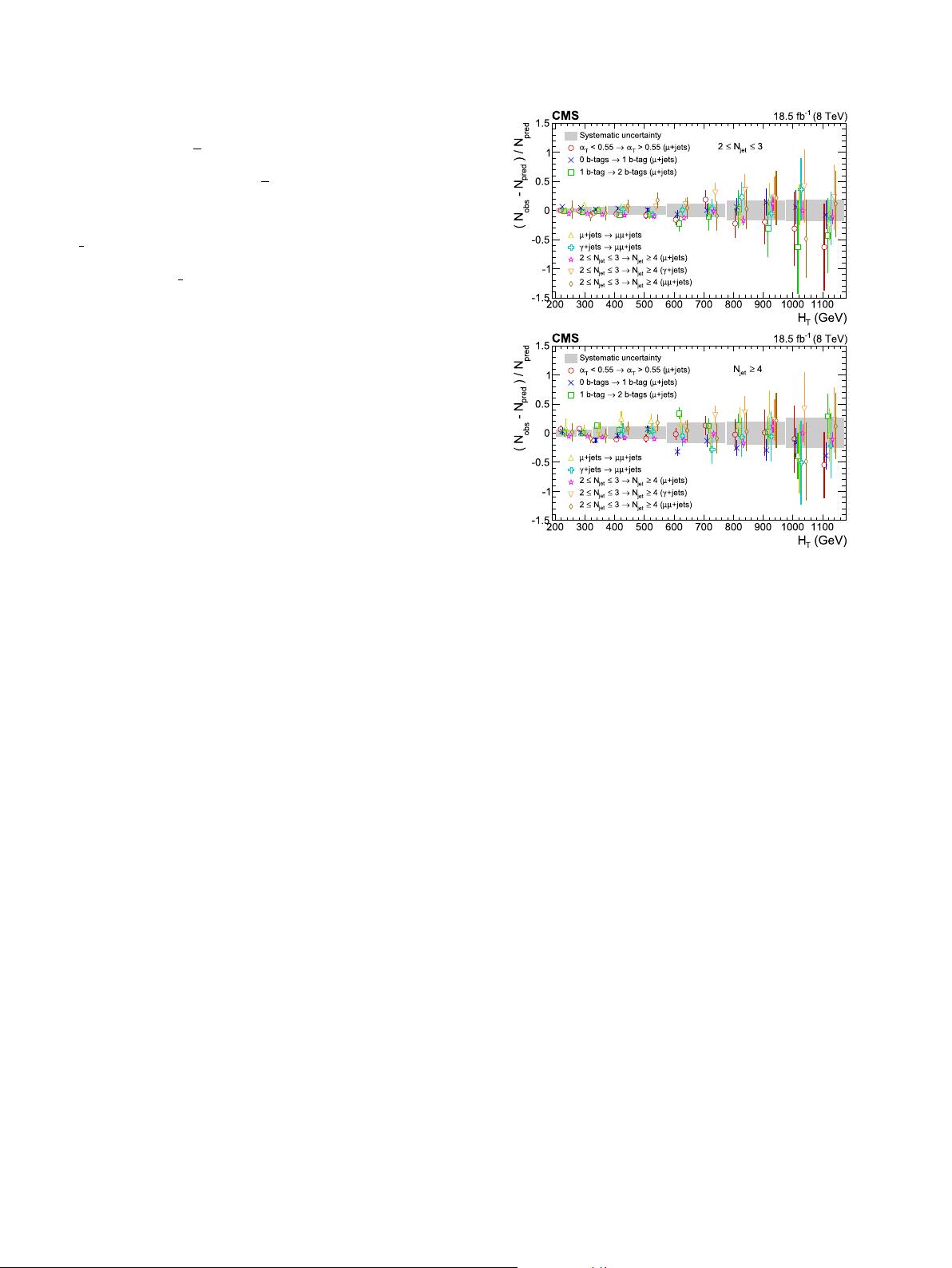
Systematic

uncertainties are determined from core sets of clo-

sure

tests, of which the results are shown in Fig. 2. Five sets of

tests are performed independently for each of the two N

jet

cat-

egories,

and a further three sets that are common to both N

jet

Fig. 2. Ratio (N

obs

− N

pred

)/N

pred

as a function of H

for different event categories

and/or control regions for (upper) events with two or three jets, and (lower) events

with four or more jets; “b tag” refers to a reconstructed b quark candidate. Error

bars represent statistical uncertainties only, while the grey shaded bands represent

the N

jet

-and H

-dependent uncertainties assumed in the transfer factors, as deter-

mined

from the procedure described in the text.

categories. The tests aim to probe for the presence of statistically

signiﬁcant biases that could arise due to limitations in the method.

For each N

jet

category, the ﬁrst three sets of closure tests are per-

formed

using the μ + jets sample. The ﬁrst set probes the mod-

elling

of the α

distribution for events containing genuine



miss

from neutrinos (open circle markers). Two sets (crosses, squares)

probe the relative composition between W + jets and top events

and the modelling of the reconstruction of b quark jets. The fourth

set (triangles) validates the modelling of vector boson production

by connecting the μ + jets and μμ +jets control samples, which

are enriched in W + jets and Z + jets events, respectively. The

ﬁfth set (swiss crosses) deals with the consistency between the

γ + jets and μμ + jets samples, which are both used to provide

an estimate of the Z → μμ + jets background. Three further sets

of closure tests (stars, inverted triangles, diamonds), one per data

control sample, probe the simulation modelling of the N

jet

distri-

bution

for a range of background compositions.

The

closure tests reveal no signiﬁcant biases or dependency on

jet

nor H

. Systematic uncertainties in the transfer factors are

determined from the variance in (N

obs

− N

pred

)/N

pred

, weighted

to account for statistical uncertainties, for all closure tests within

an individual H

bin in the range 200 < H

< 375 GeV and for

each N

jet

category. For the region H

> 375 GeV, all tests within

200 GeV-wide intervals in H

, deﬁned by pairs of adjacent bins,

are combined to determine the systematic uncertainty, which is as-

sumed

to be fully correlated for bins within each interval, and fully

uncorrelated for different H

intervals and N

jet

categories. The

magnitudes of the systematic uncertainties are indicated by shaded

grey bands in Fig. 2 and summarised in Table 2. The same (uncor-

related)

value of systematic uncertainty is assumed for each N

category. An independent study is performed to assess the effect

of uncertainties in the simulation modelling of the eﬃciency and

剩余27页未读，继续阅读

weixin_38628953

粉丝: 6
资源: 926

8 TeV质子-质子碰撞中压缩质谱场景的顶级夸克对搜索

在s = 13 TeV质子-质子碰撞中单顶夸克和光子的联合产生的证据

在s = 8 TeV的质子-质子碰撞中搜索γ+ jet最终状态中激发的夸克

在s = 8 TeV的质子-质子碰撞中的b标记Dijet质谱中搜索窄共振

在s = 13 TeV的质子-质子碰撞中搜索四个顶级夸克的标准模型生产

在s = 8 TeV的质子-质子碰撞中使用单个顶夸克事件测量顶夸克质量

在s = 13 TeV的质子-质子碰撞中搜索衰变成夸克-反夸克对的低质量矢量共振

使用ATLAS探测器搜索在s = 8TeV的质子-质子碰撞中与单顶夸克相关的不可见粒子

s = 33TeV和s = 100TeV质子-质子超级对撞机的受约束超对称前景

使用s = 13 TeV质子-质子碰撞，利用ATLAS搜索具有大射流多重性且缺少横向动量的最终状态中的新现象

在s = 13 TeV的质子-质子碰撞中搜索耦合到第三代夸克的Le夸克

最新资源