0885-8993 (c) 2016 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TPEL.2017.2693383, IEEE
Transactions on Power Electronics
IEEE TRANSACTION ON POWER ELECTRONICS
It should be noted that frequency adjustments would be
executed at every current zero-crossing point; therefore,
resonance tracking would be accomplished within one half of a
resonance cycle. However, a tracking error always exists
between the resonance and the damped natural frequency, and
this error will be evaluated in the next section.
B. Tracking Error Analysis in Unloaded Model
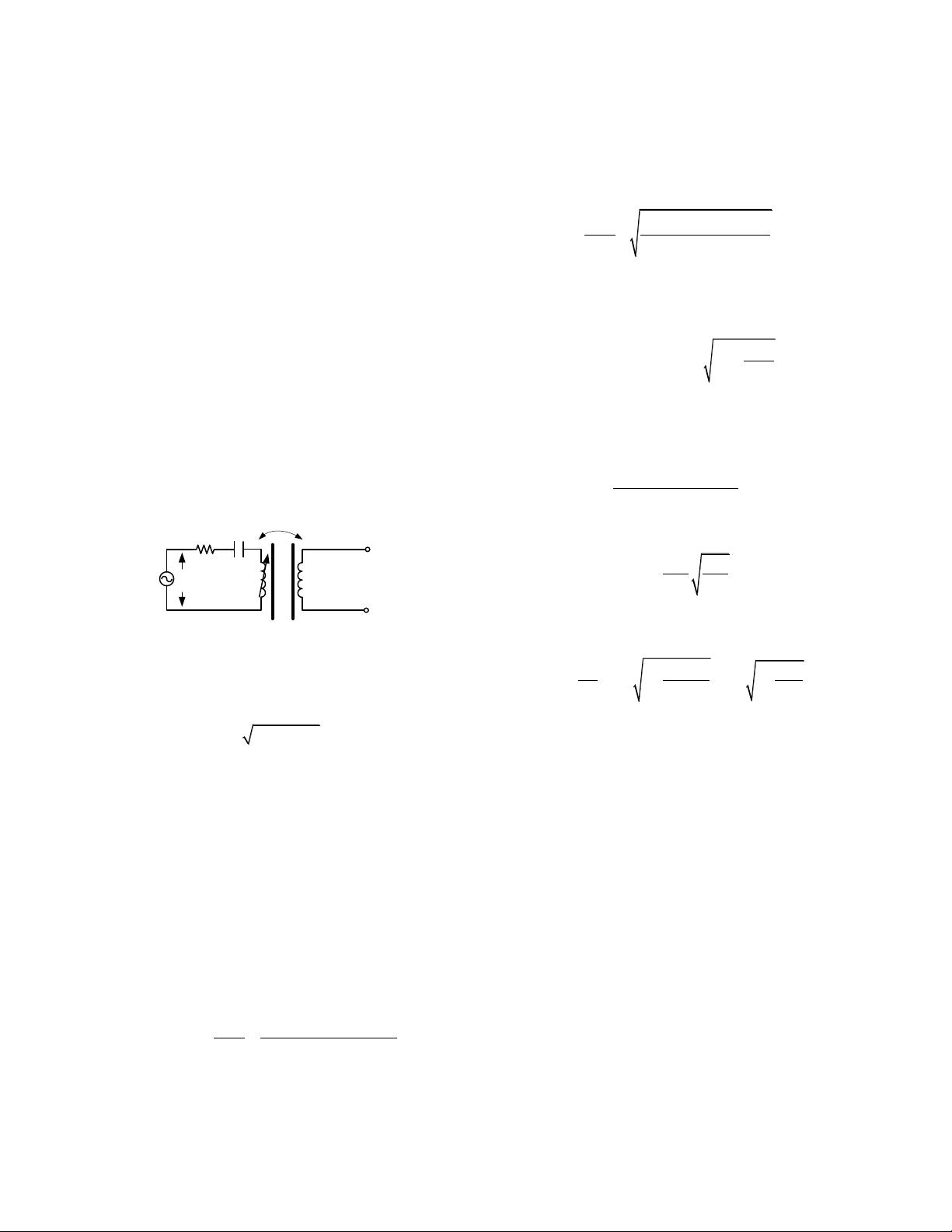
A simplified circuit model of a resonant ICPT system is
shown in Fig. 3. An AC chopper provides the power to be
transmitted to the receiver at an operating frequency of ω. The
transmitter is then configured in the form of a series resonant
loop to compensate the loosely coupled coils, where L
TX
is the
transmitting coil inductance, C
TX
is the series resonant
capacitor, and R
TX
is the total resistive loss, including the
source resistance, the radiation loss resistance, and the ESR
values of both the transmitting coil and the resonant capacitor.
Both transmitting and receiving coils are wounded on ferrite
core to increase the coupling coefficient K between them, the
displacement between the two coils would change the
equivalent inductance of L
TX
and will thus ultimately affect the
resonance frequency.
Transmitter
Receiver
K
V
s
R
TX
C
TX
L
TX
L
RX
Fig. 3. Circuit model of light-load ICPT system.
The resonance frequency is then given by
(4)
The maximum induction voltage will be obtained in the
secondary coil when ω=ω
0
. The proposed tracking method will
track the damped natural frequency, and thus the difference
between the resonance frequency ω
0
and the damped natural
frequency ω
f
is investigated.
In the transmission loop, Kirchhoff’s voltage law (KVL)
equation is given by:
(1/ )
TX TX TX TX S
sC R sL I V
, (5)
where s is the complex number of the frequency parameter and
I
TX
is the loop current, which can be expressed as:
2
()
()
( ) 1
TX s
TX
TX TX TX TX
C sV
Ns
Is
D s s C L sC R
. (6)
The natural response of the system is therefore directly
determined by the roots of the denominator of Equation (6),
regardless of the input and the initial conditions of the circuit.
The characteristic equation is formulated as
2
(1 0)
TX TX TX TX
D s C R s C L s
2
{
4
2
1,2
2
}.
k
TX TX TX TX
TX
TX TX TX
C R C L
L C L
k
R
(8)
ω
f
is determined by the imaginary part of these roots.
Therefore, it is given by
,
2
2
2
1 2 0
Im( )
4
T
f
X
TX
R
L
(9)
The oscillation maintaining condition of the transmitting
loop is obtained as:
2
4
0
2
TX TX TX TX
TX TX
C R C L
CL
, (10)
which is simplified to read
. (11)
Q is the quality factor of the resonance loop. The tracking
error is evaluated in the form
2
2
1
1 1 11
4
1
4
TX TX
TX
o
f
RC
QL
. (12)
Equation (9) indicates that the tracking error is solely
determined by the quality factor of the resonance loop. A
tracking error of less than 1% only requires Q > 3.6. The typical
quality factor of a general ICPT transmitter is more than 20; this
guarantees a tracking error of less than 0.12%, which is almost
negligible. This proves that the proposed method could be used
to track the resonance frequency of the ICPT.
C. Tracking Error Analysis in Loaded Model
A more practical scenario involves taking the secondary load
into consideration, as shown in Fig. 4(a). In this case, the
resistance load of the receiver is considered and the receiver
loop can be regarded as the reflected impedance Z
REF
in the
resonance loop, as shown in Fig. 4(b). Both movement between
the ferrite components and a change in the load would change
the resonance frequency under these circumstances.
The resonance frequency can be determined using the loop
impedance,
, (13)
which is the sum of the transmitter impedance Z
TX
and the
reflected impedance of the receiver, Z
REF
, where





































