三级放大器频率补偿深度分析与改进策略

4星 · 超过85%的资源需积分: 49 16 浏览量更新于2024-07-31 1 收藏 365KB PDF 举报

本文主要探讨了三级放大器的频率补偿技术，发表在2001年9月的《IEEE Transactions on Circuits and Systems - I: Fundamental Theory and Applications》上。作者Ka-Nang Leung和Philip K. T. Mok是IEEE成员，他们重新分析了单级、双级和三级放大器的频率补偿方法，这些方法基于Miller极点分裂和极点零点消除。文章首先概述了频率补偿技术的重要性，尤其是在多级放大器设计中的应用，由于技术的进步，对单级cascode放大器等多级结构的需求日益增长。作者详细地讨论了所采用的假设、传递函数、稳定性的评估标准、带宽以及各种报道过的设计问题。研究重点包括但不限于： 1. **Miller极点补偿**：这是一种常见的频率补偿策略，通过在放大器电路中引入额外的反馈路径，可以有效地改变放大器的高频特性，以抵消由于晶体管增益随着频率升高而减小的影响，从而保持增益稳定性。 2. **多路径nested Miller补偿**：这种方法涉及在多个反馈路径中实施Miller补偿，每个路径都有其独特的频率响应，以实现更精确的频率补偿。 3. **多路径零点消除**：通过调整电路参数，使得放大器在特定频率点的零点被消除，有助于减少谐波失真和提高放大器的线性性能。 4. **多级放大器的nested Gm-C补偿**：这是一种利用共集电极-电容（Gm-C）网络来改善多级放大器频率响应的技术，通过对各级放大器进行局部补偿，提高整体系统的稳定性。 5. **简单Miller补偿**：尽管名称简单，这种补偿方法可能是初级阶段的，但仍可能在某些特定的应用场景下有效。文章不仅理论分析深入，还提供了模拟仿真和实验结果，以验证所提出的改进方法的有效性和实用性。关键词包括：阻尼因子控制频率补偿、多重路径嵌套Miller补偿、多重路径零点消除、多级放大器和嵌套Miller补偿。本文为设计工程师提供了一套全面的频率补偿策略，对于理解和优化多级放大器设计具有重要意义。

1044 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—I: FUNDAMENTAL THEORY AND APPLICATIONS, VOL. 48, NO. 9, SEPTEMBER 2001

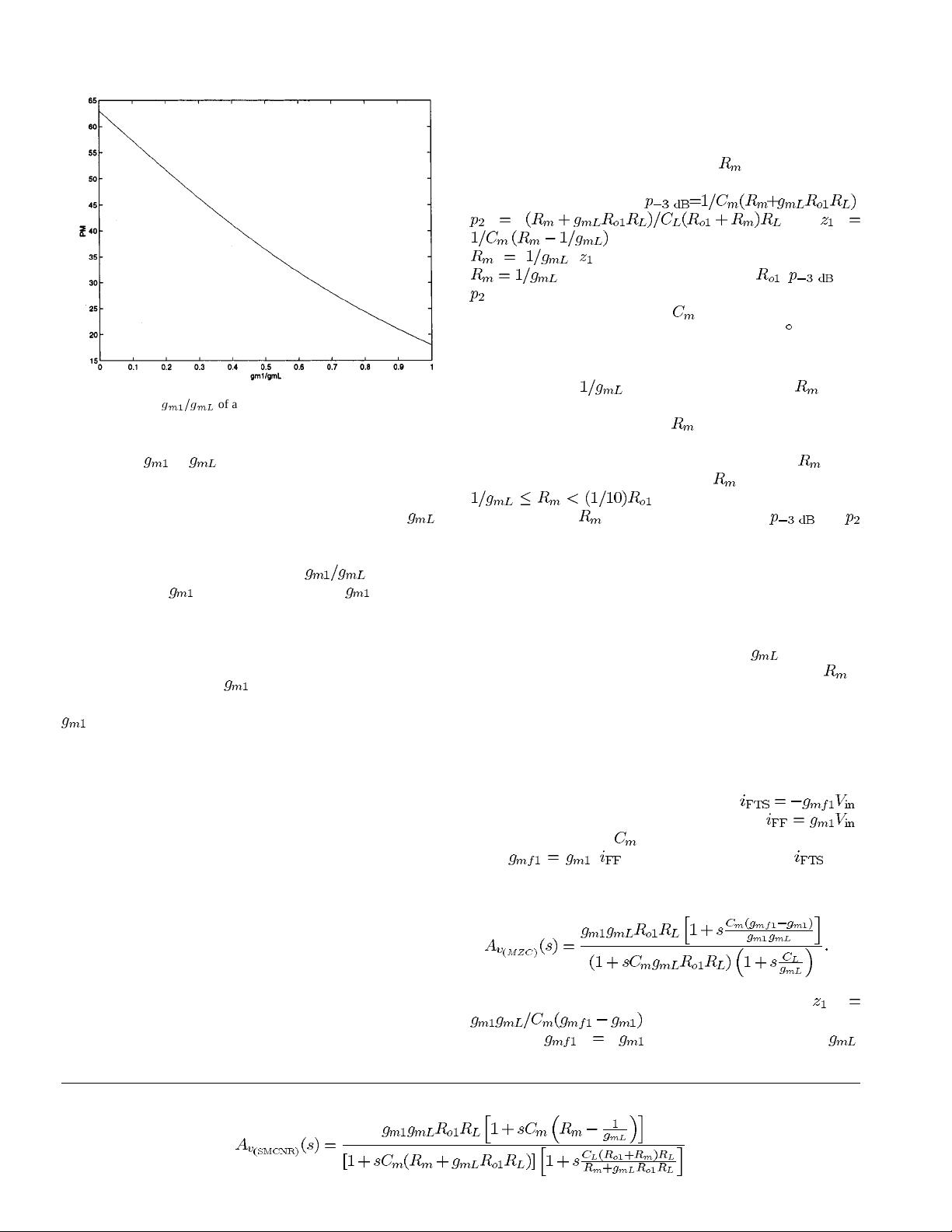
Fig. 3. PM versus

g =g

of a SMC amplifier.

From (6) and Fig. 3, the PM of a SMC amplifier strongly de-

pends on the

to ratio and this, in fact, shows the RHP

zero effect on the PM. Physically, the presence of the RHP zero

is due to the feedforward small-signal current flowing through

the compensation capacitor to the output [1]–[11]. If

large, the small-signal output current is larger than the feed-

forward current and the effect of the RHP zero appears only

at very high frequencies. Thus, a small

gives a better

PM, so a smaller

is preferable. However, is limited by

the bias current and size of the input differential pair. To have

a good slew rate, the bias current cannot be small. In addition,

to have a small offset voltage, the size of input differential pair

cannot be too small. Emitter/source degeneration technique is

also not feasible to reduce

since it reduces the limited input

common-mode range in low-voltage design. Therefore, a small

cannot be obtained easily.

From the previous analysis, it is known that the RHP zero

degrades the stability significantly. There are many methods

to eliminate the RHP zero and improve the bandwidth. The

methods involve using voltage buffer [4]–[6] and current buffer

[7], [8], a nulling resistor [2], [3], [9]–[11], and MZC technique

[12]. In this paper, the techniques to be discussed are: 1) SMC

using nulling resistor (SMCNR) and 2) SMC using MZC.

A. SMCNR

The presence of the RHP zero is due to the feedforward small-

signal current. One method for reducing the feedforward current

and thus eliminating the RHP zero is to increase the impedance

of the capacitive path. This can be done by inserting a resistor,

called nulling resistor, in series with the compensation capacitor,

as shown in Fig. 1(b). Most published analyses only focus on the

effect of the nulling resistor to the position of the zero but not

to the positions of the poles. In fact, when the nulling resistor is

increased to infinity, the compensation network is open-circuit

and no pole splitting takes place. Thus, the target of this section

is to investigate the limit of the nulling resistor.

The transfer function of the SMNCR (

), is as shown as (7)

at the bottom of the page. Now, the dominant pole, nondominant

pole and zero are given by

and

, respectively. It is well-known that when

, is completely eliminated. In addition, as

is generally much smaller than , and

are approximately the same as in SMC without the nulling

resistor. Therefore, the value of

is determined by (4). The

GBW is also given by (5) and the PM is about 63

due to the

absence of the RHP zero.

However, many designers prefer to use a nulling resistor with

value larger than

since an accurate value of is dif-

ficult to obtain and a LHP zero, which increases the PM, is

created. In fact, from (7), when

is increased, the positions

of the poles will be changed accordingly and moved to lower

frequencies. The pole-splitting effect is destroyed if

is too

large. In other words, there is a limit of

and suggested to be

. This upper limit is based on the

compromise that

in both the expressions of and

are negligible.

B. SMC Using MZC

In many high-performance two-stage amplifiersdrivingresis-

tive load, a Class-AB output stage is used to obtain a good con-

trol of the quiescent-to-maximum output current ratio. Since the

output current changes during the operation,

is not a con-

stant and a precise cancellation of the RHP zero by a fixed

not possible. The amplifier may not be stable at certain output

current level, so SMC using MZC was introduced [12]. MZC

is a simple but effective method to eliminate the RHP zero. It

has an additional advantage that the positions of the poles are

not affected by the additional circuitry. As shown in Fig. 1(c), a

feedforward transconductance stage (FTS) is added and it pro-

duces an out-of-phase small-signal current (

)

to cancel the feedforward small-signal current (

)

which passes through

at high frequencies. Theoretically,

when

, is completely canceled by . This

can be shown by the transfer function

(8)

From the transfer function, the cancellation of

is achieved, as stated before,

by setting

, which is independent of .

(7)

Authorized licensed use limited to: Peking University. Downloaded on August 11, 2009 at 04:48 from IEEE Xplore. Restrictions apply.

剩余15页未读，继续阅读

whdm2008

粉丝: 0
资源: 5

三级放大器频率补偿深度分析与改进策略

III型补偿误差放大器 双零点双极点合集补充

LDO的核心误差放大器的简介和频率补偿的分析和设计-综合文档

运算放大器

宽带放大器 AD603

工程师运算放大器应用指南

深入解析如何选择仪表放大器

2003年索尼杯宽带放大器

低电压下使用基本运算放大器的设计技巧

美国国家半导体推出业界最低噪声的超高速放大器 (1).pdf

高精度电压频率转换器芯片设计

最新资源

III型补偿误差放大器双零点双极点合集补充