LLC谐振半桥功率转换器设计：高效与复杂性的权衡

需积分: 23 167 浏览量更新于2024-07-18 收藏 1.21MB PDF 举报

在现代电源供应设计中，对效率、功率密度和组件紧凑性的追求日益增长。TI的LLC（Laminated-Layered-Combined）半桥谐振功率转换器因其在高电压输入场合能实现更高的转换效率而备受关注，这种设计方法通常用于中等功率隔离应用中，以克服传统半桥架构在效率提升时所面临的复杂性。LLC配置采用两个互感器（L）和一个电容器（C），形成独特的电路结构，它能够显著提升系统性能。设计一个LLC谐振半桥转换器的关键在于理解其工作原理。首先，这种设计利用了频率调制特性，通过一种称为第一谐波近似（First Harmonic Approximation, FHA）的独特分析工具来控制。FHA是一种简化模型，它允许工程师精确定义电路参数，并预测转换器在不同负载条件下的行为。通过FHA，设计师可以优化开关频率、电感值、电容值以及控制回路，以实现最佳的功率转换效率和动态响应。设计过程中，必须考虑以下重要因素： 1. **电路参数选择**：合适的电感（L）和电容（C）值是决定谐振频率和工作带宽的关键，它们决定了转换器的Q值，进而影响了转换效率和纹波性能。 2. **频率调制策略**：FHA有助于确定在不同负载变化时如何调整频率，以保持或优化效率。这可能涉及在轻载时提高频率以减小开关损耗，在重载时降低频率以保持输出稳定。 3. **开关元件**：选择合适的开关器件，如IGBT或MOSFET，要考虑其开关速度、驱动要求以及对高频操作的承受能力，以确保转换器能在高效率下运行。 4. **热管理**：由于高频工作，散热成为关键问题。设计者需要计算和优化散热路径，以防止过热并延长转换器的使用寿命。 5. **电磁兼容性和噪声抑制**：LLC谐振转换器产生的电磁干扰可能对系统其他部分造成影响，因此需要设计有效的EMI滤波器和噪声抑制措施。 6. **实验室验证**：设计完成后，全面的实验室测试是必不可少的，以验证理论分析结果与实际性能的一致性，包括测量效率、输出电压和电流、以及转换速率响应等指标。设计一个高效的TI LLC半桥谐振功率转换器需要深入了解电路原理、利用FHA进行精确分析，以及在实际应用中平衡复杂性与性能。通过优化这些要素，设计师可以满足现代电源系统对高效、紧凑和可靠性的需求。

3-6

Topic 3

Traditional Modeling Methods Do Not Work Well

To develop a transfer function, all variables

should be defined by equations governed by the

LLC converter topology shown in Fig. 5a. These

equations are then solved to get the transfer

function. Conventional methods such as state-

space averaging have been successfully used in

modeling pulse-width-modulated switching

converters, but from a practical viewpoint they

have proved unsuccessful with resonant converters,

forcing designers to seek different approaches.

Modeling with Approximations

As already mentioned, the LLC converter is

operated in the vicinity of series resonance. This

means that the main composite of circulating

current in the resonant network is at or close to the

series resonant frequency. This provides a hint that

the circulating current consists mainly of a single

frequency and is a pure sinusoidal current.

Although this assumption is not completely

accurate, it is close—especially when the square

wave’s switching cycle corresponds to the series

resonant frequency. But what about the errors?

If the square wave is different from the series

resonance, then in reality more frequency

components are included; but an approximation

using the single fundamental harmonic of the

square wave can be made while ignoring all higher-

order harmonics and setting possible accuracy

issues aside for the moment. This is the so-called

first harmonic approximation (FHA) method, now

widely used for resonant-converter design. This

method produces acceptable design results as long

as the converter operates at or close to the series

resonance.

The FHA method can be used to develop the

gain, or the input-to-output voltage-transfer

function. The first steps in this process are as

follows:

Represent the primary-input unipolar square- •

wave voltage and current with their funda men tal

components, ignoring all higher-order

harmonics.

Ignore the effect from the output capacitor and •

the transformer’s secondary-side leakage

inductance.

Refer the obtained secondary-side variables to •

the primary side.

Represent the referred secondary voltage, which •

is the bipolar square-wave voltage (V

), and the

referred secondary current with only their

fundamental components, again ignoring all

higher-order harmonics.

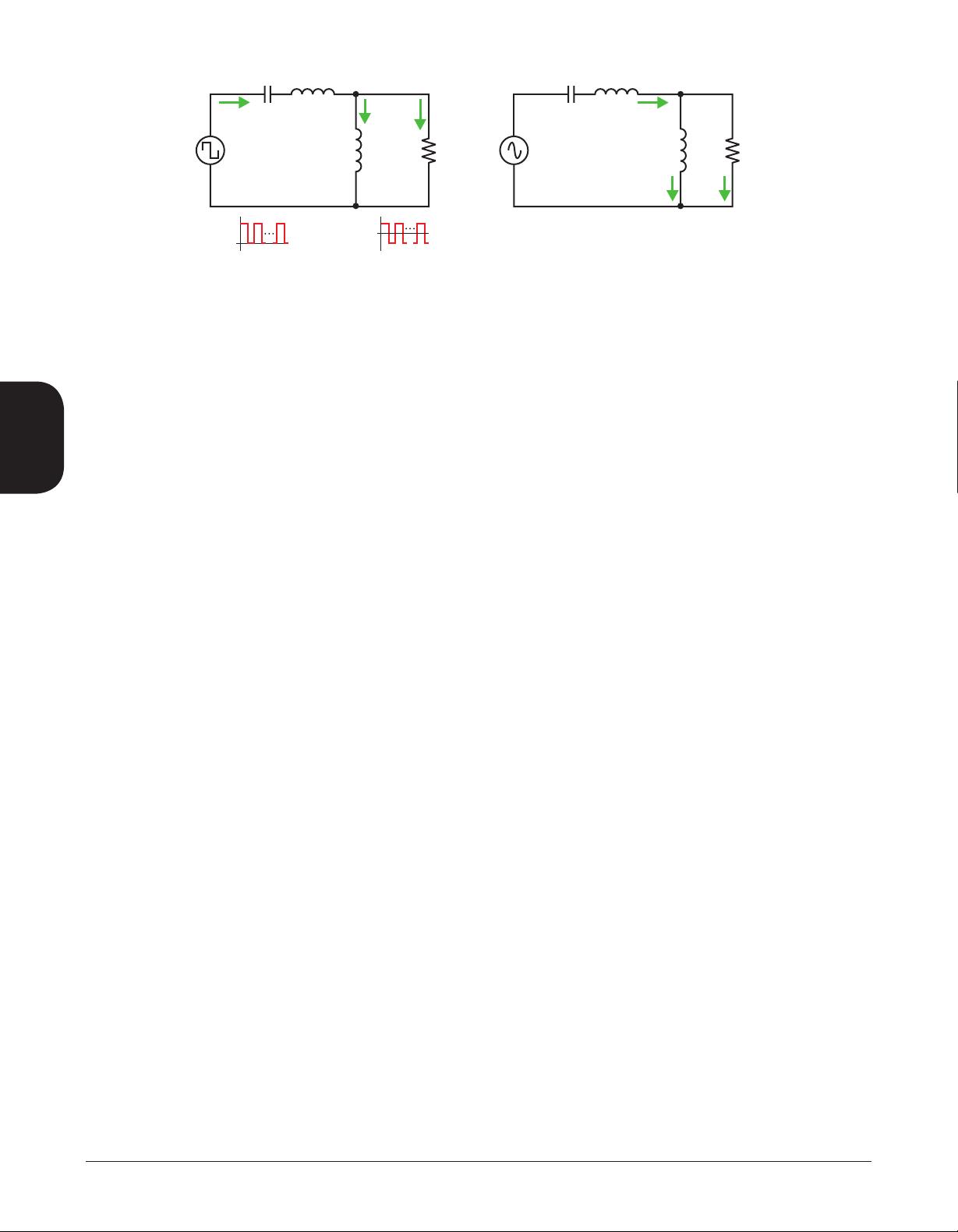
With these steps accomplished, a circuit model

of the LLC resonant half-bridge converter in Fig.

5a can be obtained (Fig. 5b). In Fig. 5b, V

is the

fun damental component of V

, and V

is the fun-

damental component of V

. Thus, the non linear

and nonsinusoidal circuit in Fig. 5a is approx i-

mately transformed into the linear circuit of Fig.

5b, where the AC resonant circuit is excited by an

effective sinusoidal input source and drives an

equivalent resistive load. In this circuit model,

both input voltage V

and output voltage V

are

in sinusoidal form with the same single frequency—

i.e., the fundamental component of the square-

wave voltage (V

), generated by the switching

operation of Q1 and Q2.

This model is called the resonant converter’s

FHA circuit model. It forms the basis for the

Fig. 5. Model of LLC resonant half-bridge converter.

–

R´

a. Nonlinear nonsinusoidal circuit.

b. Linear sinusoidal circuit.

剩余26页未读，继续阅读

xjxj2

粉丝: 0
资源: 7

LLC谐振半桥功率转换器设计：高效与复杂性的权衡

llc TI 设计例程

参考资料-LLC 英飞凌.zip

通信电源电路图

大厂的LLC设计资料，很详细的设计

4kW+数字LLC设计资料.rar

4kW+数字LLC设计资料深度解析

电力电子电源设计系列LLC教程LLC设计技术资料文档资料合集（140个）.zip

LLC培训资料+设计步骤

LLC经典资料

参考资料-LLC设计步骤.zip

最新资源