"梯度下降法解决线性回归问题PPT1"
需积分: 0 65 浏览量
更新于2024-04-11
收藏 1.82MB PDF 举报
本段描述主要介绍了在线性回归问题中使用梯度下降法进行求解的相关内容。通过中国大学MOOC的PPT1课件,详细讲解了梯度下降法在线性回归中的应用。梯度下降法是一种常用的优化算法,通过不断迭代更新参数来最小化损失函数,从而得到最优的模型参数。本课程通过大量的实例演示和计算细节说明了梯度下降法的原理和实现步骤。
首先,PPT1介绍了线性回归问题的基本概念,包括目标函数、损失函数和梯度下降法的核心思想。线性回归是一种用于预测连续变量的机器学习算法,其目标是找到一条最适合数据分布的直线,使得预测值与真实值之间的误差最小化。损失函数是衡量模型预测结果与真实值之间差异的函数,通常使用平方误差作为损失函数。梯度下降法是一种迭代优化算法,通过计算损失函数关于模型参数的梯度,不断更新参数以减小损失函数的值。
其次,PPT1详细介绍了梯度下降法的步骤和算法原理。梯度下降法分为批量梯度下降、随机梯度下降和小批量梯度下降三种不同的方式。批量梯度下降在每一次迭代中都要使用全体数据进行计算,计算量大但能得到精确的结果;随机梯度下降每次迭代只使用一个样本来计算梯度,计算速度快但有一定的随机性;小批量梯度下降是批量梯度下降和随机梯度下降的折中方案,使用一部分样本进行计算,可以兼顾计算量和计算精度。
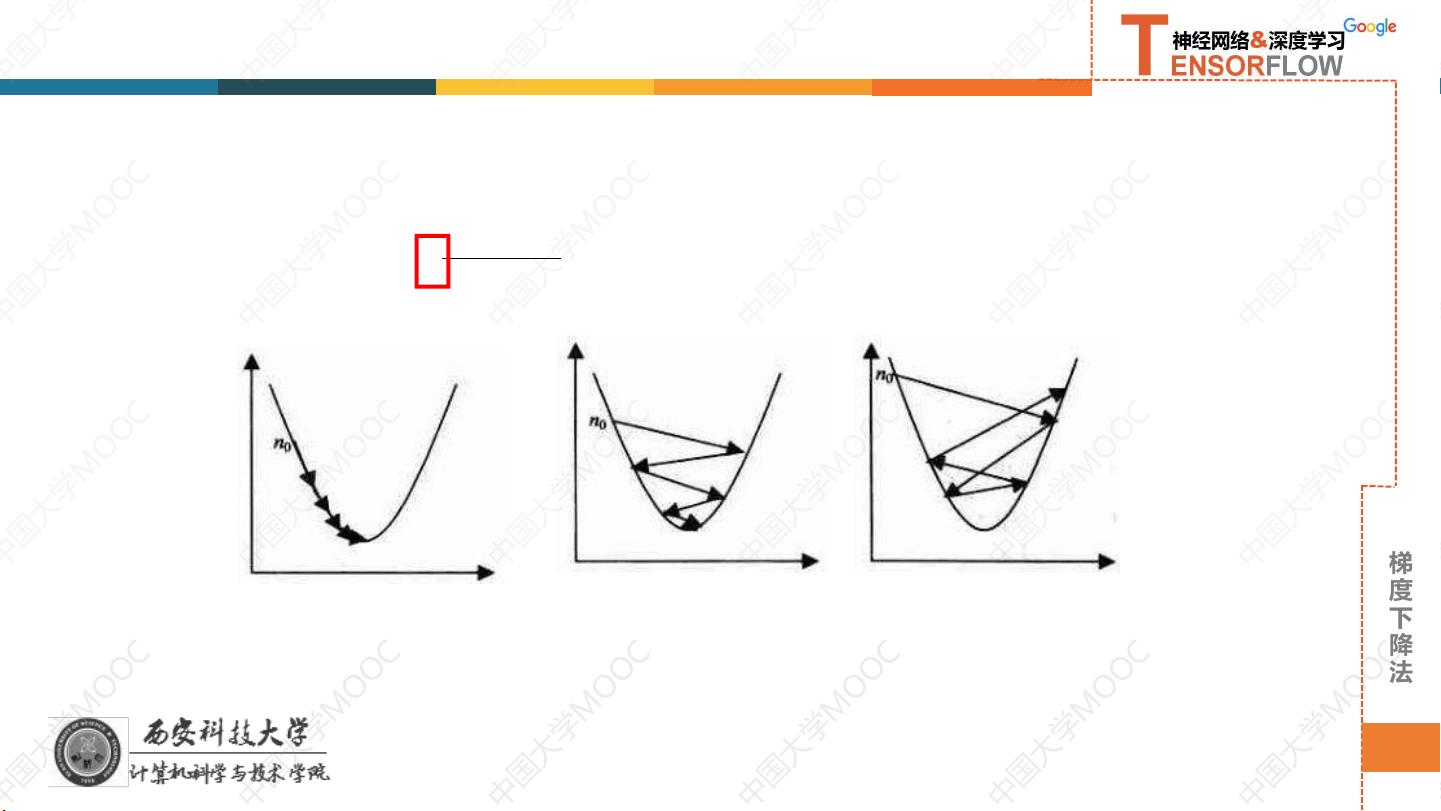
最后,PPT1通过具体的数学推导和实例演示了梯度下降法在线性回归中的应用。通过不断迭代更新参数,最终得到使损失函数最小化的最优参数组合。此外,PPT1还介绍了梯度下降法的收敛性、学习率的选取、超参数的调节等相关内容,帮助学员更好地理解和应用梯度下降法求解线性回归问题。
综上所述,通过中国大学MOOC的PPT1课件,我们详细学习了梯度下降法在线性回归中的原理和应用。梯度下降法作为一种常用的优化算法,在机器学习和深度学习领域具有重要的意义,掌握梯度下降法的原理和实现步骤对于深入理解模型优化和参数调节具有重要意义。通过学习和实践,我们可以更好地掌握梯度下降法的应用,提高模型的准确性和泛化能力。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2019-04-22 上传
2023-11-10 上传
2021-01-28 上传
Period熹微
- 粉丝: 30
- 资源: 307
最新资源
- WordPress作为新闻管理面板的实现指南
- NPC_Generator:使用Ruby打造的游戏角色生成器
- MATLAB实现变邻域搜索算法源码解析
- 探索C++并行编程:使用INTEL TBB的项目实践
- 玫枫跟打器:网页版五笔打字工具,提升macOS打字效率
- 萨尔塔·阿萨尔·希塔斯:SATINDER项目解析
- 掌握变邻域搜索算法:MATLAB代码实践
- saaraansh: 简化法律文档,打破语言障碍的智能应用
- 探索牛角交友盲盒系统:PHP开源交友平台的新选择
- 探索Nullfactory-SSRSExtensions: 强化SQL Server报告服务
- Lotide:一套JavaScript实用工具库的深度解析
- 利用Aurelia 2脚手架搭建新项目的快速指南
- 变邻域搜索算法Matlab实现教程
- 实战指南:构建高效ES+Redis+MySQL架构解决方案
- GitHub Pages入门模板快速启动指南
- NeonClock遗产版:包名更迭与应用更新