"云计算下的快速PQ分解法在潮流计算中的应用研究"
版权申诉
65 浏览量
更新于2024-04-03
收藏 1.22MB PDF 举报
Abstract
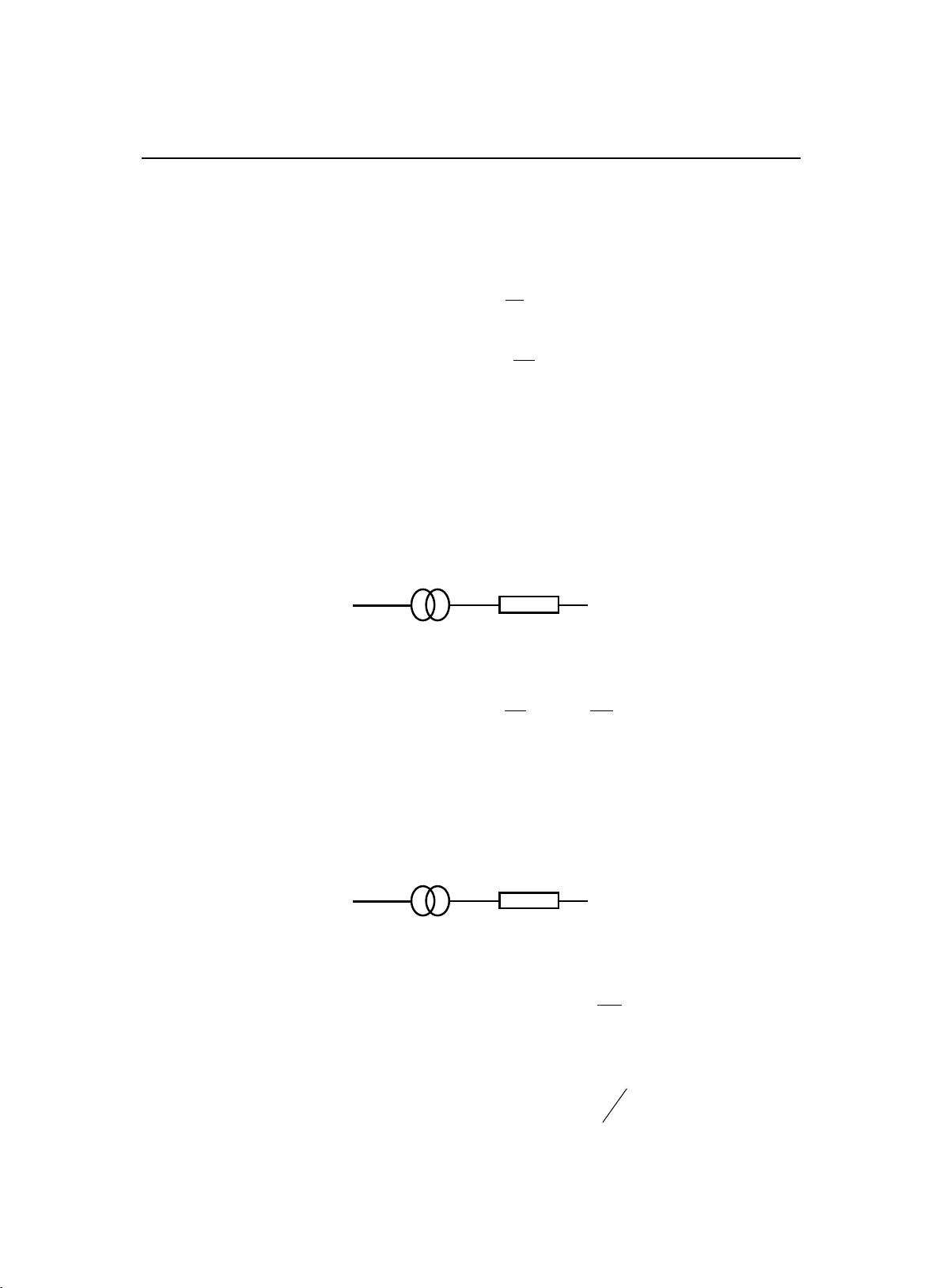
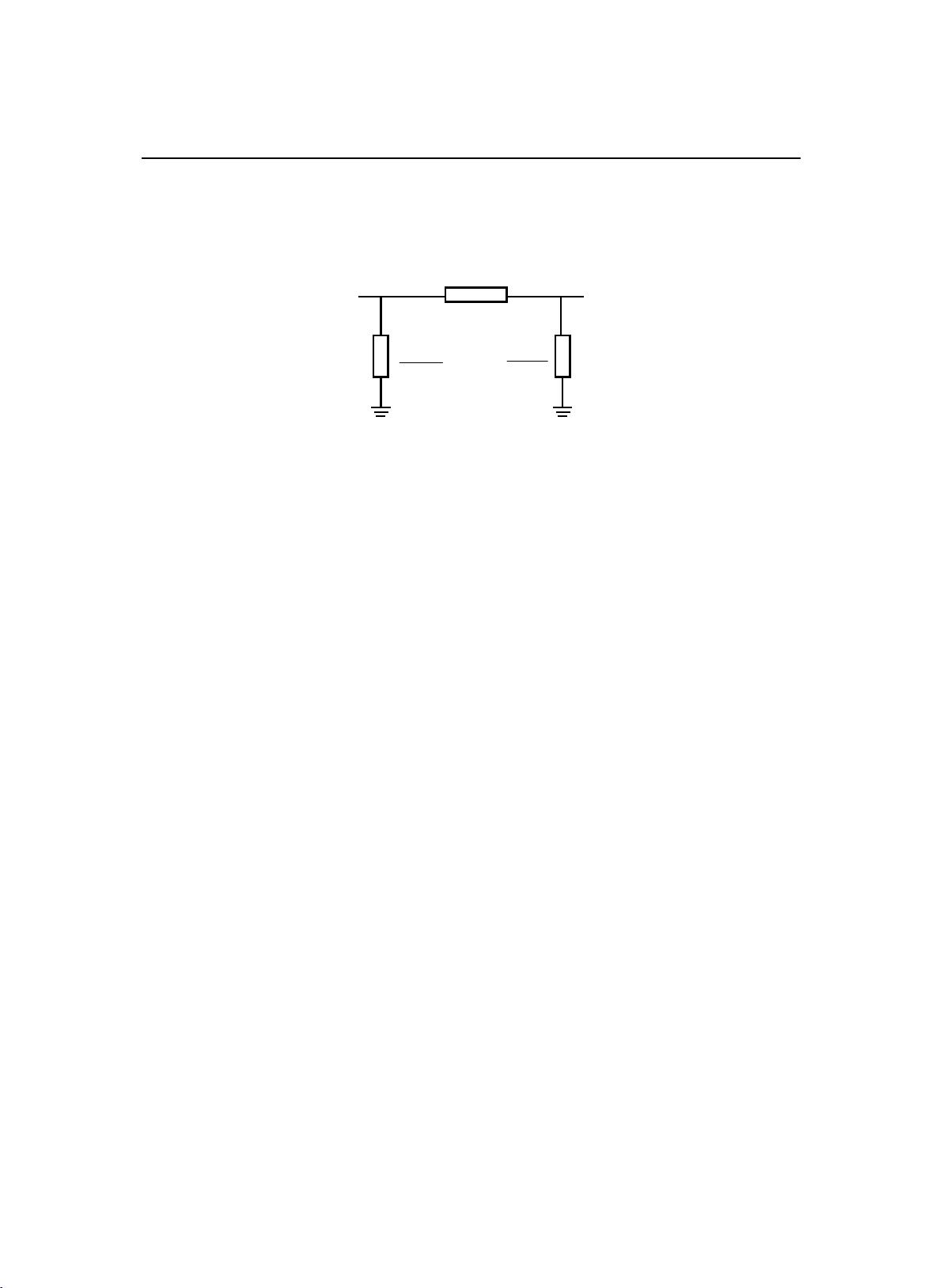
In the realm of power system analysis, flow calculation stands as a fundamental pillar. It is essential not only for the steady-state analysis of the system but also for verifying its functionality. Among the various methods of flow calculation, the PQ decomposition method, also known as the fast decoupled method, has emerged as a significant technique since the 1970s. This method, born out of the Newton R process, has proven to be a valuable tool in power system analysis.
The PQ decomposition method is crucial for simplifying the complex calculations involved in power system analysis. It allows for the decoupling of active and reactive power flows, making the calculations more manageable and efficient. This method has been widely adopted in the industry due to its effectiveness and accuracy in predicting power flow patterns.
One of the key advantages of the PQ decomposition method is its speed. By breaking down the power flow equations into separate active and reactive components, the calculations can be performed more quickly and with less computational effort. This is particularly important in large-scale power systems where real-time monitoring and control are essential.
Another significant benefit of the PQ decomposition method is its versatility. It can be applied to various types of power systems, including radial and meshed networks, making it a valuable tool for power system engineers and researchers. Additionally, the method can be easily integrated with other power system analysis techniques, enhancing its utility and effectiveness.
In conclusion, the PQ decomposition method is a valuable and efficient tool for power system analysis. Its speed, accuracy, and versatility make it an indispensable technique for researchers and engineers in the field. As technology continues to advance, the PQ decomposition method will likely play an increasingly vital role in shaping the future of power system analysis and grid optimization.
2021-07-03 上传
2022-10-27 上传
2024-10-09 上传
2021-10-17 上传
2023-08-19 上传
programxh
- 粉丝: 17
- 资源: 1万+
最新资源
- JHU荣誉单变量微积分课程教案介绍
- Naruto爱好者必备CLI测试应用
- Android应用显示Ignaz-Taschner-Gymnasium取消课程概览
- ASP学生信息档案管理系统毕业设计及完整源码
- Java商城源码解析:酒店管理系统快速开发指南
- 构建可解析文本框:.NET 3.5中实现文本解析与验证
- Java语言打造任天堂红白机模拟器—nes4j解析
- 基于Hadoop和Hive的网络流量分析工具介绍
- Unity实现帝国象棋:从游戏到复刻
- WordPress文档嵌入插件:无需浏览器插件即可上传和显示文档
- Android开源项目精选:优秀项目篇
- 黑色设计商务酷站模板 - 网站构建新选择
- Rollup插件去除JS文件横幅:横扫许可证头
- AngularDart中Hammock服务的使用与REST API集成
- 开源AVR编程器:高效、低成本的微控制器编程解决方案
- Anya Keller 图片组合的开发部署记录