能量梯度理论解析Taylor-Couette流动不稳定性

需积分: 7 123 浏览量更新于2024-09-11 收藏 1.56MB PDF 举报

"文章探讨了由Huashu Dou提出的能量梯度理论在解决Taylor-Couette流动（位于两个同心旋转圆筒之间）不稳定性问题中的应用。该理论在之前的研究所证明适用于壁面约束的平行流，并且确定了对于平行流（包括平面泊肃叶流、管状泊肃叶流和平面科氏流）的湍流转变临界能量梯度参数Kmax约为370-389，在此值以下不会出现湍流。本文详述了计算能量梯度的详细推导过程及其在Taylor-Couette流动不稳定性分析中的应用。" 文章标题“Instability of Taylor–Couette flow between concentric rotating cylinders”关注的是一个经典流体力学问题，即Taylor-Couette流动的不稳定性。这种流动发生在两个同心旋转的圆筒之间，其中内筒和外筒以不同的速度旋转，导致流体在它们之间形成螺旋状的涡旋。这种流动模式在许多工程和自然现象中都有所体现，例如化学反应器、地球大气层和星系形成等。描述中提到的“能量梯度理论”是由Huashu Dou提出的一种新理论，用于研究流动的稳定性。能量梯度理论是一种分析流动状态是否趋向于稳定或不稳定的方法，它着重于能量分布的梯度变化。在之前的研究中，该理论已成功应用于壁面约束的平行流，如平面泊肃叶流（流经平板之间的流体）、管状泊肃叶流（通过管道的流体）和平面科氏流（两个平行板间相对运动的流体）。这些流动的共同特点是存在壁面，流体受到壁面的约束。据描述，对于这些壁面约束的平行流，能量梯度理论确定了一个关键阈值Kmax，当其超过这个值时，流动会从层流向湍流转变。在这个阈值以下，流体保持稳定，没有湍流发生。Kmax的数值大约在370到389之间，这是一个重要的定量指标，有助于预测和控制流体动力学系统中的湍流行为。文章的部分内容提到了详细的推导过程，这可能包括如何计算能量梯度参数以及如何利用这些参数来评估Taylor-Couette流动的不稳定性。通过这样的分析，研究者能够理解在不同旋转速度比和圆筒半径比下，流体何时会从有序的旋转模式转变为混沌的湍流状态。这篇论文通过能量梯度理论为理解和预测Taylor-Couette流动的不稳定性提供了新的视角，这对于优化相关设备设计、控制流体流动和理解自然界的流动现象具有重要意义。此外，这项工作也扩展了能量梯度理论的应用范围，表明该理论不仅可以用于简单的平行流，还能够处理更复杂的同心旋转圆筒之间的复杂流动情况。

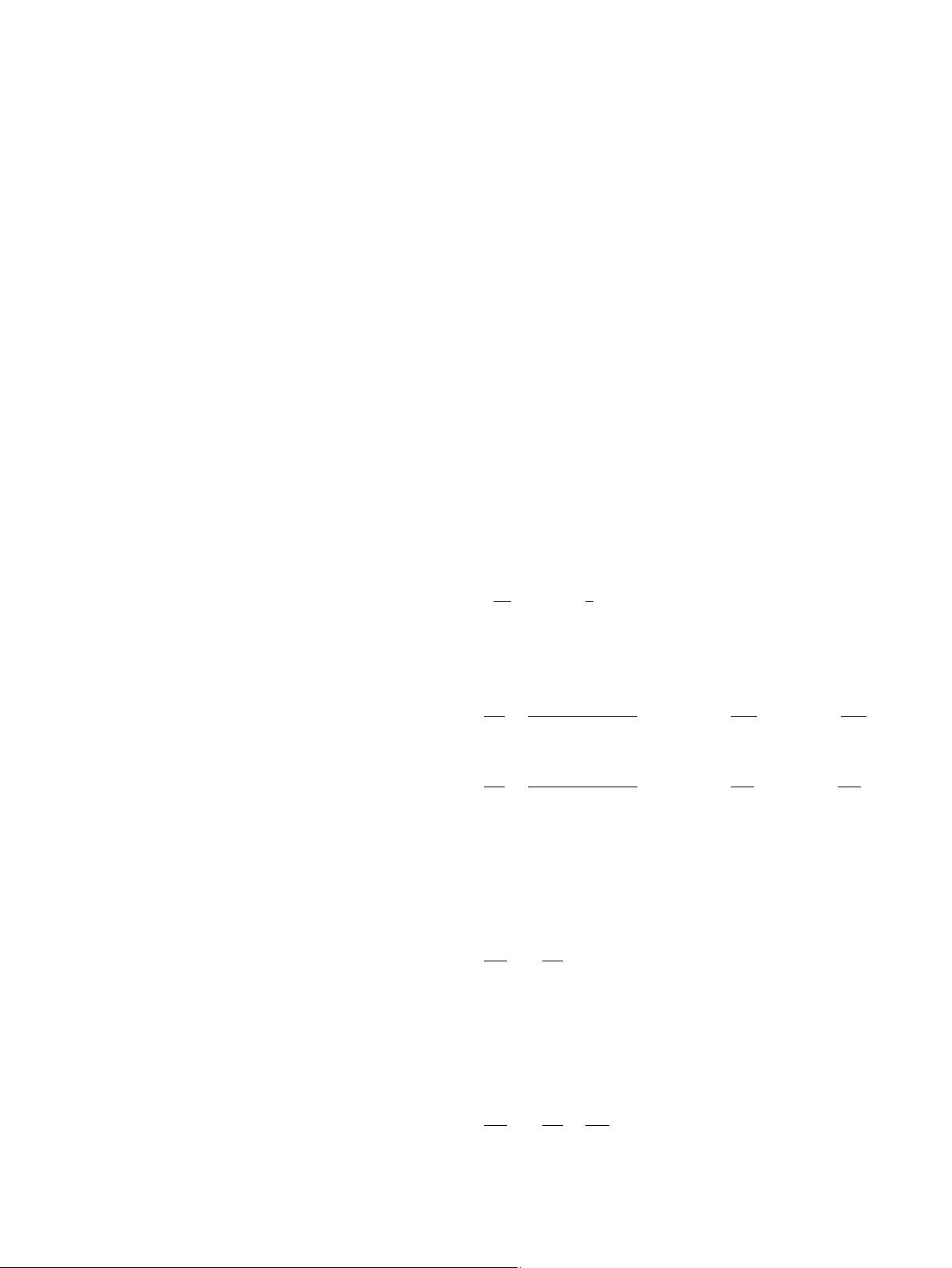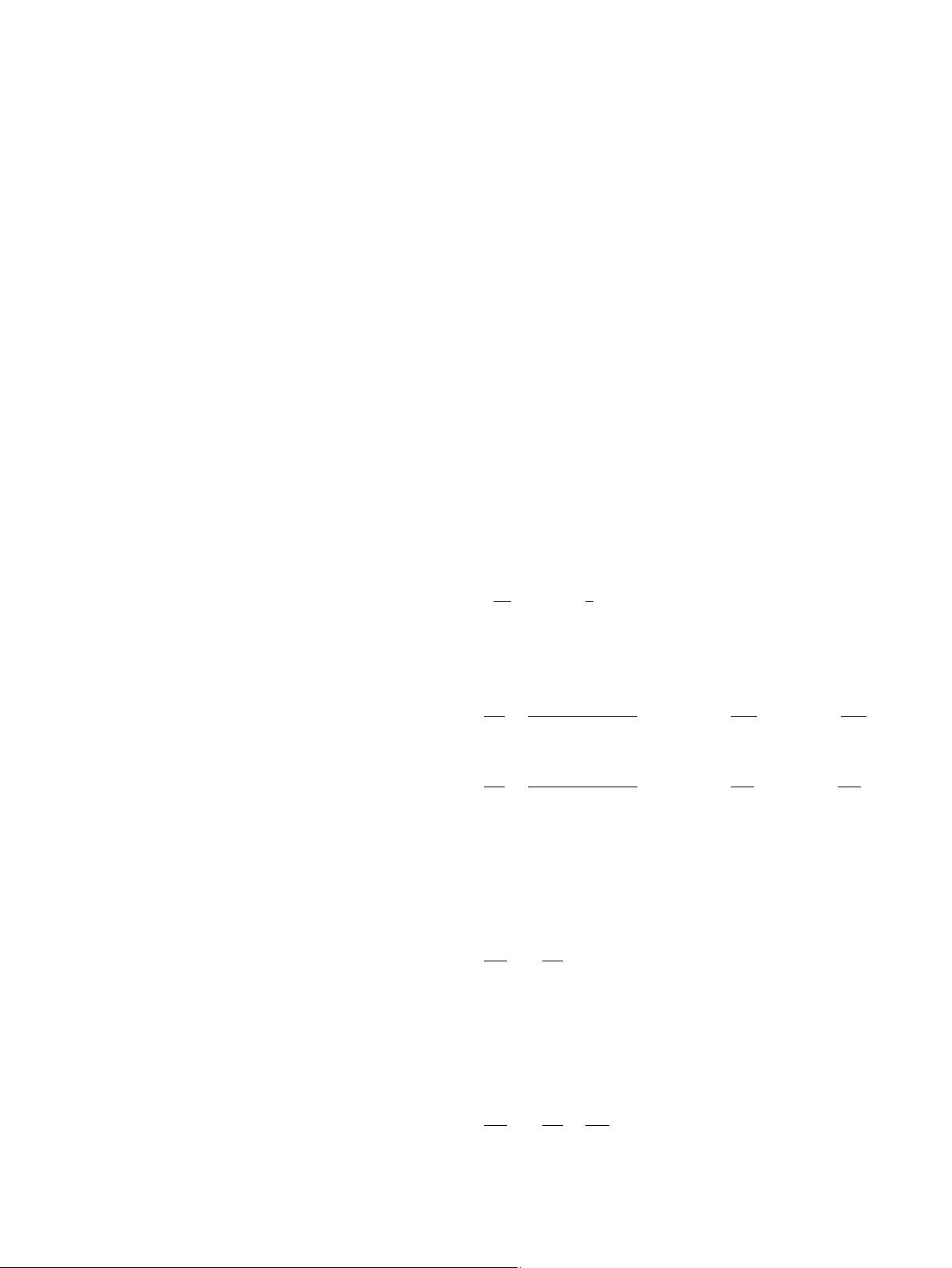
1424 H.-S. Dou et al. / International Journal of Thermal Sciences 47 (2008) 1422–1435

higher Re number and low curvature, the ﬂow may transit to

turbulence earlier and yet does not violate Taylor’s criterion.

Recently, Dou [21,22] proposed a new energy gradient the-

ory to analyze ﬂow instability and turbulent transition prob-

lems. In this theory, the critical condition for ﬂow instability

depends both on the base ﬂow and the disturbance which agrees

with the experimental observations. For a given disturbance, the

critical condition for ﬂow instability and turbulent transition is

determined by the ratio (K ) of the gradient of total mechanical

energy in the transverse direction to the loss of total mechanical

energy in the streamwise direction. For a given ﬂow geome-

try and ﬂuid properties, when the maximum of K in the ﬂow

ﬁeld is larger than a critical value, it is expected that instability

would occur for some initial disturbances provided that the dis-

turbance energy is sufﬁciently large. For plane Poiseuille ﬂow

(channel ﬂow), Hagen–Poiseuille ﬂow (pipe ﬂow), and plane

Couette ﬂow (simple shear ﬂow), the ﬁndings based on the

theory are consistent with the experimental observations; for

the experimental determined critical condition, K

= 370–389

for all the above mentioned three types of ﬂows below which

there is no occurrence of turbulence. In these comparisons, the

distribution of K was calculated for each ﬂow and the value

of K

was obtained using the experimental data at critical con-

dition [21–23]. The theory also suggests the mechanism of

instability associated with an inﬂectional velocity proﬁle for

viscous ﬂows. The theory has been extended to curved ﬂows

with similar derivations to parallel ﬂows and three important

theorems have been obtained [24]. This theory has also been

employed to study the viscoelastic ﬂows where the effect of

elastic force is dominating [25]. It should be mentioned that the

energy gradient theory is a semi-empirical theory since the crit-

ical value of K is observed and determined experimentally and

cannot be directly calculated from the theory so far. In this the-

ory, only the critical condition for the instability is sought after

and the detailed process of instability is not provided.

In this study, we apply the energy gradient theory to analyze

the Taylor–Couette ﬂow between concentric rotating cylinders,

and aim to demonstrate that the mechanism of instability in

Taylor–Couette ﬂow can be explained via the energy gradi-

ent concept. Through comparison with experiments, we show

that the energy gradient function K as a stability criterion is

sufﬁcient to describe and characterize the ﬂow instability in

Taylor–Couette ﬂow. We also show that plane Couette ﬂow can

be considered as just the limiting case of Taylor–Couette ﬂow

when the curvature of the walls tends to zero. For ﬂow between

concentric rotating cylinders, the ﬂow instability may be in-

duced by rotation of the inner cylinder or the outer cylinder.

If it is induced by the former, a Taylor vortex cell pattern will

be formed when the critical condition is violated as in the exper-

iments; if it is induced by the latter, Taylor vortex cell pattern

will not occur and the ﬂow may directly transit to turbulence

when the critical condition due to inertia force is reached as in

plane Couette ﬂow [1–3,6]. In this study, only the critical con-

dition for the former situation is considered/treated.

2. Energy gradient theory revisited

Dou [21] proposed a mechanism with the aim to clarify the

phenomenon of transition from laminar ﬂow to turbulence for

wall-bounded shear ﬂows. In this mechanism, the whole ﬂow

ﬁeld is treated as an energy ﬁeld. It is proposed that the gradi-

ent of total mechanical energy in the transverse direction of the

main ﬂow and the total mechanical energy loss from viscous

friction in the streamwise direction dominate the instability

phenomena and hence the ﬂow transition for a given distur-

bance. It is suggested that the energy gradient in the transverse

direction has the potential to amplify a velocity disturbance,

while the viscous friction loss in the streamwise direction can

resist and absorb this disturbance. The ﬂow instability or the

transition to turbulence depends on the relative magnitude of

these two roles of energy gradient ampliﬁcation and viscous

friction damping of the initial disturbance. In [22], more de-

tailed derivation has been given to exactly describe this mech-

anism, and this theory is termed as “energy gradient theory”.

Here, we give a short discussion for a better understanding of

the work presented in this study.

The equation of total mechanical energy for incompress-

ible ﬂow by neglecting the gravitational energy can be written

as [21],

∂u

∂t

+∇



p +

ρu



= μ∇

u + ρ(u ×∇×u) (1)

For pressure driven ﬂows, the derivatives of the total mechani-

cal energy in the transverse direction and the streamwise direc-

tion can be expressed, respectively, as [21–24],

∂E

∂n

∂(p + (1/2)ρu

)

∂n

= ρ(u × ω) ·

|dn|

+ (μ∇

u) ·

|dn|

= ρuω + (μ∇

(2)

∂E

∂s

∂(p + (1/2)ρu

)

∂s

= ρ(u × ω) ·

|ds|

+ (μ∇

u) ·

|ds|

= (μ∇

(3)

where ω =∇×u is the vorticity. Since there is no work input in

the pressure driven ﬂows, the magnitude of the total mechanical

energy loss of unit volumetric ﬂuid along the streamwise direc-

tion equals to the derivatives of the total mechanical energy in

the streamwise direction, that is

∂H

∂s

=−

∂E

∂s

(4)

For shear driven ﬂows, the derivatives of the total mechan-

ical energy in the transverse direction is the same as Eq. (2).

The energy loss of unit volumetric ﬂuid along the streamwise

direction equals to the derivatives of the total mechanical en-

ergy in the streamwise direction plus the work done to the ﬂuid

by external,

∂H

∂s

=−

∂E

∂s

∂W

∂s

(5)

where W is the work done to the unit volume ﬂuid by external.

For a given base of parallel ﬂow, the ﬂuid particles may move

in an oscillatory pattern in the streamwise direction if they are

剩余13页未读，继续阅读

benanqing123

粉丝: 0

能量梯度理论解析Taylor-Couette流动不稳定性

Strong Instability of Standing Waves for the Nonlinear Klein–Gordon Equation

On the nonlinear instability of fiber suspensions in a Poiseuille flow

On the Instability of Bitcoin Without the Block Reward

The effects of negative ions on the modulational instability of dust acoustic wave with adiabatic dust charge variation

Study of flow instability in a centrifugal fan based on energy gradient theory

The Instability of Spiky Steady States for a Competing Species Model with Cross-Diffusion

Strong Modulation Instability in a Silicon–Organic Hybrid Slot Waveguide

JEDEC JEP184：2021 Guideline for evaluating Bias Temperature Instability of Silicon Carbide Metal-Oxide-Semiconductor Devices for Power Electronic Conversion - 完整英文电子版（44页）.pdf

Dynamic stabilization of plasma instability

Six common Reasons of power Instability

最新资源