LADRC控制器调参原理与应用

需积分: 0 170 浏览量更新于2024-08-05 收藏 154KB PDF 举报

"高志强老师对LADRC(Linear Active Disturbance Rejection Control，线性主动干扰抑制控制)的推导原理" 这篇资料主要由高志强老师讲解了LADRC控制器的设计与调参方法，其核心是针对2003年美国自动控制学会(ACC)会议上提出的一种新型控制策略。LADRC是一种融合了经典PID控制和鲁棒控制思想的先进控制技术，旨在有效抑制系统中的不确定性和外部干扰。 1. 控制器缩放(Ctrl Scaling)：控制器缩放是将已有的控制器设计通过频率尺度变换，使其适用于一大类增益和带宽不同的被控对象。这个过程消除了针对不同植物模型重复进行控制器调参的需求，提高了设计效率。 2. 控制器参数化(Ctrl Parameterization)：通过将控制器参数设定为一个单一变量——环路增益带宽的函数，控制器参数化大大简化了调参过程。这意味着，只需调整一个参数（带宽），就能影响整个控制器的行为，降低了调参的复杂度。 3. 实际优化(Practical Optimization)：实际优化定义为在满足物理限制条件的前提下最大化带宽，这是决定系统性能的临界因素。这一步骤确保了控制器在提升系统响应速度的同时，不会超出系统本身的运行边界。 4. 关键词：文档涵盖了调参、PID控制、控制器缩放、自动缩放、自动调参、自适应自调谐、增益调度、扰动观测器和计算机辅助控制器设计等多个关键词，展示了LADRC在控制科学领域的应用和发展。 5. 引言：引言部分强调了控制器调参的重要性，指出比例-积分-微分(PID)控制作为最常用的方法，虽然简单易用，但在面对非线性、时变或存在不确定性的情况时往往力不从心。LADRC的出现，结合了PID的实用性与现代控制理论的稳健性，为解决这些问题提供了新的解决方案。这篇资料深入探讨了LADRC控制器的原理及其调参工具，为控制系统设计者提供了一套科学且实用的方法，有助于提升系统的性能和鲁棒性。

Scaling and Bandwidth-Parameterization Based

Controller Tuning

Zhiqiang Gao

Dept. of Electrical and Computer Engineering

Cleveland State University, Cleveland, Ohio 44115

Abstract: A new set of tools, including controller scaling,

controller parameterization and practical optimization, is

presented to standardize controller tuning. Controller scaling is

used to frequency-scale an existing controller for a large class of

plants, eliminating the repetitive controller tuning process for

plants that differ mainly in gain and bandwidth. Controller

parameterization makes the controller parameters a function of a

single variable, the loop-gain bandwidth, and greatly simplifies

the tuning process. Practical optimization is defined by

maximizing the bandwidth subject to the physical constraints,

which determine the limiting factors in performance.

Collectively, these new tools move controller tuning in the

direction of science.

Keywords: Tuning, PID, Scaling, Auto-Scaling, Auto-Tuning,

Adaptive Self-Tuning, Gain-Scheduling, Disturbance Observer,

Computer Aided Controller Design

Introduction

The proportional-integral-derivative (PID) controller, first

proposed by N. Minorsky in 1922 [1], is used in over 90% of

current industrial control applications [2]. In addition, the

controller parameters are still determined by rules of thumb, such

as look-up tables [3].

Classical control theory has successfully provided the analysis

and design tools for single-input single-output (SISO), linear,

time-invariant systems, since the 1940s. The PID design

approach moved from empirical (i.e., ad hoc tuning methods such

as Ziegler and Nichols tuning tables [3]) to analytical (i.e., pole

placement, frequency response). In particular, the frequency

response-based methods (Bode and Nyquist plots, stability

margins, lead-lag compensators) have proved to be especially

useful in solving control problems.

Historically, determining controller parameters to meet design

specifications (tuning

), rather than the design of the controller

itself, has been the main concern in industry. Most industrial

plants are inherently stable and consist of SISO subsystems.

Simple PID controllers implemented in a digital form can usually

meet the performance needs. But the problem of tuning has

hardly received much attention in the existing control theory. The

variety of ad-hoc tuning algorithms in industrial control products

shows the lack of in-depth understanding of the problem and the

need for further research.

The PID gains are commonly “tuned” on a trial-and-error basis in

practice. A general lack of knowledge regarding the relationship

between “design objectives” and “practical performance

measures” makes the use of well-known design techniques such

as Root Locus (pole-placement) and linear optimal control

difficult. For example, in pole-placement design, the objective is

to place the closed-loop poles at given locations, based on the

understanding of how the location of poles affects the transient

response of a system. Although the transient response is usually

an important design consideration, it is not the only issue in pole-

placement methods with which to contend. The pole-placement

method is ill-equipped to handle other common design

specifications including disturbance rejection, noise sensitivity,

stability margins, and smoothness of the control signal.

This lack of design insight leads to the heuristic nature of the

tuning methods implemented in industry. Furthermore, the

practice of control design and tuning tended in the direction of art

rather than science. This paper presents a comprehensive

approach that moves control design and tuning in the direction of

science.

The paper is organized as follows. Controller scaling is

introduced in Section II. Parameterization and optimization of

model-based controllers are discussed in Section III. Design,

parameterization, and optimization of a model-independent

controller design method are discussed in Section IV. Finally,

some concluding remarks are given in Section V.

II. Controller Scaling

A controller is generally not “portable”, i.e., a controller designed

for one plant is usually not applicable to another plant. The

objective of controller scaling is to make a good controller

“portable”, much like the filter design. With the bandwidth, pass

band, and stop band requirements given, the filter design is

straightforward. First, a unit bandwidth filter, such as an nth

order Chebeshev filter H(s), is found that meets the pass band and

stop band specifications; then it is frequency scaled by ω

achieve the desired bandwidth of ω

. It is shown in this section

that the controller design can be performed similarly.

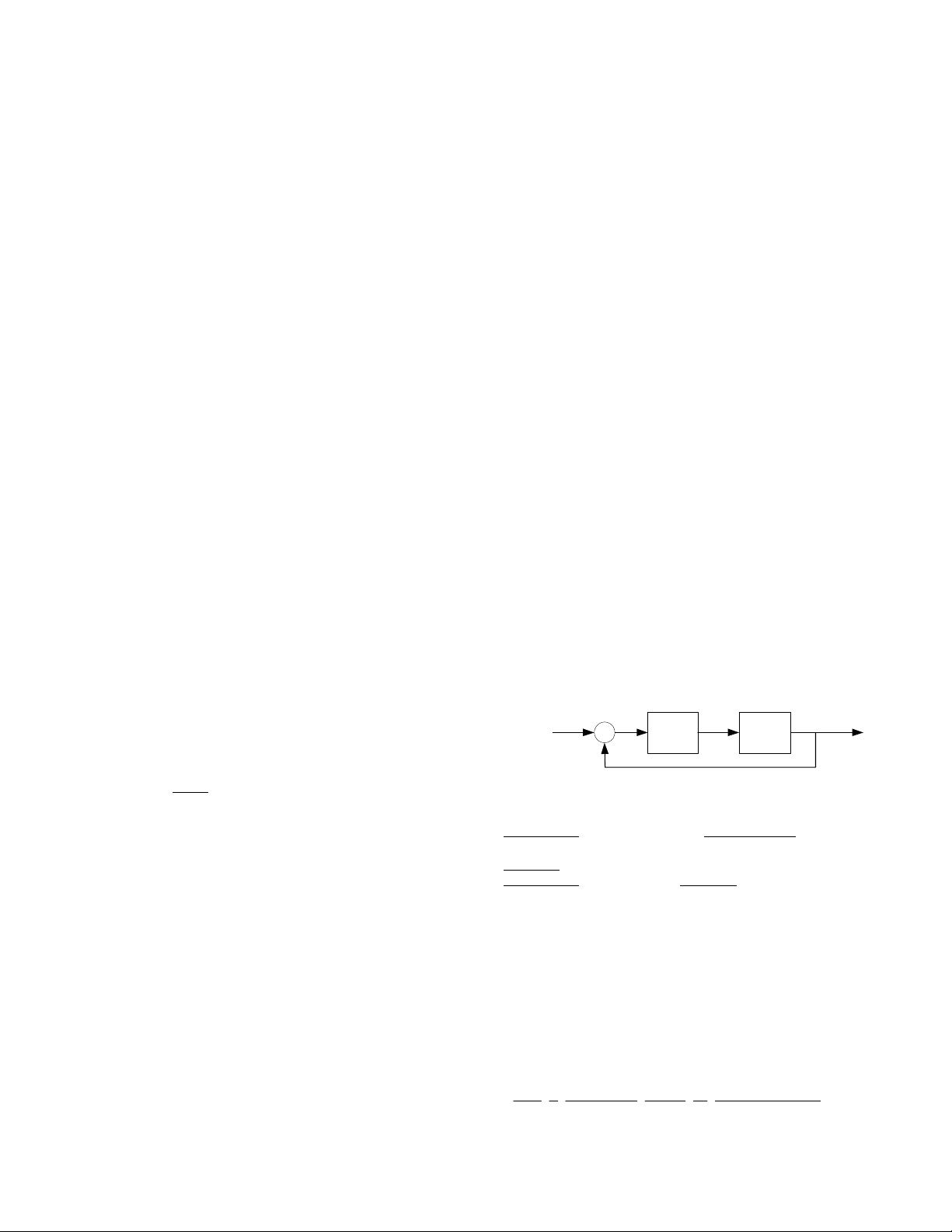
2.1 Frequency Scale and Time Scale

Consider a unit feedback control system with the plant G

(s) and

the controller G

(s), as shown in Figure 2.1. Assume that G

(s)

was designed for desired command following, disturbance and

noise rejection, and stability robustness. Now, consider a similar

class of plants G

(s/ω

), for any given

. Can a controller be

found without a repetition of the tedious loop shaping design

process?

(s)

reference

input

output

Figure 2.1 Feedback Control Configuration

Definition2.1

: Denote

as the frequency scale of the plant

(s/

) with respect to G

(s), and

=1/

, the corresponding

time scale

Definition2.2

: Denote k as the gain scale of the plant kG

(s) with

respect to G

(s).

The differences in many industrial control problems can be

described in terms of the frequency and gain scales defined here,

such as the temperature processes with different time constants (in

first-order transfer functions), motion control problems with

different inertias, motor sizes and frictions.

The use of the scales allows the development of a generic solution

for a class of problems. Any linear time-invariant plant, strictly

proper and without a finite zero, can be reduced to one of the

following forms

2232

11 1 1 1 1

, , , , , , ...

121s(s+1)s 1sss s ss s

ξξξ

+++ +++

(2.1)

Proceedings of the American Control Conference

Denver, Colorado June 4-6, 2003

下载后可阅读完整内容，剩余7页未读，立即下载

文润观书

粉丝: 31
资源: 316

LADRC控制器调参原理与应用

线性自抗扰控制参数b0辨识及参数整定规律 (2015年)

LADRC的matlab和simulink仿真 针对高志强的2003 ACC-LADRC中论文三个例子的Simulink仿真

LADRC.rar_LADRC_LADRC matlab程序_ladrc算法_线性自抗扰_自抗扰

matlab量子力学

ladrc代码，待验证

线性自抗扰控制（LADRC）.zip

LADRC的Simulink仿真

基于LADRC的无人机高精度定高控制

LADRC_matlab_自抗扰_

高志强论文

最新资源

LADRC的matlab和simulink仿真针对高志强的2003 ACC-LADRC中论文三个例子的Simulink仿真