MATLAB实现数字信号处理：三角脉冲、单位脉冲、阶跃序列与频谱计算

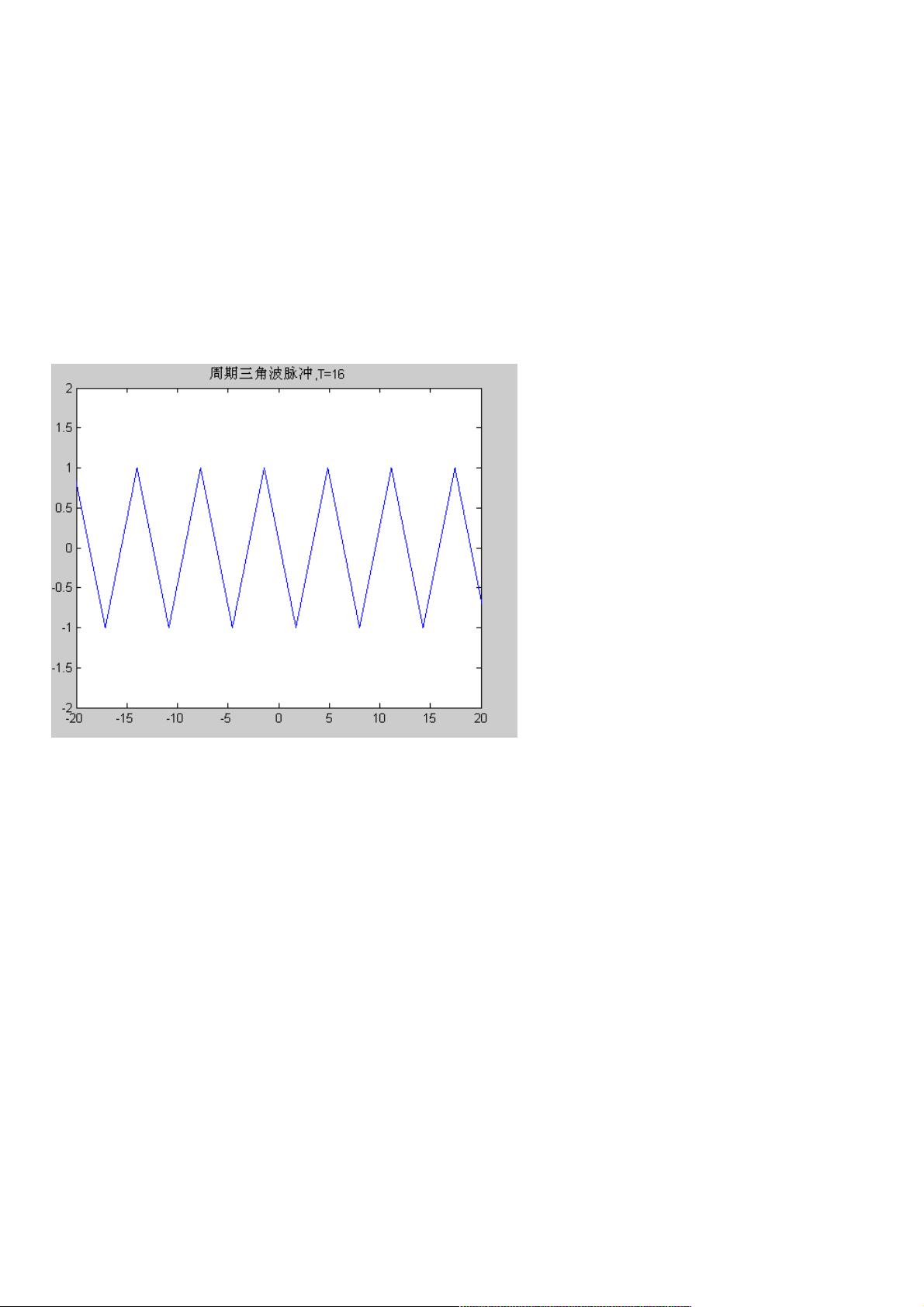
"该资源主要涉及数字信号处理的基本设计，包括使用MatLab生成不同类型的数字信号，如周期为4的三角脉冲波、单位脉冲序列、阶跃序列，以及利用离散傅里叶变换（DFT）计算复指数信号的频谱。此外，还提到了对连续时间信号的时域分析方法的理论探讨。" 在数字信号处理中，基本设计涉及到创建和分析各种信号以理解其特性。以下是对各部分的详细说明： 1.1 **三角脉冲波的生成**：通过MatLab中的`sawtooth`函数可以产生周期性三角波。在这个例子中，T=16，t是时间数组，且t的范围从-2.5T到2.5T，步长为0.01。函数`sawtooth(t-2*T/4,0.5)`产生了一个偏移的三角波，其中第二个参数0.5代表波形的 duty cycle，即波形在一个周期内的高电平时间占比。 1.2 **单位脉冲序列**：单位脉冲序列是一个在时间上具有单一非零值的信号，通常用在信号处理中作为基础元素。MatLab中可以使用`zeros`函数初始化一个全零向量，然后将第一个元素设置为1来生成单位脉冲。后续代码计算了该序列的傅里叶变换，显示了幅度谱和相位谱，这对于理解信号的频率成分至关重要。 1.3 **阶跃序列**：阶跃序列是突然改变的信号，通常用于模拟开关或阈值效应。在MatLab中，通过`sign`函数可以很容易地创建阶跃序列。示例展示了如何生成一个在t=0时刻发生阶跃变化的序列。 1.4 **用DFT计算频谱**：离散傅里叶变换（DFT）是数字信号处理中的核心工具，用于将时域信号转换为频域表示，从而揭示信号的频率成分。这里计算的是两个不同频率的余弦信号的和的频谱。使用`fft`函数进行DFT，`fftshift`确保频谱中心对齐，然后通过`stem`函数绘制出幅度谱和相位谱。 设计理论分析方法部分提到了连续时间信号的时域分析，这是信号处理的基础。时域分析侧重于观察信号随时间的变化，可以直观地理解信号的瞬态行为和周期性特征。然而，对于许多应用，频域分析更有利于识别信号的频率成分，特别是在滤波、调制和解调等场景。 这个资源提供了数字信号处理的基本操作实例，对于学习和理解数字信号处理概念，以及掌握MatLab在该领域的应用非常有帮助。