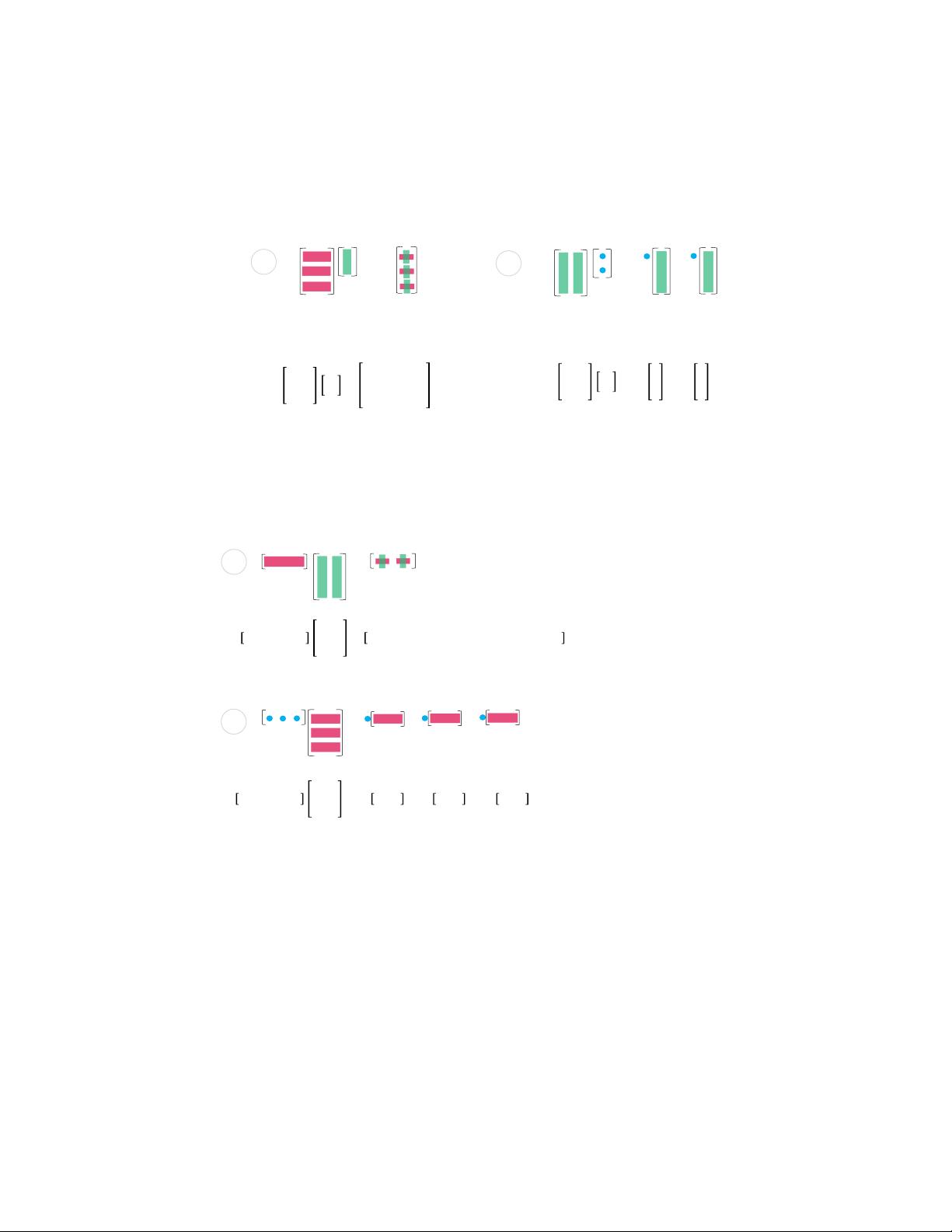
线性代数可视化：矩阵概念与运算图解

"线性代数可视化.pdf 是一本由 Kenji Hiranabe 创作的图形笔记，旨在通过可视化方式帮助读者理解 Gilbert Strang 在《Linear Algebra for Everyone》一书中介绍的线性代数核心概念，特别是矩阵分解。这本书包含了矩阵乘法、向量和矩阵的视觉表示、以及多种矩阵分解方法，如 Column-Row (CR) 分解、Gaussian Elimination (LU 分解)、Gram-Schmidt 正交化 (QR 分解)、特征值与对角化 (Eigenvalues and Diagonalization, QΛQT) 和奇异值分解 (Singular Value Decomposition, UΣVT)。书中的插图和解释旨在促进对线性组合、秩1矩阵和线性代数艺术的理解。" 线性代数是数学的一个基础分支，特别是在计算机科学和工程领域中具有广泛的应用。这本书首先介绍了理解矩阵的不同视角，包括从几何和代数的角度来看向量乘以向量、矩阵乘以向量以及矩阵乘以矩阵。矩阵乘法不仅是简单的点积操作，更代表了线性变换，能够将一个空间转换到另一个空间。 接着，书中详细探讨了五种重要的矩阵分解方法： 1. **Column-Row (CR) 分解**：这是一种将矩阵分解为列向量和行向量乘积的形式，有助于理解矩阵的结构和其作用于向量的方式。 2. **Gaussian Elimination (LU 分解)**：通过一系列行变换，将矩阵转化为上三角矩阵（U）和下三角矩阵（L）的乘积，这在求解线性方程组时非常有用。 3. **Gram-Schmidt 正交化 (QR 分解)**：将任意矩阵转化为正交矩阵（Q）与上三角矩阵（R）的乘积，常用于数据降维和数值计算。 4. **特征值与对角化 (Eigenvalues and Diagonalization, QΛQT)**：矩阵可以被分解为一个正交矩阵 Q、一个包含特征值的对角矩阵 Λ 以及 Q 的转置 QT 的乘积，这一过程揭示了矩阵在特定向量空间上的本质性质。 5. **奇异值分解 (SVD, UΣVT)**：将任何矩阵分解为两个酉矩阵（U 和 V）和一个对角矩阵（Σ）的乘积，其中对角线上的元素是奇异值，SVD 在信号处理、图像压缩和数据分析等领域有着广泛应用。 这些分解方法不仅有助于理解矩阵的内在特性，而且在数值计算、优化问题、统计分析和机器学习等实际问题中扮演着关键角色。通过 Kenji Hiranabe 的可视化方法，读者可以更直观地掌握这些概念，提高学习效率。这本书对于初学者和有一定经验的学习者都是宝贵的资源，尤其是那些希望通过视觉辅助加深对线性代数理解的人。