IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS, VOL. 6, 2007 553
Joint SVD of Two Cross-Correlation Matrices
to Achieve Automatic Pairing in 2-D
Angle Estimation Problems
Jian-Feng Gu and Ping Wei, Member, IEEE
Abstract—Recently, Kikuchi et al. proposed a pair-matching
method for two-dimensional (2-D) angle estimation using a
cross-correlation matrix. Unlike some classical pair matching
methods which require a complex process, Kikuchi’s Method uti-
lizes the corresponding combinations of the elevation and azimuth
angles emerging in the cross-correlation matrix of two uniform
linear arrays (ULAs) to achieve automatic pairing. However,
Kikuchi’s method has some drawbacks such as the pair matching
and failure problems when the difference of the corresponding
combinations of the 2-D angles
cos cos
=1
is small
and the signal-to-noise ratio (SNR) is low. Furthermore, this
method does not make good use of the cross correlation, where
the effect of additive noise is eliminated, to improve the estimation
performance. We propose a novel automatic pairing scheme for es-
timating 2-D angle by simultaneous singular value decomposition
(SVD) of two cross-correlation matrices. Computer simulation
results are presented to show that the proposed technique can
overcome these problems and offer better estimation performance.
Index Terms—Automatic pairing, cross-correlation matrix, joint
SVD, two-dimensional (2-D) angle.
I. INTRODUCTION
T
HE two-dimensional (2-D) direction-of-arrival (DOA)
estimation using a 2-D array of sensors has received
considerable attention in the recent array signal processing
literature. Much research has been done based on the uniform
rectangular array (URA) [1]–[3] because the URA can be re-
garded as the 2-D extension of the uniform linear array (ULA).
However, these methods need a number of sensors to achieve
high resolution and give accurate estimates. It has been proven
in [4] that the L-shaped array has better estimation performance
than many other simple structured arrays. More recently,
there has been growing interest in developing 2-D angles
estimators by exploiting the L-shaped arrays [5]–[7]. Tayem
and Kwon [6] presented a computationally simple 2-D DOA
estimation with propagator method using one or two L-shaped
arrays. However, this method may cause the pair matching
and failure problems [7]. Consequently, Kikuchi
et al. [7]
proposed a pair-matching method to remove the aforesaid
problems using a cross-correlation matrix. The Kikuchi’s
method still has several drawbacks: 1) it will cause the pair
matching problems when the difference of the corresponding
Manuscript received December 5, 2006; revised August 21, 2007.
The authors are with the Department of Electronic Engineering, University of
Electronic Science and Technology of China, Chengdu, Sichuan 610054, China
(e-mail: Gujianfeng@uestc.edu.cn; Pwei@uestc.edu.cn).
Digital Object Identifier 10.1109/LAWP.2007.907913
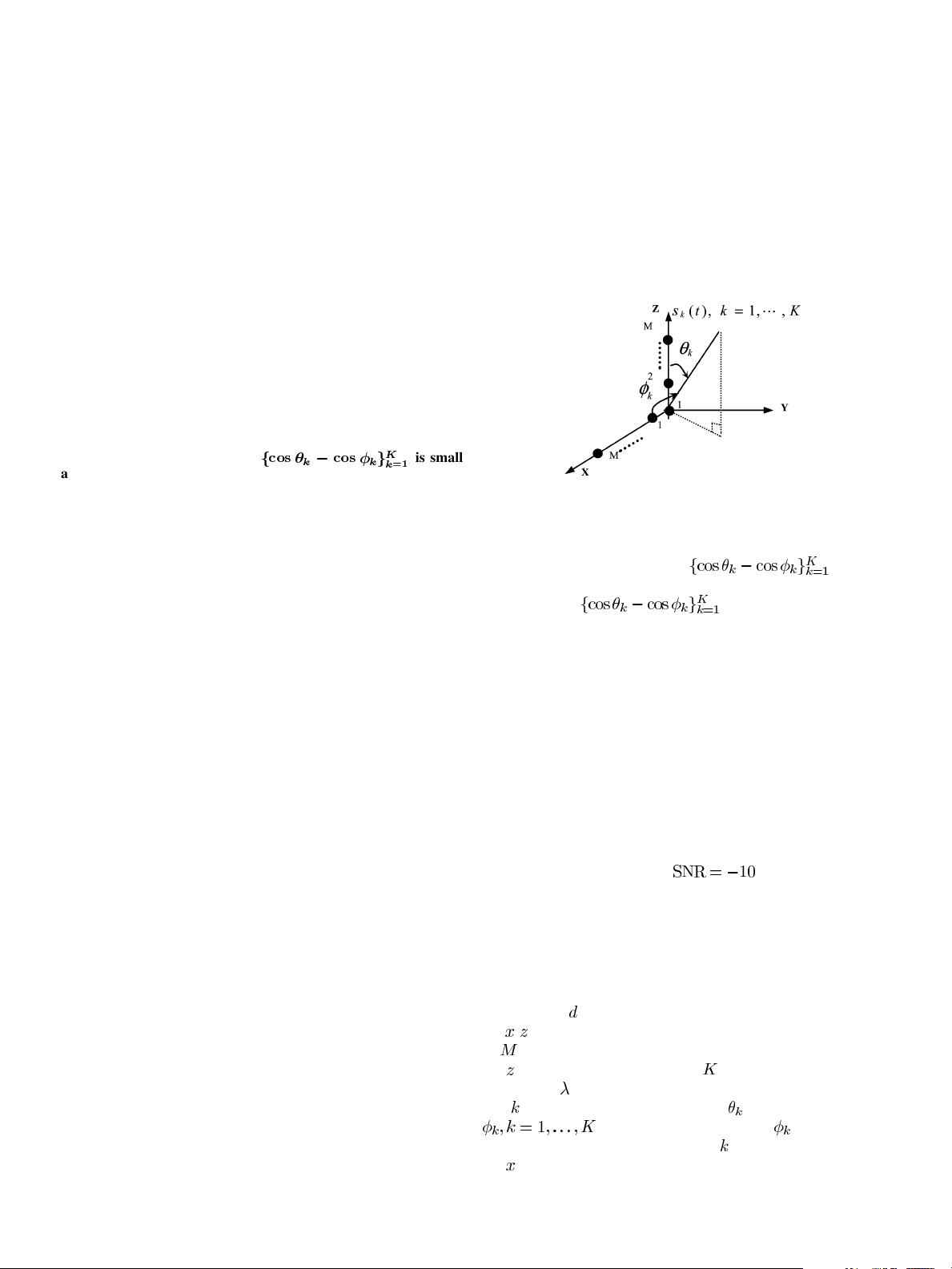
Fig. 1. Array elements configuration for the joint elevation and azimuth DOA
estimation [7].
combinations of the 2-D angles is small
and the signal-to-noise ratio (SNR) is low. This is mainly due
to the fact that
is still estimated by con-
ventional DOA techniques [7]. 2) It encounters an estimation
failure problem when the angular separation of the azimuth
angles is small. 3) It does not make good use of the cross
correlation, where the effect of additive noise is eliminated
[8], to improve the estimation performance. Therefore, the
objectives of this letter are: 1) to remove those problems in
the Kikuchi’s method; and 2) to further improve the perfor-
mance of the Kikuchi’s method. To achieve these objectives,
we present a new automatic pairing technique for 2-D DOA
estimation by joint singular value decomposition (SVD) of two
cross-correlation matrices, where the effect of additive noise is
eliminated. Computer simulations show that the proposed tech-
nique can overcome these problems and offer better estimation
performance. For example, at
dB, our method can
obtain almost 80% detection rate of successful pair matching
while the cross-correlation matrix method based on ESPRIT
(CCM-ESPRIT) can only reach 20% [7].
II. D
ATA MODEL
Consider two uniform linear orthogonal arrays with interele-
ment spacing
, making up of the L-shape array configuration in
the
- plane as shown in Fig. 1, [7]. Each linear array consists
of
elements and the element placed at the origin belongs to
the
axis. Suppose that there are narrowband sources with
wavelength
impinging on the array from distinct directions.
The
th source has an elevation angle and an azimuth angle
. Note that the definition of is the same as
Fig. 2 of the [7], i.e., the angle of the
th source with respect to
the
axis as shown in Fig. 1. These sources are assumed to be
in the far field with respect to the sensor location. The observed
1536-1225/$25.00 © 2007 IEEE









