群目标结构建模与多伯努利滤波估计：图论方法

62 浏览量更新于2024-07-14 收藏 1.36MB PDF 举报

本文主要探讨了在杂乱环境下的多可分辨群目标估计问题，利用图论和多伯努利滤波器进行结构建模和估计。作者们关注的是在复杂背景下，如何有效地处理目标群体的信息，并准确估计群体的各个个体状态以及群体整体特性。首先，论文提出了一种动态模型和观测函数，针对群目标的运动和测量特性进行了系统化建模。动态模型考虑了群内目标之间的依赖关系，包括它们的位置、速度、方向等随时间变化的状态。而观测函数则定义了在杂乱背景中，传感器如何从观测数据中提取群目标的信息，如反射回波信号。其次，通过预测的目标状态，作者们进一步挖掘了群内个体目标之间的关联性。这种连接关系对于理解和推断群体行为至关重要，因为它允许算法在估计单个目标的同时，也能够估计整个群体的状态，如群体大小和形状等关键特征。这一步骤利用了图论的工具，将目标间的相互作用视为网络中的节点和边，从而构建出一个表示目标间依赖关系的图模型。接着，作者们引入了多伯努利滤波器，这是一种适用于处理随机有限集合的估计方法，特别适合于处理具有不确定性和噪声的估计问题。通过多伯努利滤波器，可以迭代地更新每个目标的状态概率分布，同时考虑到它们之间的相互影响，从而得到更精确和鲁棒的估计结果。文章历史部分显示，该研究经历了从最初的提交到多次修订的过程，直到2017年11月获得接受，这表明作者们对方法的深入研究和不断完善。关键词"可分辨群目标"、"依赖关系"、"随机有限集"、"图论"和"多伯努利滤波器"都突出了本文的核心内容和研究重点。总结来说，这篇研究论文提供了一种有效的方法，通过结合图论和多伯努利滤波器技术，解决在杂乱环境中对多可分辨群目标的实时估计问题，为群体目标跟踪、监测和理解提供了重要的理论支持和技术手段。这种方法对于军事、航天、交通等领域，特别是在高密度目标环境下的应用具有实际价值。

W. Liu et al. / Automatica 89 (2018) 274–289 277

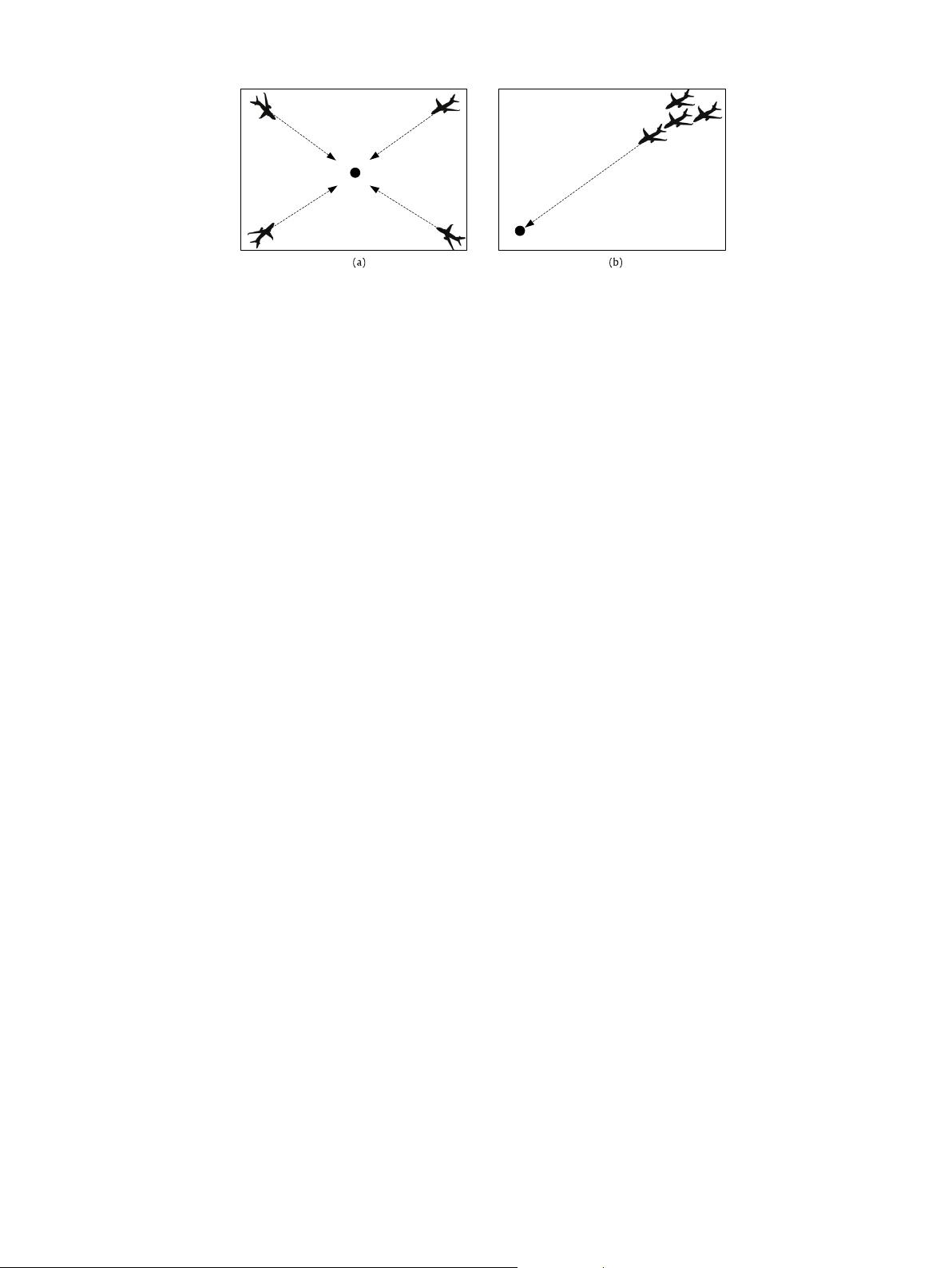
Fig. 1. The group is in collaboration. (a) Four targets of a group move to a collective point from four positions; (b) Four targets of group forming a formation move to a point.

Throughout this paper, we assume that graph G

is a simple graph

and has no loops. According to whether each edge has an assigned

orientation, a graph can be classified into the undirected graph and

directed graph (digraph), respectively.

A digraph is a graph in which the edges have direction. This

is usually indicated with an arrow on the edge; more formally, if

k,i

and v

k,j

are vertices, an edge is an unordered pair {v

k,i

, v

k,j

while a directed edge, called an arc, is an ordered pair (v

k,i

, v

k,j

) or

k,j

, v

k,i

). The arc (v

k,i

, v

k,j

) is drawn as an arrow from v

k,i

to v

k,j

(Guichard, 2014).

Definition 1. Two vertices v

k,i

and v

k,j

of a graph G

are said to be

connected if there is a path (v

k,i

, v

k,j

) in G

We further refer the following definition of a tree (Guichard,

2014):

Definition 2. A connected graph G

is a tree if it is a acyclic, that is,

it has no cycles. More generally, an acyclic graph is a forest.

In essential, from the viewpoint of graph theory, each group is

like a tree in the forest (all groups). Whether undirected graph or

digraph can be expressed by an adjacency matrix A(V

) defined by

A : V

× V

→ {0, 1}, where 0 denotes that the any two vertices

are not adjacent, otherwise adjacent. Therefore, the adjacency

matrix for undirected matrix is symmetric, while digraph often

asymmetric.

3. Dynamic models for group targets

3.1. Dependent relation for group targets

Different from common multi-target tracking, the group target

tracking focus on the group state, group dependent relation and

number of subgroups. A primary issue is to judge whether multiple

targets belong to group targets. That is to say, what are the group

targets indeed? In our idea, the group targets are the multiple

targets which move in certain mode of collaboration.

The term collaboration here has a very broad meaning. For

examples, sub-figure (a) of Fig. 1 shows that four targets take off

from several sites and fly to a default point at the same time.

Although the four targets have not a fixed formation and shape,

they are collaboration in the space and time and constitute a group.

Another scenario is shown in sub-figure (b), where four targets

keep a formation and thus are looked as group targets. In this paper,

we mainly focus on the second case of multiple formations which

remain fixed structure as sub-figure (b) of Fig. 1. Hence, we first

propose the following definition for group targets.

Definition 3. Group targets are a set of state points and the state

points move in state space in certain mode of collaboration.

In this definition, the key is the movement of collaboration.

Here, the collaboration denotes there are some kinds of dependent

relation between the targets. The group targets may involve multi-

ple subgroups and in each subgroup the targets are dependent and

form a connected graph. In special case, if the numbers of targets

in each subgroup reduces to one, the group targets will reduce to

the normal case of multiple targets.

Graph theory provides a powerful tool in modeling the de-

pendence between vertices and it has been successfully used in

formation control of flying vehicles (Anderson, Yu, & Fidan, 2006;

Yu, Hendrickx, Fidan, Anderson, & Blondel, 2007) and multi-agent

system control (Ferber, 1999). Inspired by the success, we combine

the graph theory with group targets and define the group targets

with graph structure G

as follows:

Definition 4. Given group targets with fixed number of targets

= {x

k,1

, . . . , x

k,N

} at time step k, the group targets with digraph

structure G

= (V

, E

), where vertex set V

is given by X

, i.e., V

≜

. The edge set E

is defined by the dependent relation between

the vertex set E

≜ X

× X

Remark 1. The structure of group targets can be seen as a kinds of

digraph. Specifically, according to their dependent relation, some

vertices (targets) are parents and some are children. Besides, the

group targets X

may involve multiple subgroups with different

structures. We analyze the structures of individual subgroups on

graph G

3.2. Group target dynamic models

Consider the following linear models for a target x

k,i

in group X

with digraph structure G

given by:

k+1,i



l∈P(i)

(l, i)[F

k,l

+ b

(l, i)] + B

k,i

(17)

k+1,i

= H

k+1

k+1,i

+ v

k+1,i

(18)

k,i

∈ X



l∈P(i)

(l, i) = 1, ω

(l, i) ∈ [0, 1] (19)

where w

k,i

∼ N (0, Q

k,i

), Q

k,i

is covariance matrix of process noise,

(l, i) is a standard (or required) displacement vector between

vertex i and its father vertex l, P(i) is a vertex set and denotes all the

father vertices for vertex i. If P(i) is a empty set ∅, let P (i), b

(l, i)

be i and zero, respectively. For simplicity, the weighted coefficients

{ω

(l, i), l ∈ P(i)} imply a convex combination of various vectors

k,l

, l ∈ P(i)}. In short, the target i is dependent on the states of

its parents.

Besides, different from the usual multi-target dynamic models,

which is shown by Eq. (20), Eq. (17) has nothing to do with its

剩余15页未读，继续阅读

weixin_38732425

粉丝: 6
资源: 942

群目标结构建模与多伯努利滤波估计：图论方法

几种用于多目标滤波的非线性多伯努利滤波器的性能比较

基于标签多伯努利滤波器的多目标跟踪方法

多路径广义标记多伯努利滤波器

幅度信息辅助鲁棒多伯努利滤波器用于海洋目标跟踪

联合概率超图匹配标记多伯努利滤波器的刚性目标跟踪

邻细胞振幅信息的δ广义标记多伯努利滤波器

标签多伯努利滤波器：精确多目标跟踪与身份估计

非线性多伯努利滤波器在多目标跟踪中的性能对比分析

多伯努利滤波器提升过采样点目标检测与跟踪性能

改进的多伯努利滤波器：雷达多目标跟踪中的未知杂波率处理

最新资源