SDM：解决计算机视觉问题的高效稳定方法
5星 · 超过95%的资源 需积分: 10 139 浏览量
更新于2024-09-10
收藏 1.92MB PDF 举报 Supervised Descent Method (SDM) 是一种针对计算机视觉问题，特别是人脸对齐问题的有效算法，它在当前应用广泛且以其高速度和稳定性而著称。该方法由 Xuehan Xiong 和 Fernando Dela Torre 在 Carnegie Mellon University 的 Robotics Institute 发表。SDM的核心理念是解决非线性最小二乘（Non-linear Least Squares, NLS）函数优化中的挑战。
传统的非线性优化方法，如基于梯度的2nd-order descent methods，通常被认为是处理一般光滑函数的高效工具，但它们在计算机视觉领域存在两个主要缺点。首先，由于图像处理任务往往涉及的是非线性和非光滑函数，解析求导可能不可行，这就需要依赖数值近似，这在实际应用中可能效率低下或不精确。其次，Hessian矩阵在很多情况下可能非常大且不是正定的，这会影响优化过程的稳定性和收敛速度。
SDM正是为了克服这些挑战而设计的。在训练阶段，SDM学习并积累一组在不同数据点上最小化NLS函数值的梯度方向序列。这个过程使得SDM能够“学习”如何有效地移动，即使面对非解析函数和复杂约束。在测试阶段，SDM利用学到的梯度方向序列来逐步逼近NLS目标函数的最小值，避免了直接使用数值微分或处理大型Hessian矩阵的困难。
SDM的优势在于其灵活性和适应性，它能够处理复杂的计算机视觉问题，如相机校准、图像对齐和结构从运动（Structure from Motion, SfM）等，而且在实际应用中展现了优越的性能。由于其高效性和稳定性，SDM已经成为人脸对齐领域的主要算法之一，被广泛用于人脸检测后的关键点定位，以及面部表情分析等需要精确对齐的任务中。通过有效的样本数据驱动学习，SDM能够在保持计算效率的同时，提供可靠的解决方案，极大地推动了计算机视觉领域的技术进步。
Supervised Descent Method and its Applications to Face Alignment
Xuehan Xiong Fernando De la Torre
The Robotics Institute, Carnegie Mellon University, Pittsburgh PA, 15213
xxiong@andrew.cmu.edu ftorre@cs.cmu.edu
Abstract
Many computer vision problems (e.g., camera calibra-
tion, image alignment, structure from motion) are solved
through a nonlinear optimization method. It is generally
accepted that 2
nd
order descent methods are the most ro-
bust, fast and reliable approaches for nonlinear optimiza-
tion of a general smooth function. However, in the context of
computer vision, 2
nd
order descent methods have two main
drawbacks: (1) The function might not be analytically dif-
ferentiable and numerical approximations are impractical.
(2) The Hessian might be large and not positive definite.
To address these issues, this paper proposes a Supervised
Descent Method (SDM) for minimizing a Non-linear Least
Squares (NLS) function. During training, the SDM learns
a sequence of descent directions that minimizes the mean
of NLS functions sampled at different points. In testing,
SDM minimizes the NLS objective using the learned descent
directions without computing the Jacobian nor the Hes-
sian. We illustrate the benefits of our approach in synthetic
and real examples, and show how SDM achieves state-of-
the-art performance in the problem of facial feature detec-
tion. The code is available at www.humansensing.cs.
cmu.edu/intraface.
1. Introduction
Mathematical optimization has a fundamental impact in
solving many problems in computer vision. This fact is
apparent by having a quick look into any major confer-
ence in computer vision, where a significant number of pa-
pers use optimization techniques. Many important prob-
lems in computer vision such as structure from motion, im-
age alignment, optical flow, or camera calibration can be
posed as solving a nonlinear optimization problem. There
are a large number of different approaches to solve these
continuous nonlinear optimization problems based on first
and second order methods, such as gradient descent [1] for
dimensionality reduction, Gauss-Newton for image align-
ment [22, 5, 14] or Levenberg-Marquardt for structure from
motion [8].
“I am hungry. Where is the
apple? Gotta do Gradient
descent”
𝑓 𝐱 = ℎ 𝐱 − 𝐲
2
𝑓(𝐱, 𝐲
1
)
𝐱
∗
1
𝐱
∗
3
𝐱
∗
2
(𝐛)
∆𝐱
𝟏
= 𝐑
𝑘
×
𝑓(𝐱, 𝐲
2
)
𝑓(𝐱, 𝐲
3
)
∆𝐱
𝟐
= 𝐑
𝑘
×
∆𝐱
𝟑
= 𝐑
𝑘
×
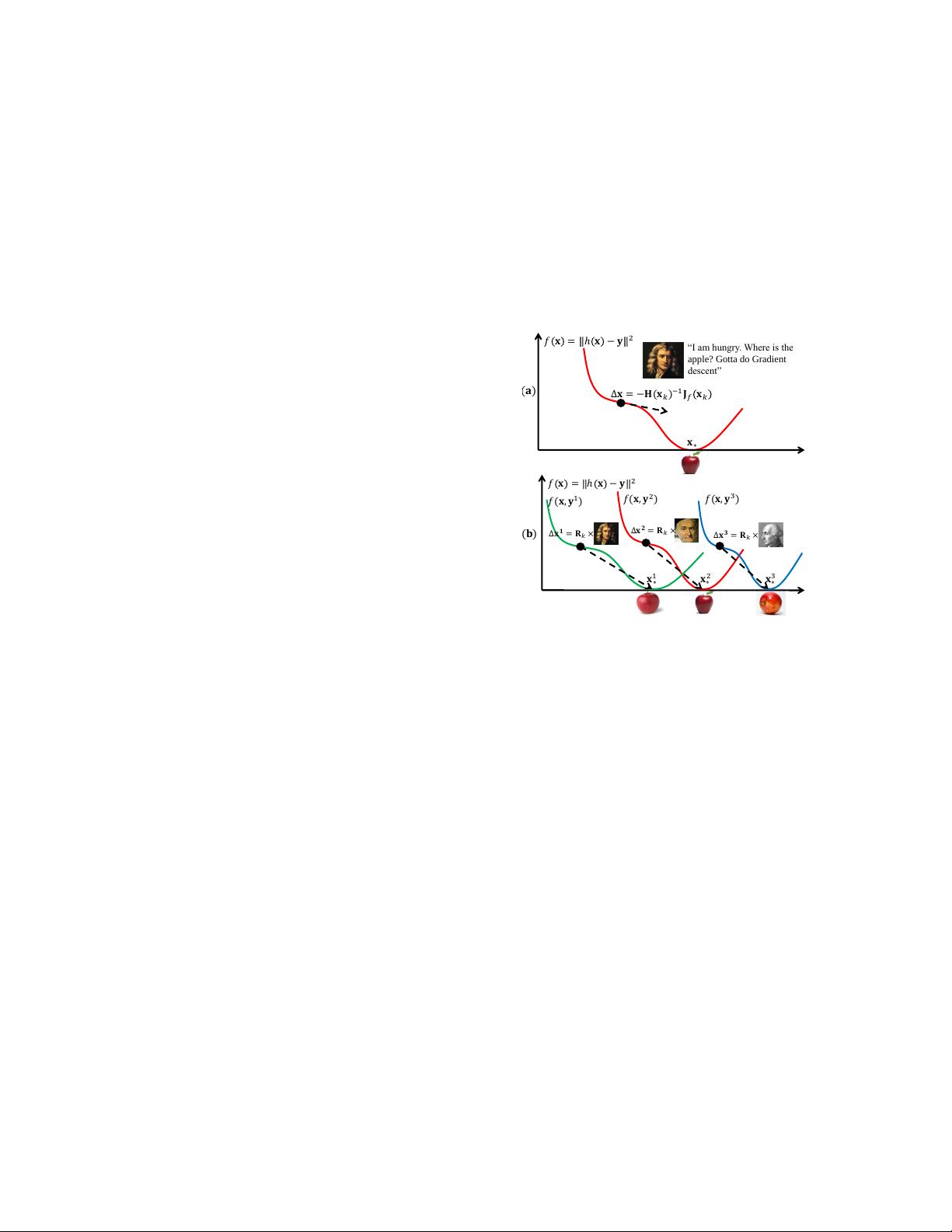
Figure 1: a) Using Newton’s method to minimize f(x). b) SDM
learns from training data a set of generic descent directions {R
k
}.
Each parameter update (∆x
i
) is the product of R
k
and an image-
specific component (y
i
), illustrated by the 3 great Mathematicians.
Observe that no Jacobian or Hessian approximation is needed at
test time. We dedicate this figure to I. Newton, C. F. Gauss, and J.
L. Lagrange for their everlasting impact on today’s sciences.
Despite its many centuries of history, the Newton’s
method (and its variants) is regarded as a major optimiza-
tion tool for smooth functions when second derivatives are
available. Newton’s method makes the assumption that
a smooth function f(x) can be well approximated by a
quadratic function in a neighborhood of the minimum. If
the Hessian is positive definite, the minimum can be found
by solving a system of linear equations. Given an initial es-
timate x
0
∈ <
p×1
, Newton’s method creates a sequence of
updates as
x
k+1
= x
k
− H
−1
(x
k
)J
f
(x
k
), (1)
where H(x
k
) ∈ <
p×p
and J
f
(x
k
) ∈ <
p×1
are the Hessian
matrix and Jacobian matrix evaluated at x
k
. Newton-type
methods have two main advantages over competitors. First,
when it converges, the convergence rate is quadratic. Sec-
ond, it is guaranteed to converge provided that the initial
estimate is sufficiently close to the minimum.
1
下载后可阅读完整内容，剩余7页未读，立即下载
2017-03-14 上传
468 浏览量
2017-11-29 上传
2023-07-24 上传
2021-09-23 上传
2021-09-25 上传
2021-05-22 上传
2021-02-11 上传
2009-12-17 上传
zlzorro
- 粉丝: 0
- 资源: 26
我的内容管理
展开
最新资源
- 构建基于Django和Stripe的SaaS应用教程
- Symfony2框架打造的RESTful问答系统icare-server
- 蓝桥杯Python试题解析与答案题库
- Go语言实现NWA到WAV文件格式转换工具
- 基于Django的医患管理系统应用
- Jenkins工作流插件开发指南：支持Workflow Python模块
- Java红酒网站项目源码解析与系统开源介绍
- Underworld Exporter资产定义文件详解
- Java版Crash Bandicoot资源库：逆向工程与源码分享
- Spring Boot Starter 自动IP计数功能实现指南
- 我的世界牛顿物理学模组深入解析
- STM32单片机工程创建详解与模板应用
- GDG堪萨斯城代码实验室：离子与火力基地示例应用
- Android Capstone项目：实现Potlatch服务器与OAuth2.0认证
- Cbit类：简化计算封装与异步任务处理
- Java8兼容的FullContact API Java客户端库介绍
