控制系统超前校正设计详解与MATLAB实现

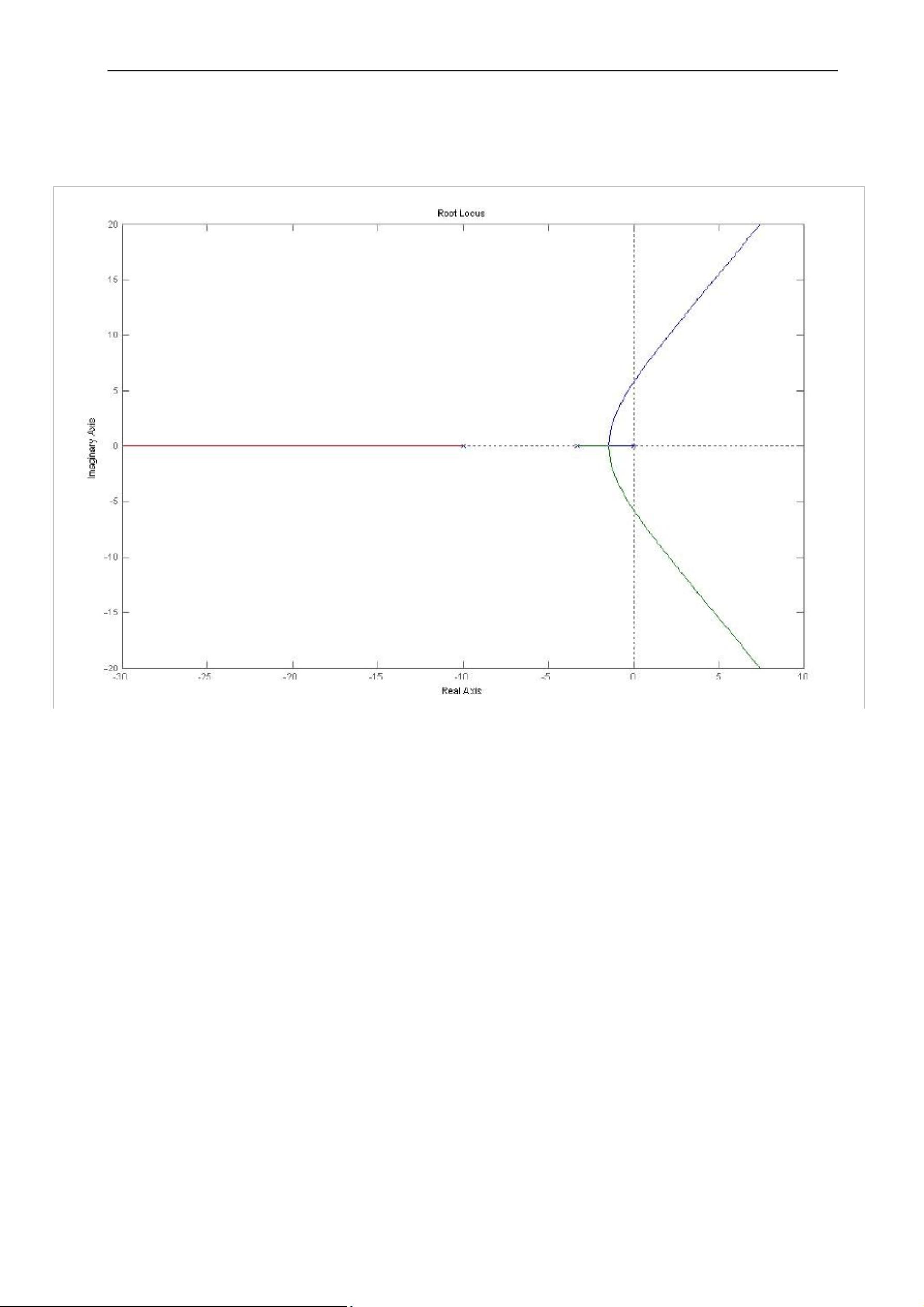
控制系统的超前校正设计是一种用于改善系统动态性能的技术，通过在系统中引入额外的相位补偿，确保系统在高频段的稳定性。以下是设计过程中的关键步骤： 1. 设计原理与步骤: - 确定开环增益：首先，根据给定的稳态性能指标（例如，静态速度误差系数 Kv），计算系统的开环增益 K。这个步骤保持系统在静态条件下的性能不变。 - 绘制未校正伯德图：利用计算得到的 K，绘制系统的开环频率响应图（伯德图），评估未校正系统的相位裕度和幅值裕度。 - 确定超前相角：量取相位裕度，计算需要补偿的超前相角 ，等于给定相位裕度指标  减去未校正系统的相位裕度 0，再加上一个附加角度 ，用来补偿因超前校正造成的负相角变化。 - 选择校正参数：根据系统剪切率选择合适的  值（如 -20dB、-40dB 或 -60dB 时对应的范围），并计算最大超前相角出现在校正后截止频率处所需的 T 参数。 - 构建超前校正传递函数：根据 T 参数，构建超前校正装置的传递函数 Gc(s)，表达为 Gc(s) = 1 + aTs / (1 + Ts)，其中 a = 1 + sin(m) / (1 - sin(m))，m 是超前相角。 - 校验与调整：校验校正后的系统性能，通过绘制校正后的伯德图，检查是否满足给定的性能指标。如果不满足，可以适当增大  值并重新调试。 2. 初始状态分析与 MATLAB 实现: - 对于初始条件，由于已知静态速度误差系数 Kv 的限制，可以通过解方程找到对应的开环增益 K。对于给定的系统动态特性（例如，G(s) = 6s(1+0.1s)(1+0.3s)），可以使用 MATLAB 的 `tf` 函数建立模型并计算其稳定性相关指标，如 margin 函数用于评估系统稳定性。 通过以上步骤，控制系统的超前校正设计旨在优化系统的动态响应，确保在高频区的稳定性和快速性，同时维持或提升系统在低频区域的稳态性能。这是一项技术性很强的工作，需对控制系统理论有深入理解，以便在实践中进行精确调整和优化。