非线性方程数值解法：增值寻根法与二分法

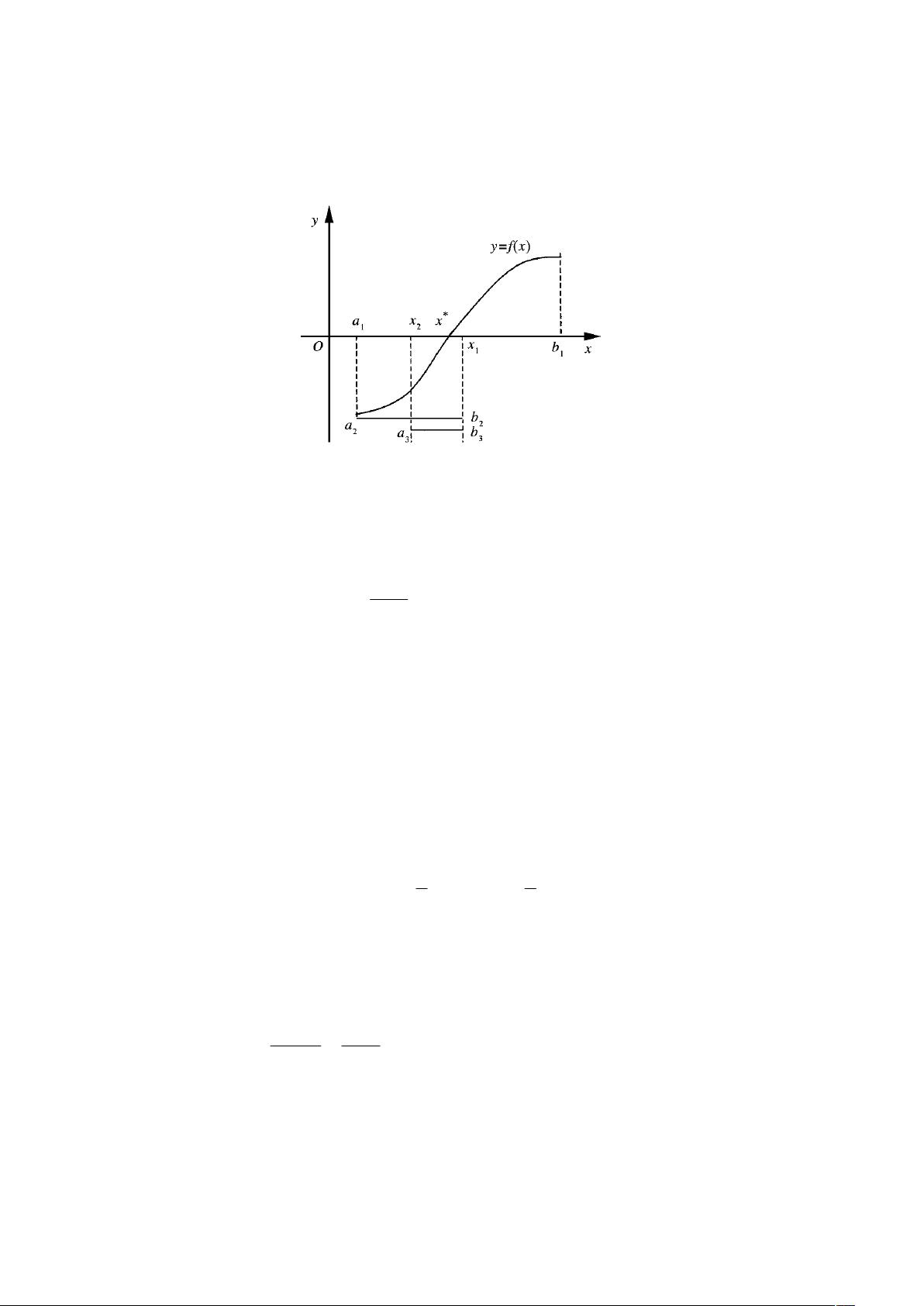
"本文介绍了非线性方程数值解法的几种常见方法，包括增值寻根法、二分法、迭代法、牛顿法以及割线法。这些方法主要应用于当解析解不存在或者计算复杂时，通过数值计算逐步逼近方程的根，直至达到预设的精度要求。" 非线性方程的数值解法在实际问题中扮演着重要角色，因为很多实际问题的数学模型往往涉及到非线性方程。对于线性方程，我们有成熟的解析解法，但非线性方程的解通常难以获得。因此，数值方法成为求解非线性方程的主要手段。 1. 增值寻根法：这种方法基于初始近似值和步长的概念。从一个初始值开始，按照一定的步长增加x的值，检查f(x)的符号变化。如果f(x)在某一点变为零，那么该点就是方程的根；如果f(x)在相邻两点符号相同，说明无根；如果符号相反，那么存在根。通过不断减小区间并调整步长，可以逐步提高根的近似精度。 2. 二分法：也称为折半法，适用于已知根位于某个闭区间内的情况。从区间两端的点开始，如果f(a)和f(b)异号，那么根必定位于(a, b)之间。将区间中点c作为新的测试点，根据f(c)的符号决定下一次分割是在[a, c]还是[c, b]。重复此过程，每次都将搜索区间减半，直到达到所需的精度。 3. 迭代法：迭代法是一类通用的方法，包括固定点迭代和拟牛顿法等。在迭代法中，通过构造一个迭代函数g(x)，使得当x趋近于根x*时，g(x)也趋近于x*。通过不断应用g(x)并更新x的值，可以逐渐逼近根。收敛速度和迭代函数的选择密切相关。 4. 牛顿法：牛顿法是一种强大的迭代法，基于泰勒展开和切线近似。假设f(x)在根x*处可导，牛顿法通过迭代公式x_{n+1} = x_n - f(x_n) / f'(x_n)寻找根。牛顿法的收敛速度快，但要求f(x)及其导数在根附近可导且导数不为零。 5. 割线法：割线法是牛顿法的一种变体，当f'(x)不易计算或不稳定时，可以用f(x_n) / (x_n - x_{n-1})作为f'(x)的近似，构建迭代公式。虽然可能比牛顿法慢，但其对函数光滑性的要求较低。 每种方法都有其适用场景和优缺点。增值寻根法和二分法简单易懂，但收敛速度较慢；牛顿法和割线法则通常更快，但需要函数的导数信息。在实际应用中，通常需要结合具体问题选择合适的方法，或者通过改进和组合这些方法来提高求解效率和精度。