SVM入门：理解支持向量机的分类与优势

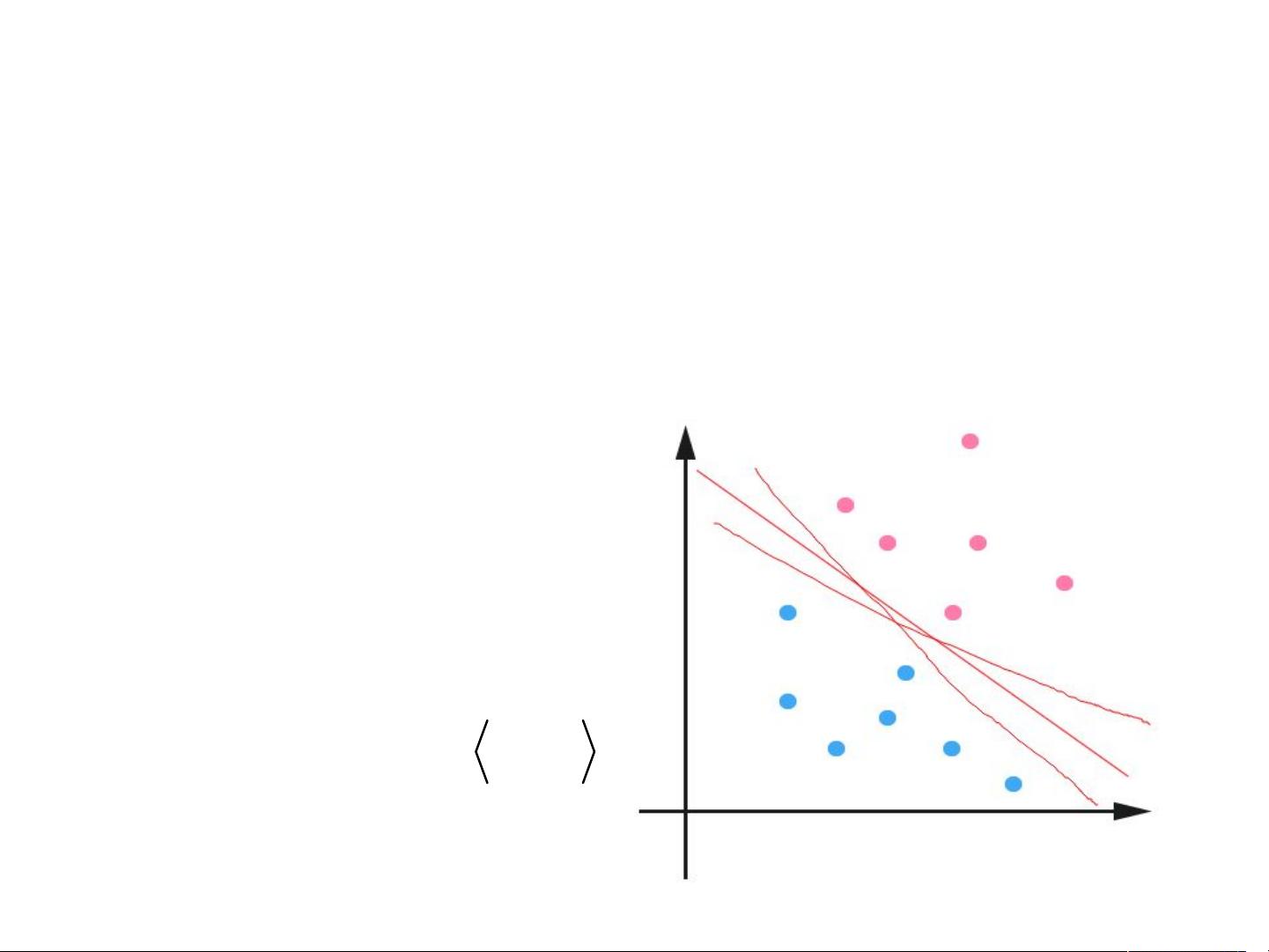
支持向量机（SVM）是一种强大的机器学习算法，最初由Cortes和Vapnik于1995年提出，它在处理小样本、非线性和高维模式识别问题时表现出色。SVM基于统计学习理论，特别是VC维理论和结构风险最小化原则，旨在通过在样本复杂性和泛化能力之间找到最佳平衡，实现对未知数据的高效分类。 SVM本质上是一个分类器，其核心思想是找到一个最优的超平面，能够将不同类别的样本分开，这个超平面被定义为支持向量（support vectors），它们是最接近超平面的边界点，决定了分类决策的稳定性。在二维或更高维度空间中，SVM利用内积（如线性函数）或称为核函数（nonlinear kernel functions）来处理非线性问题，将数据映射到更高维的空间，使得线性可分。 对于线性分类，我们可以将其视为一种简单的分类模型，比如感知机。一个典型的线性分类问题包含两类样本C1和C2，通过找到一个超平面（由斜率b和截距决定的直线，通常写作f(x) = b·x + w），使得所有样本被准确地分为正类和负类。对于新的样本，通过计算f(xi)的符号来判断其类别，如果f(xi) > 0，认为是正类；f(xi) < 0，认为是负类；f(xi) = 0则表示边界情况，可能需要进一步分析。 在表达式中，需要注意的是x表示样本的特征向量，而非简单的坐标，且f(x)代表的是决策函数，而非超平面的具体表达式。中间的分类面（零点处）是众多可能超平面中的一条，可以通过调整b和w来改变其位置。 然而，线性分类并不总是适用，特别是当数据分布是非线性的。这时，SVM引入了核函数，如径向基函数（Radial Basis Function, RBF），它允许在原始特征空间之外进行运算，实现数据的非线性映射。选择合适的核函数对于SVM性能至关重要。 在实际应用中，SVM还引入了松弛变量（slack variables）的概念，允许某些样本点稍微偏离超平面，这是为了处理现实中的噪声和不完美数据，从而提高模型的鲁棒性。通过优化带有松弛变量的目标函数，SVM能够在保证分类正确的同时，尽可能减小误差。 支持向量机作为一种重要的机器学习工具，通过巧妙地处理边界问题和非线性映射，使得它在处理复杂分类任务时展现出独特的优势。对于初学者来说，理解SVM的基本概念和原理，包括线性分类、间隔最大化、核函数以及松弛变量，是入门的重要步骤。