计算几何：线段求交算法详解

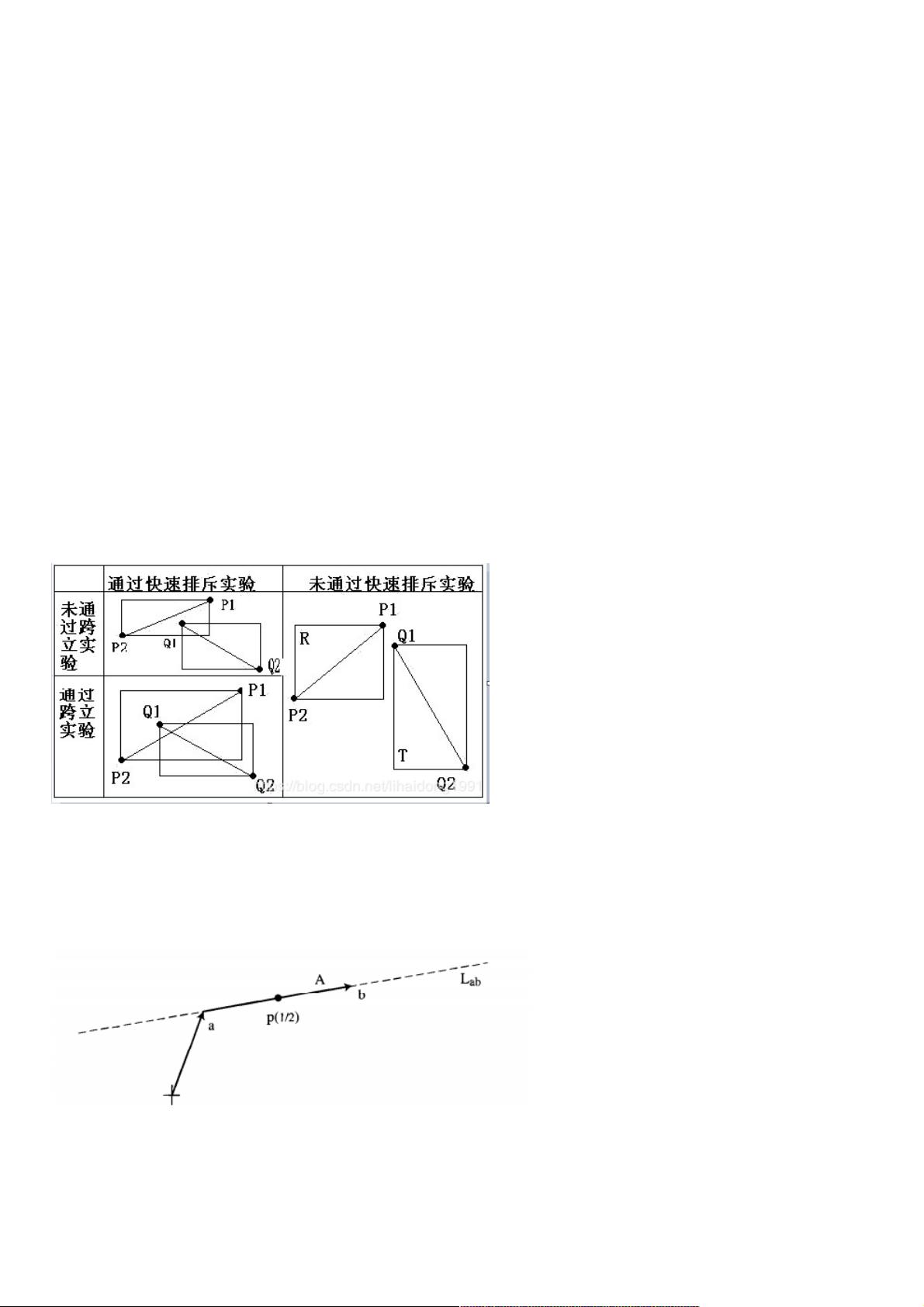
"线段求交是计算几何中的一个重要问题，涉及到二维空间中线段的位置关系判断及交点的计算。给定两条线段P1P2和Q1Q2，目标是判断它们是否相交，并在相交时找出交点。线段的位置关系包括有重合部分、无重合部分但有交点以及无交点。解决这个问题通常有两种方法：快速排斥和跨立实验结合向量法，以及直接求解线段所在直线的交点再验证交点是否在线段上。" 线段求交问题首先需要理解线段的基本概念，它是由两个点（端点）定义的有限长度的直线部分。线段P1P2和Q1Q2的坐标分别是P1(x1, y1), P2(x2, y2), Q1(x3, y3), Q2(x4, y4)。判断线段是否相交，可以通过以下步骤： **方法一：快速排斥和跨立实验** 1. **快速排斥实验**：构建以每条线段为对角线的最小外接矩形，即R(P1, P2)和T(Q1, Q2)。如果这两个矩形没有重叠，那么线段也一定不相交。 2. **跨立实验**：如果矩形R和T相交，需要进一步判断线段是否真正相交。通过比较向量(P1-Q1)和(P2-Q1)与向量(Q2-Q1)的关系，以及向量(Q1-P1)和(Q2-P1)与向量(P2-P1)的关系。如果满足以下条件，线段互相跨立且相交： - (P1-Q1)×(Q2-Q1) * (P2-Q1)×(Q2-Q1) < 0 - (Q1-P1)×(P2-P1) * (Q2-P1)×(P2-P1) < 0 其中，"×"表示向量的叉乘，用于判断两个向量是否在一条直线的两侧。 **方法二：求解直线交点并验证** 1. **求解交点**：将线段P1P2和Q1Q2视为直线Lab和Lcd，分别计算这两条直线的点斜式或一般式方程，然后联立方程组解出交点坐标。 2. **验证交点**：判断交点是否在线段上。对于交点P(x, y)，如果满足P1P2和Q1Q2的线段方程，且交点的x坐标在两个端点的x坐标之间，y坐标也在相应范围内，那么交点即为线段的交点。 这两种方法各有优缺点。快速排斥和跨立实验适用于初步快速排除不相交的情况，但在某些特殊情况下可能需要更复杂的处理，如平行线。而直接求解直线交点后再验证的方法虽然确保了结果的准确性，但需要额外的计算步骤。 在实际应用中，为了提高效率，通常会结合两种方法，先使用快速排斥实验过滤掉大部分不可能相交的线段，然后再对可能相交的线段进行精确的跨立实验或求解交点。这种方法在处理大量线段求交的问题时特别有效。