工程电磁场基础概念与定理解析

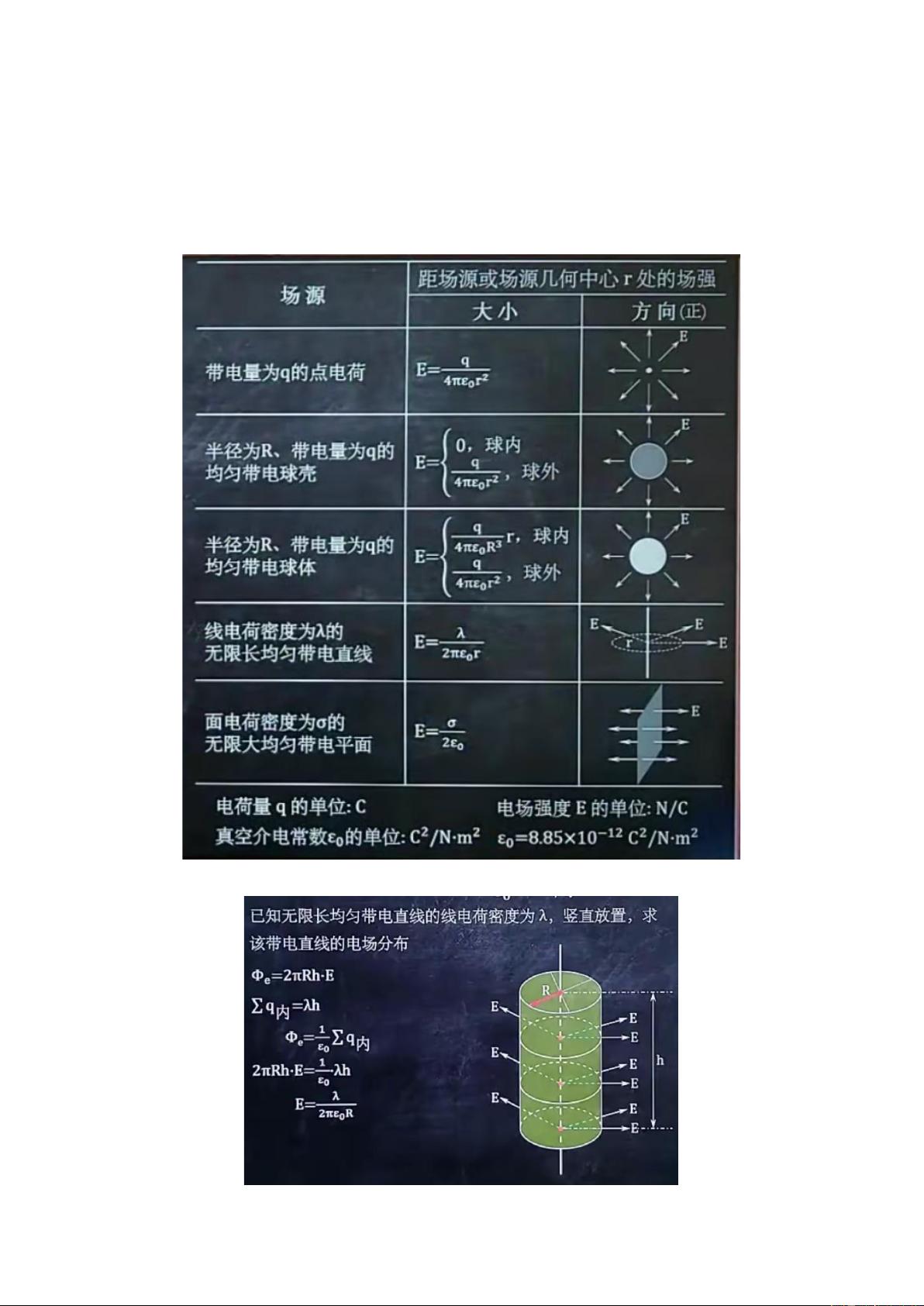
"工程电磁场(1).pdf" 本文档涵盖了工程电磁场的基础知识，主要讨论了矢量代数以及在直角坐标系下梯度、散度和旋度的计算，同时还介绍了散度定理、斯托克斯定理、亥姆霍兹定理以及电磁场的分类。 1. 矢量代数是电磁场理论的基础，包括向量的加法、减法和乘法。点乘（内积）表示两个向量在方向上的投影，而叉乘（外积）则产生一个新的向量，其方向垂直于原来的两个向量，并且根据右手定则确定。 2. 梯度、散度和旋度是描述矢量场性质的重要工具。梯度表示场强的最大增加方向，散度衡量场的源或汇的分布，旋度则表示场的旋转性。在直角坐标系中，这些运算有明确的数学表达式。 3. 散度定理（高斯定理）指出，矢量场在闭合曲面的外侧体积分等于该曲面内的源的总和，这提供了体积分和面积分之间转换的数学关系。 4. 斯托克斯定理（环路定理）表明，矢量场在闭合曲线的线积分等于该曲线围成的曲面上的旋度的面积分，揭示了线积分和面积分的等价性。 5. 亥姆霍兹定理是电磁场理论的核心，它指出，只要知道一个矢量场的散度、旋度及边界条件，就可以唯一确定这个场。它可以分解为无旋场（标量势场）和无散场（矢量势场）的组合。 6. 根据散度和旋度的特性，电磁场可以分为四类：无源无旋场（如恒定电场）、有源无旋场（如静电场）、无源有旋场（如恒定磁场）和有源有旋场（如动态电磁场，可视为静电场和恒定磁场的叠加）。 7. 两个矢量恒等式，如旋度的平方等于零（旋度的点乘等于零），是电磁场分析中的基本性质，它们在解决实际问题时具有重要的应用价值。 这些概念和定理是理解和解决电磁场问题的关键，对于工程学、物理学以及相关领域的学生和专业人士来说，掌握这些知识是至关重要的。通过深入理解并熟练运用这些原理，可以对电磁场的行为进行精确的计算和预测。