中文Comsol自定义PDE教程：理解与应用

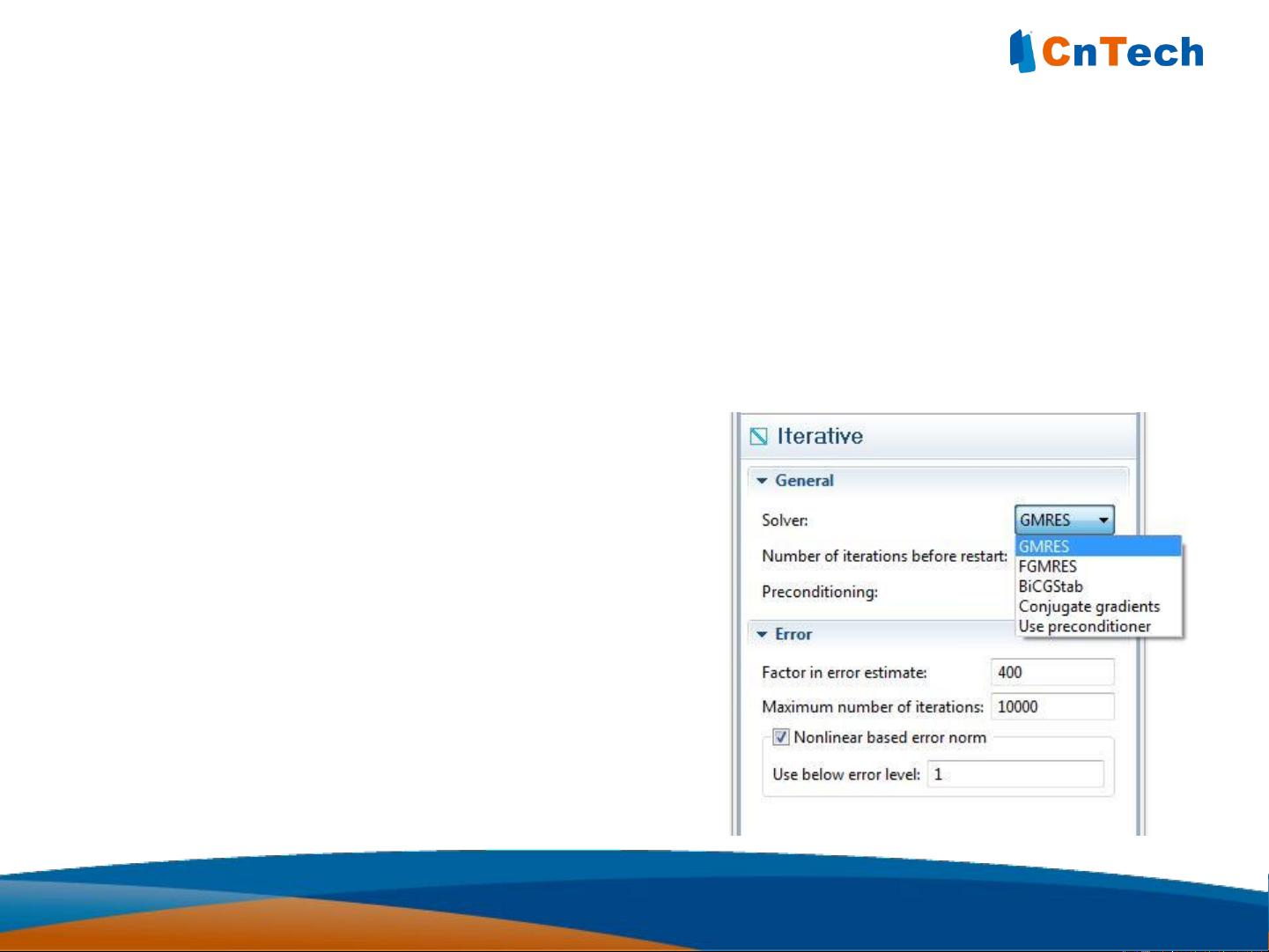
本教程是针对Comsol软件中自定义偏微分方程（PDE）的详细介绍，特别适合中文学习者入门。Comsol是一款强大的数值模拟软件，广泛应用于物理、工程和科学领域的仿真分析。教程涵盖了以下几个关键知识点： 1. **类型区分**： - 线性PDE：系数仅与空间或时间有关，不随因变量变化。 - 非线性PDE：系数依赖于因变量，增加了模型的复杂性和灵活性。 2. **自定义PDE方法**： - **系数型方程**：包括密度、阻尼系数、应力等物理参数，这些参数可以被用户根据具体问题自定义。 - **边界约束和初始条件**：在求解过程中，理解并正确设置边界条件（如固定、压力、温度等）和初始状态至关重要。 3. **方程构成**： - **质量**：系统中物质的质量分布和变化。 - **阻尼**：能量消耗，可以是质量阻尼或耗散效应。 - **扩散和对流**：物质在空间中的传播，涉及分子运动和流动。 - **源项**：输入或输出的能量，如电源或热源。 - **弹性力、初始/热应力**：物体的力学响应和初始状态。 - **惯性力**：如重力作用。 4. **守恒通量**：确保能量和物质在系统中的守恒。 - **波动方程**：描述波动现象，如声波、电磁波等，涉及到波动速度和频率。 - **输送扩散方程**：适用于描述物质的扩散和流动，如浓度或粒子的传输。 5. **方程表达式**： - 使用数学符号表示，如拉普拉斯算子（∇²）、时间导数（∂/∂t）等。 6. **方程形式与理解**： - 强解型和弱解型：两种不同的求解策略，强解型要求函数满足方程在所有点上，而弱解型允许在边界处有特定的不连续性。 - ODEs和DAEs（偏微分代数方程）：与PDE相对，前者只涉及时间变量，后者同时包含时间与空间变量。 这个教程提供了全面的指导，帮助用户了解如何在Comsol中构建和解决各种物理问题，通过实践来提升自定义PDE模型的能力，并熟练掌握边界条件和初始条件设置。无论是初学者还是进阶用户，都能从中获得有价值的知识和技巧。