公共交通系统中最短路径算法

"公共交通最短路径无向带权图是一个基于图论的计算机程序，用于模拟城市公共交通系统，找出两点间最短的交通路径。该程序使用邻接矩阵作为数据结构，存储各站点之间的联通信息，并能计算任意两点间的最短路径。程序经过调试，已确保无误，支持的最大站点数为100。" 本文将详细阐述无向带权图在公共交通系统中的应用，以及程序设计的关键方面。 一、问题分析 在公共交通系统中，每个站点被视为图中的一个节点，而站点之间的连通性则用边表示。边上的权重代表了两个站点间的距离或旅行时间。输入信息包括总站点数和存在连接的站点对，所有这些信息被用来构建邻接矩阵。 二、概要设计 1. 主界面设计 系统提供一个主菜单，用户可以通过选择不同的选项来访问如查询最短路径、查看邻接矩阵等不同功能。 2. 存储结构设计 - 图结构：使用MGraph结构体存储图的信息，包括邻接矩阵edges，顶点数n，边数e，以及一个顶点数组vexs，用于存储每个顶点的编号和其他附加信息（例如权值）。 - 邻接矩阵：二维整数数组，表示各个节点间的距离或权值。若两个节点间无直接路径，矩阵元素设为无穷大(INF)。 3. 功能实现 - 最短路径查询：Floyd算法用于计算任意两点间的最短路径，它通过动态规划更新所有节点对的最短路径。 - 打印邻接矩阵：通过两层循环遍历邻接矩阵，打印出所有节点间的权值，如果权值为无穷大，则表示无直达路径。 - 退出系统：当用户选择退出时，程序终止。 三、算法设计 1. 打印邻接矩阵的算法具有O(n^2)的时间复杂度，因为它需要遍历矩阵的每个元素。函数 DispMat() 实现了这一功能，通过判断矩阵元素是否等于INF来决定是否显示"∞"。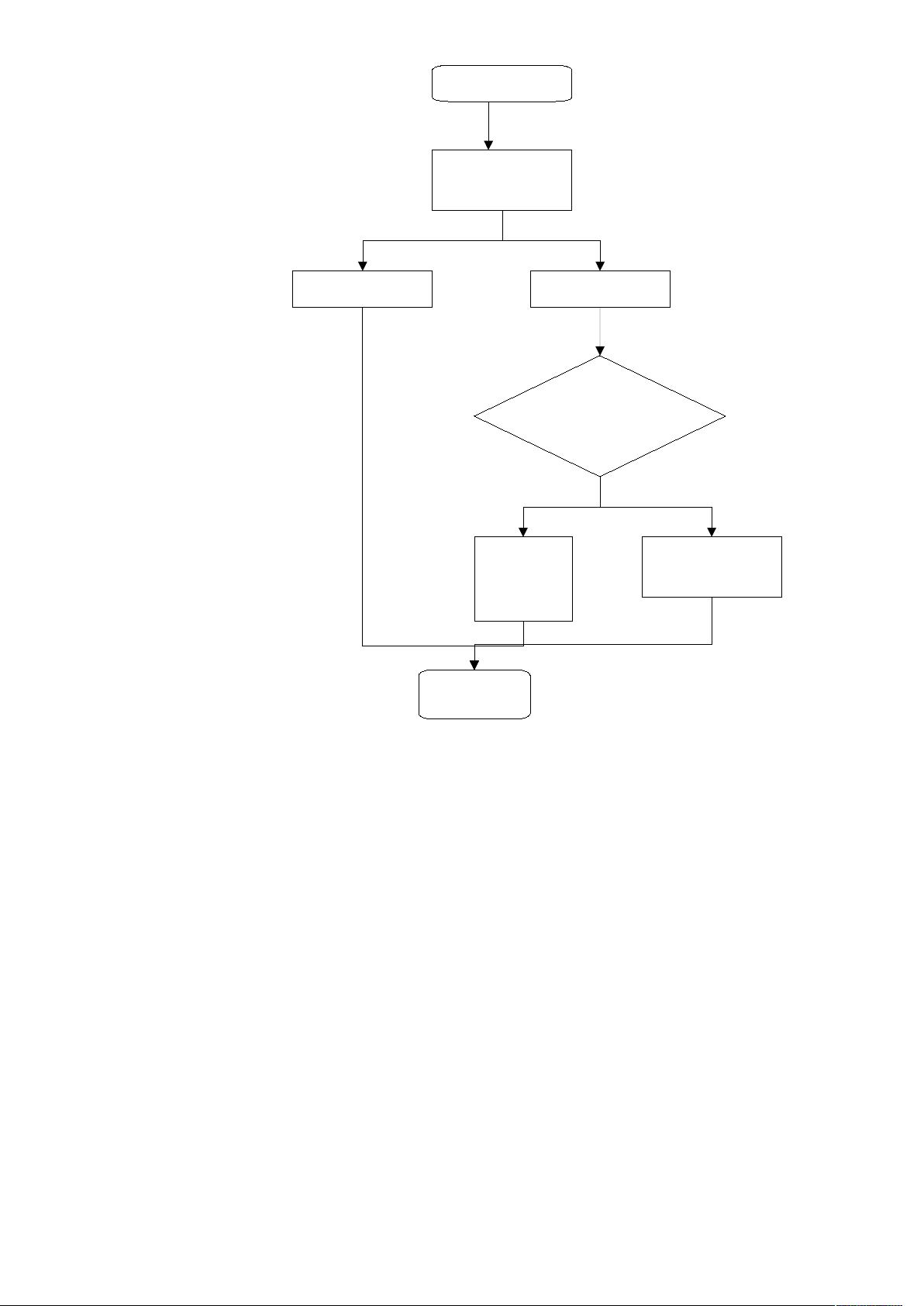 四、程序流程 程序流程通常由一个主循环控制，用户在主菜单中选择操作，根据选择调用相应函数处理，直到用户选择退出。 总结，这个公共交通最短路径无向带权图程序利用图论中的数据结构和算法，实现了城市公共交通网络的建模与最短路径查询。其核心在于邻接矩阵的构建和Floyd算法的应用，提供了友好的用户界面和高效的路径查找功能。