关系数据库系统中Top-k查询处理技术的调查

需积分: 1 188 浏览量更新于2024-07-29 收藏 1.93MB PDF 举报

"本文档是一份关于关系数据库系统中Top-k查询处理技术的调查报告，由Ihab F. Ilyas、George Besselaes和Mohamed A. Soliman撰写，来自滑铁卢大学。报告详细探讨了在处理大量数据的交互环境中，高效Top-k查询处理的重要性，特别是在Web、多媒体搜索和分布式系统中的应用。报告对当前的技术进行了描述和分类，并讨论了设计维度，包括查询模型、数据访问方法、实现层次、数据和查询的确定性以及支持的评分函数。此外，还涉及了XML领域的Top-k查询及其与关系方法的联系。" 在关系数据库系统中，Top-k查询处理技术是关键，它涉及到从海量数据中快速获取排名前k的结果。这些查询在诸如搜索引擎、推荐系统和在线分析处理等实时交互场景中扮演着重要角色。报告首先强调了高效处理Top-k查询对于性能提升的显著影响。接着，报告详细阐述了不同的设计维度： 1. **查询模型**：不同的Top-k查询模型关注于如何表达和处理查询，例如基于排序的查询、基于窗口的查询或动态更新的查询。 2. **数据访问方法**：这包括索引结构的使用，如B树、R树、倒排索引等，以及如何利用这些索引来加速Top-k查询的执行。 3. **实现层次**：处理可以在查询处理器、存储管理系统或者应用层等多个层面进行，每种层次都有其优势和挑战。 4. **数据和查询的确定性**：不确定性可能来源于数据的不精确性或查询的动态性，处理这些不确定性需要特定的策略。 5. **评分函数**：不同的应用场景需要不同的评分标准，例如基于距离、相关性或其他复杂度量的函数。报告还讨论了Top-k查询在XML数据环境中的应用，XML数据具有层次结构，处理起来更具挑战性。XML领域的Top-k查询通常需要考虑结构信息，而不仅仅是数值比较。最后，报告提到了"rank-aware processing"（排名感知处理）、"rank aggregation"（排名聚合）和"voting"等额外的关键概念，这些都是优化Top-k查询性能的重要策略。总结来说，这份报告为读者提供了一个全面的框架，理解并比较各种Top-k查询处理技术，对于数据库研究人员和系统开发者来说，是一份宝贵的参考资料。通过深入研究这些技术和方法，可以更好地设计和优化数据库系统，以满足现代大数据环境中的高性能查询需求。

11:10 I. F. Ilyas et al.

whenever p

≤ ´p

for every i. We elaborate on the impact of function monotonicity on

top-k processing in Section 6.1.

In more complex applications, a ranking function might need to be expressed as a

numeric expression to be optimized. In this setting, the monotonicity restriction of the

ranking function is relaxed to allow for more generic functions. Numerical optimization

tools as well as indexes are used to overcome the processing challenges imposed by such

ranking functions.

Another group of applications address ranking objects without specifying a ranking

function. In some environments, such as data exploration or decision making, it might

not be important to rank objects based on a speciﬁc ranking function. Instead, objects

with high quality based on different data attributes need to be reported for further

analysis. These objects could possibly be among the top-k objects of some unspeciﬁed

ranking function. The set of objects that are not dominated by any other objects, based

on some given attributes, are usually referred to as the skyline.

We classify top-k processing techniques based on the restrictions they impose on the

underlying ranking function as follows:

—Monotone ranking function. Most of the current top-k processing techniques assume

monotone ranking functions since they ﬁt in many practical scenarios, and have

appealing properties allowing for efﬁcient top-k processing. One example is Fagin

et al. [2001]. We discuss the properties of monotone ranking functions in Section 6.1.

—Generic ranking function. A few recent techniques, for example, Zhang et al. [2006],

address top-k queries in the context of constrained function optimization. The ranking

function in this case is allowed to take a generic form. We discuss the details of these

techniques in Section 6.2.

—No ranking function. Many techniques have been proposed to answer skyline-related

queries, for example, B

orzs

onyi et al. [2001] and Yuan et al. [2005]. Covering current

skyline literature in detail is beyond the scope of this survey. We believe it worth a

dedicated survey by itself. However, we brieﬂy show the connection between skyline

and top-k queries in Section 6.3.

2.6. Impact of Design Dimensions on Top-k Processing Techniques

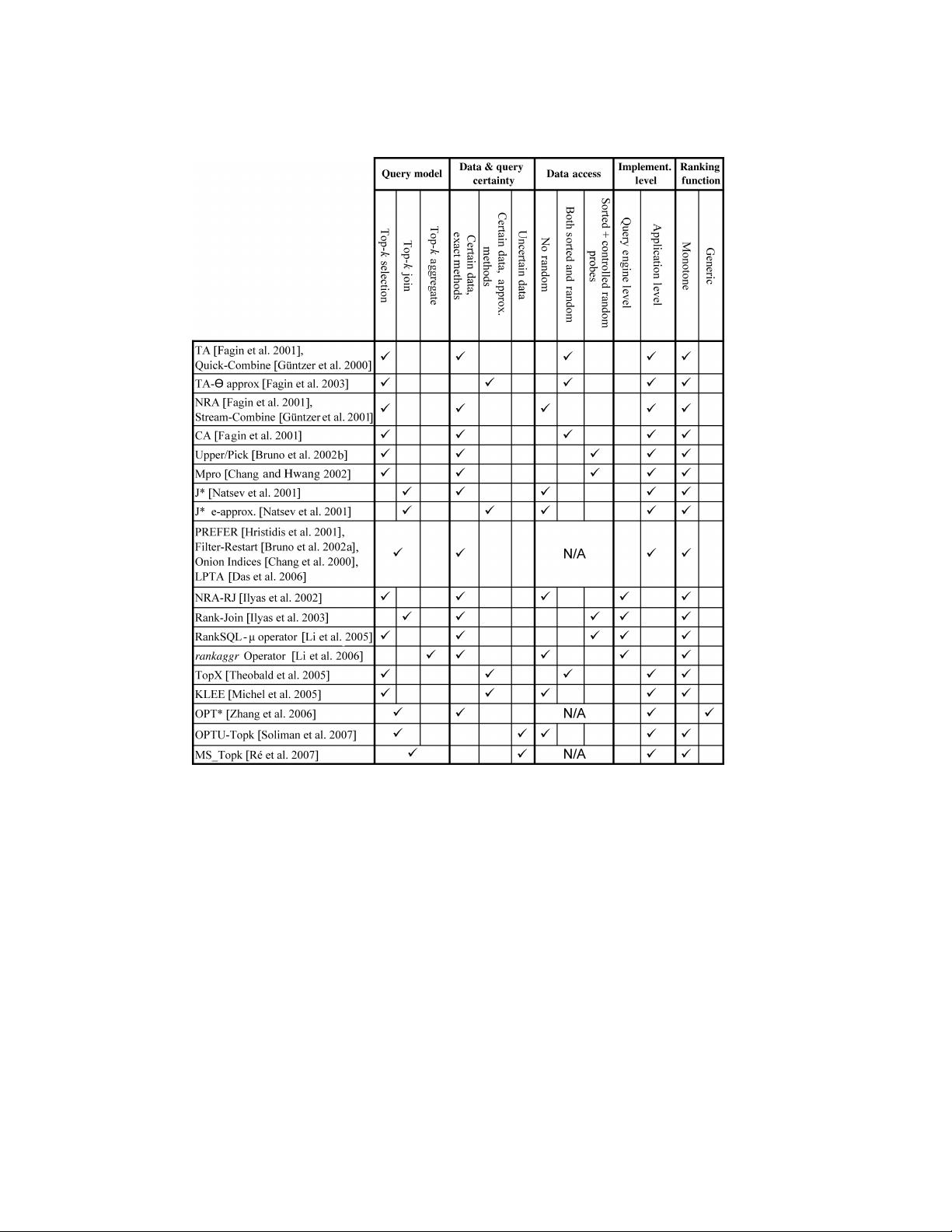
Figure 4 shows the properties of a sample of different top-k processing techniques that

we describe in this survey. The applicable categories under each taxonomy dimension

are marked for each technique. For example, TA [Fagin et al. 2001] is an exact method

that assumes top-k selection query model, and operates on certain data, exploiting

both sorted and random access methods. TA integrates with database systems at the

application level, and supports monotone ranking functions.

Our taxonomy encapsulates different perspectives to understand the processing re-

quirements of current top-k processing techniques. The taxonomy dimensions, dis-

cussed in the previous sections, can be viewed as design dimensions that impact the

capabilities and the assumptions of the underlying top-k algorithms. In the following,

we give some examples of the impact of each design dimension on the underlying top-k

processing techniques:

—Impact of query model. The query model signiﬁcantly affects the solution space of the

top-k algorithms. For example, the top-k join query model (Deﬁnition 2.2) imposes

tight integration with the query engine and physical join operators to efﬁciently

navigate the Cartesian space of join results.

—Impact of data access. Available access methods affect how different algorithms com-

pute bounds on object scores and hence affect the termination condition. For example,

ACM Computing Surveys, Vol. 40, No. 4, Article 11, Publication date: October 2008.

11:12 I. F. Ilyas et al.

—Impact of implementation level. The implementation level greatly affects the require-

ments of the top-k algorithm. For example, implementing top-k pipelined query op-

erator necessitates using algorithms that require no random access to their inputs to

ﬁt in pipelined query models; it also requires the output of the top-k algorithm to be

a valid input to another instance of the algorithm [Ilyas et al. 2004a]. On the other

hand, implementation on the application level does not have these requirements.

More details are given in Section 4.2.1.

—Impact of ranking function. Assuming monotone ranking functions allows top-k pro-

cessing techniques to beneﬁt from the monotonicity property to guarantee early-out

of query answers. Dealing with nonmonotone functions requires more sophisticated

bounding for the scores of unexplored answers. Existing indexes in the database

are currently used to provide such bounding, as addressed in Xin et al. [2007]

(Section 6).

3. DATA ACCESS

In this section, we discuss top-k processing techniques that make different assumptions

about available access methods supported by data sources. The primary data access

methods are sorted access, random access, and a combination of both methods. In sorted

access, objects are accessed sequentially ordered by some scoring predicate, while for

random access, objects are directly accessed by their identiﬁers.

The techniques presented in this section assume multiple lists (possibly located at

separate sources) that rank the same set of objects based on different scoring predicates.

A score aggregation function is used to aggregate partial objects’ scores, obtained from

the different lists, to ﬁnd the top-k answers.

The cost of executing a top-k query, in such environments, is largely inﬂuenced by

the supported data access methods. For example, random access is generally more

expensive than sorted access. A common assumption in all of the techniques discussed

in this section is the existence of at least one source that supports sorted access. We

categorize top-k processing techniques, according to the assumed source capabilities,

into the three categories described in the next sections.

3.1. Both Sorted and Random Access

Top-k processing techniques in this category assume data sources that support both

access methods, sorted and random. Random access allows for obtaining the overall

score of some object right after it appears in one of the data sources. The Thresh-

old Algorithm (TA) and Combined Algorithm (CA) [Fagin et al. 2001] belong to this

category.

Algorithm 1 describes the details of TA. The algorithm scans multiple lists, repre-

senting different rankings of the same set of objects. An upper bound T is maintained

for the overall score of unseen objects. The upper bound is computed by applying the

scoring function to the partial scores of the last seen objects in different lists. Notice that

the last seen objects in different lists could be different. The upper bound is updated

every time a new object appears in one of the lists. The overall score of some seen object

is computed by applying the scoring function to object’s partial scores, obtained from

different lists. To obtain such partial scores, each newly seen object in one of the lists is

looked up in all other lists, and its scores are aggregated using the scoring function to

obtain the overall score. All objects with total scores that are greater than or equal to T

can be reported. The algorithm terminates after returning the kth output. Example 3.1

illustrates the processing of TA.

ACM Computing Surveys, Vol. 40, No. 4, Article 11, Publication date: October 2008.

剩余57页未读，继续阅读

billmaths

粉丝: 0
资源: 2

关系数据库系统中Top-k查询处理技术的调查

【中国房地产业协会-2024研报】2024年第三季度房地产开发企业信用状况报告.pdf

【中国银行-2024研报】美国大选结果对我国芯片产业发展的影响和应对建议.pdf

RM1135开卡工具B17A

毕业设计&课设_宿舍管理系统：计算机毕业设计项目.zip

毕业设计&课设_画手交易管理系统：Java 毕设项目.zip

跑腿平台系统 微信小程序+SSM毕业设计 源码+数据库+论文+启动教程.zip

Visual Studio 2013 Shell

【UBS-2024研报】US Equity Strategy _Earnings Brief 3Q24 November.pdf

Mentor Graphics ModelSim SE 2020.4 x64安装包

毕业设计&课设_智慧社区管理系统：Java 毕设项目.zip

最新资源

跑腿平台系统微信小程序+SSM毕业设计源码+数据库+论文+启动教程.zip