图优化SLAM基础教程：英文高清解读
需积分: 13 63 浏览量
更新于2024-08-05
收藏 2.43MB PDF 举报
"该资源是一个关于图优化SLAM的高清英文教程，可能包含详细的教学材料、讨论、统计数据和作者简介。教程出自IEEE Intelligent Transportation Systems Magazine的一篇2010年12月发表的文章，由四位作者合作完成，包括Giorgio Grisetti, Rainer Kümmerle, Cyrill Stachniss和Wolfram Burgard。这些作者还参与了其他相关项目，如Flourish项目，涉及空中数据收集与分析以及精准农业的自动化地面干预。该教程的doi为10.1109/MITS.2010.939925，可在DBLP上找到。"
图优化SLAM（Simultaneous Localization and Mapping，同时定位与建图）是机器人学和计算机视觉领域中的一个关键问题，它允许机器人在未知环境中自主导航并构建环境的地图。这篇教程详细介绍了基于图的SLAM方法，这种方法将SLAM问题转化为一个优化问题，通过构建一个包含传感器测量、先验知识和机器人运动模型的因子图来解决。
在图优化SLAM中，每个节点通常代表一个状态，例如机器人的位置或地图中的特征点，而边表示不同状态之间的关系或测量。通过最小化图中所有边的累积误差，可以找到最优状态估计，实现机器人定位和地图构建的精确同步。
文章可能涵盖了以下几个核心知识点：
1. **基础概念**：介绍SLAM的基本问题，包括机器人定位、环境建图的挑战和目标，以及为什么图优化方法适合处理这些问题。
2. **因子图**：详细解释因子图的结构，包括节点和边的定义，以及如何用它们来表示传感器测量和先验信息。
3. **优化算法**：可能包括Gauss-Newton法、Levenberg-Marquardt算法等非线性优化方法，用于求解因子图的全局最优解。
4. **SLAM框架**：介绍如何构建图优化SLAM的完整框架，包括数据关联、异常值处理、平滑和约束添加等步骤。
5. **实验与应用**：展示实际应用场景，可能包括室内导航、自动驾驶等，以及通过实验结果验证图优化SLAM的有效性和性能。
6. **相关工作**：回顾和比较其他SLAM方法，如EKF-SLAM（扩展卡尔曼滤波SLAM）、粒子滤波SLAM等，突出图优化SLAM的优势。
7. **未来方向**：探讨图优化SLAM的潜在改进点，如实时性、鲁棒性、在线学习等方面的研究。
这篇教程对于深入理解图优化SLAM的理论和实践具有很高的价值，适合机器人学、计算机视觉和自动化领域的研究人员和学生阅读学习。通过学习，读者能够掌握如何利用图优化技术解决SLAM问题，并将其应用于实际的机器人系统中。
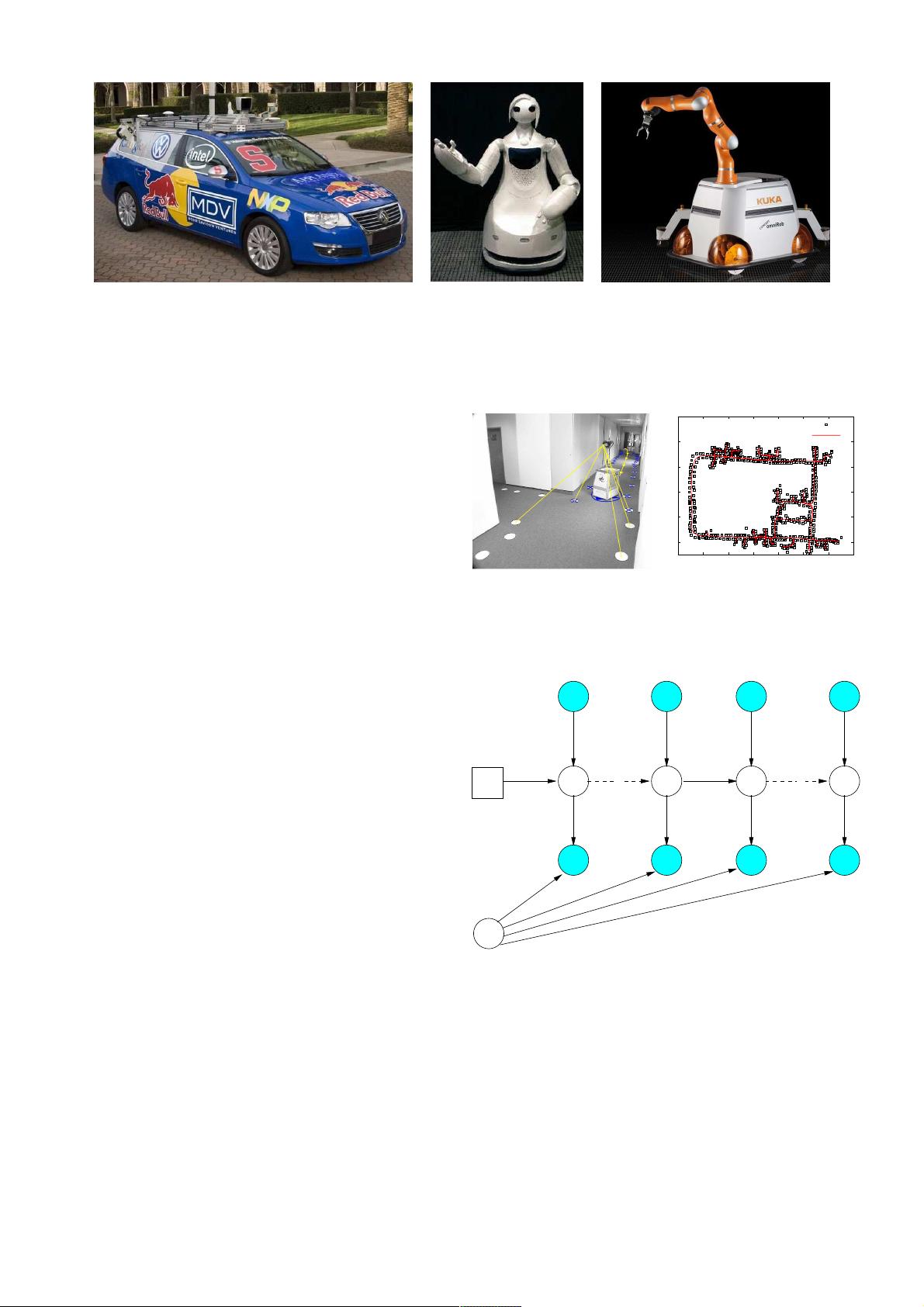
2
(a) (b) (c)
Fig. 1. Applications of SLAM technology. (a) An autonomous instrumented car developed at Stanford. This car can acquire maps by utilizing only its
on-board sensors. These maps can be subsequently used for autonomous navigation. (b) The museum guide robot TPR-Robina developed by Toyota (picture
courtesy of Toyota Motor Company). This robot acquires a new map every time the museum is reconfigured. (c) The KUKA Concept robot “Omnirob”, a
mobile manipulator designed autonomously navigate and operate in the environment with the sole use of its on-board sensors (picture courtesy of KUKA
Roboter GmbH).
variables x
1:T
= {x
1
, . . . , x
T
}. While moving, it acquires a
sequence of odometry measurements u
1:T
= {u
1
, . . . , u
T
}
and perceptions of the environment z
1:T
= {z
1
, . . . , z
T
}.
Solving the full SLAM problem consists of estimating the
posterior probability of the robot’s trajectory x
1:T
and the
map m of the environment given all the measurements plus
an initial position x
0
:
p(x
1:T
, m | z
1:T
, u
1:T
, x
0
). (1)
The initial position x
0
defines the position of the map and
can be chosen arbitrarily. For convenience of notation, in the
remainder of this document we will omit x
0
. The poses x
1:T
and the odometry u
1:T
are usually represented as 2D or 3D
transformations in SE(2) or in SE(3), while the map can be
represented in different ways. Maps can be parametrized as
a set of spatially located landmarks, by dense representations
like occupancy grids, surface maps, or by raw sensor measure-
ments. The choice of a particular map representation depends
on the sensors used, on the characteristics of the environment,
and on the estimation algorithm. Landmark maps [28], [22] are
often preferred in environments where locally distinguishable
features can be identified and especially when cameras are
used. In contrast, dense representations [33], [12], [9] are
usually used in conjunction with range sensors. Independently
of the type of the representation, the map is defined by the
measurements and the locations where these measurements
have been acquired [17], [18]. Figure 2 illustrates three typical
dense map representations for 3D and 2D: multilevel surface
maps, point clouds and occupancy grids. Figure 3 shows a
typical 2D landmark based map.
Estimating the posterior given in (1) involves operating in
high dimensional state spaces. This would not be tractable if
the SLAM problem would not have a well defined structure.
This structure arises from certain and commonly done assump-
tions, namely the static world assumption and the Markov
assumption. A convenient way to describe this structure is via
the dynamic Bayesian network (DBN) depicted in Figure 4.
A Bayesian network is a graphical model that describes a
stochastic process as a directed graph. The graph has one node
for each random variable in the process, and a directed edge (or
-20
-10
0
10
20
30
-50 -40 -30 -20 -10 0 10 20
landmarks
trajectory
Fig. 3. Landmark based maps acquired at the German Aerospace Center. In
this setup the landmarks consist in white circles painted on the ground that
are detected by the robot through vision, as shown in the left image. The right
image illustrates the trajectory of the robot and the estimated positions of the
landmarks. These images are courtesy of Udo Frese and Christoph Hertzberg.
x
0
x
1
x
t−1
x
t
x
T
u
1
u
t−1
u
t
u
T
z
1
z
t−1
z
t
z
T
m
Fig. 4. Dynamic Bayesian Network of the SLAM process.
arrow) between two nodes models a conditional dependence
between them.
In Figure 4, one can distinguish blue/gray nodes indicating
the observed variables (here z
1:T
and u
1:T
) and white nodes
which are the hidden variables. The hidden variables x
1:T
and m model the robot’s trajectory and the map of the
environment. The connectivity of the DBN follows a recurrent
剩余11页未读，继续阅读
140 浏览量
164 浏览量
211 浏览量
1441 浏览量
105 浏览量
2019-03-20 上传
668 浏览量
2018-08-16 上传
点击了解资源详情
orrinzhang
- 粉丝: 0
- 资源: 5
我的内容管理
展开
最新资源
- Alaamimi
- StoryScrip-crx插件
- btw_deploy_test：btw的playtest存储库
- 29500-g30.zip
- Single Click for for Google:trade_mark: Apps-crx插件
- getallpropertynames:获取原型链中的所有属性名称
- github-bot：GitHub自动处理问题，PR，发布机器人
- JavaScript和DOM操作
- VB隐藏或显示“开始”菜单中的各种选项
- mriscv:带有C＆Rust应用程序的Mini RISC-V 32位计算机
- SQLserver2008.rar
- Geekmarks client-crx插件
- ExeBinder.7z
- competencies
- 建筑电气自动化控制技术的相关分析 (1).rar
- MyFoody:第2周作业-食品应用
