二叉查找树与数据结构——树的探索与操作

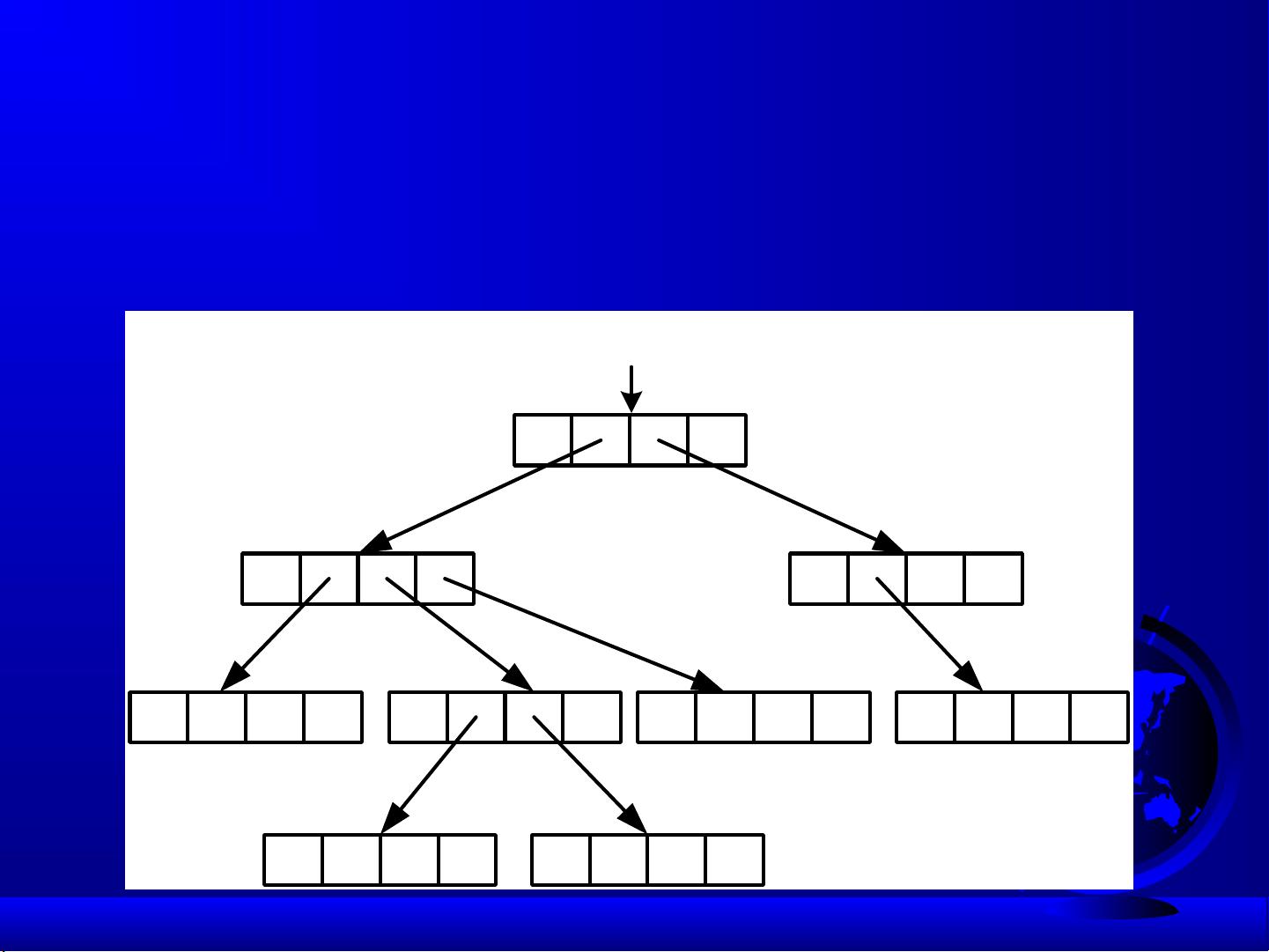
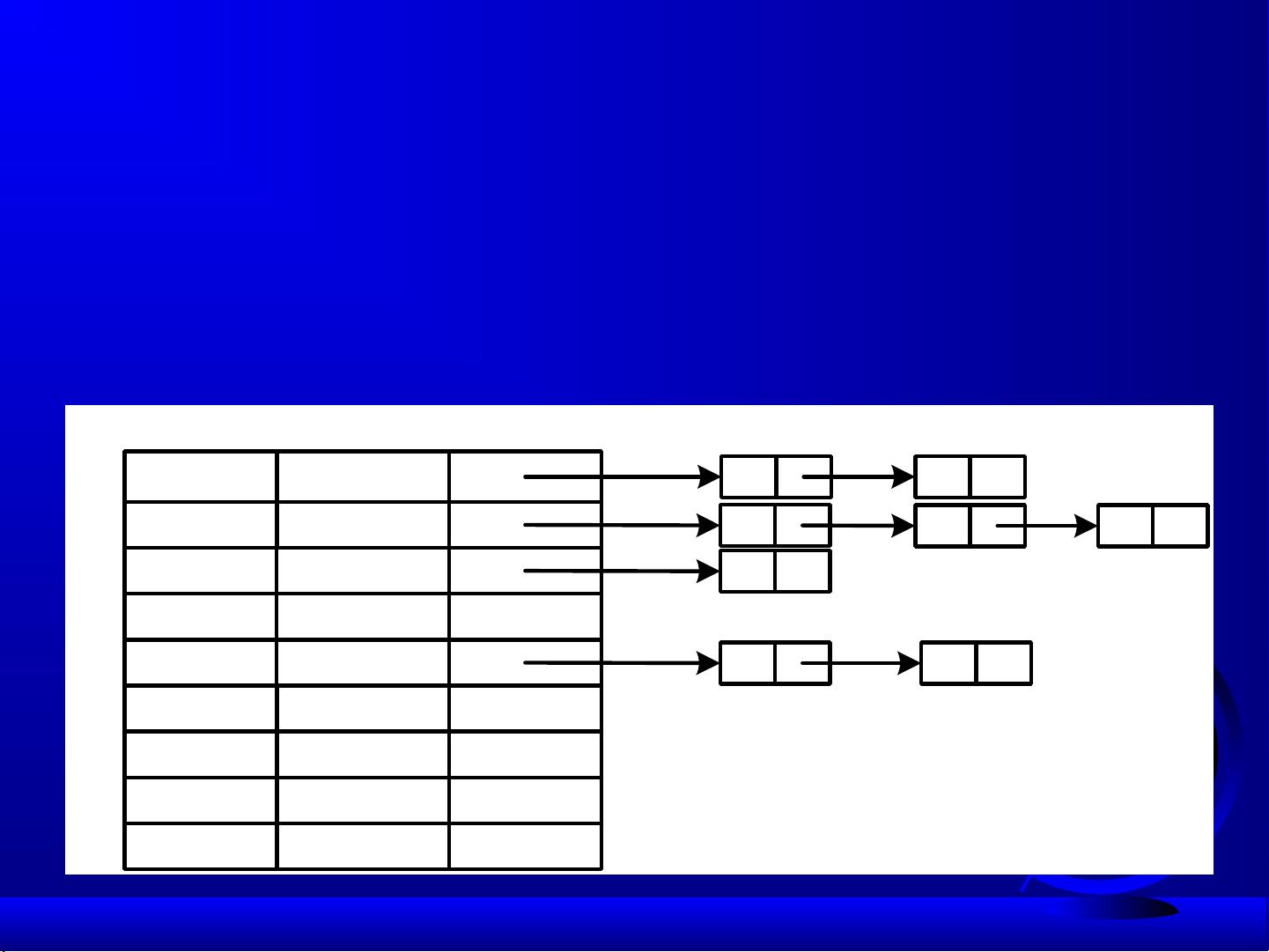
"这是一份关于二叉树算法和数据结构的PPT，重点讲解了二叉树，特别是二叉查找树的概念、表示方法以及操作，包括查找、插入和删除等基本操作，还提到了哈夫曼编码的实现。" 在计算机科学中，树是一种非常重要的非线性数据结构，它模仿自然界中的层次关系。二叉树是树的一个特例，每个节点最多有两个子节点，分别被称为左子节点和右子节点。二叉树的概念对于理解和实现许多高效的算法至关重要，如搜索、排序和数据压缩。 二叉查找树（Binary Search Tree，BST）是一种特殊的二叉树，它遵循以下规则： 1. 每个节点的左子树只包含比其小的节点。 2. 每个节点的右子树只包含比其大的节点。 3. 左右子树都必须是二叉查找树。 学习二叉树的目标通常包括理解以下几个方面： 1. **树的定义**：树是由n个节点构成的层次结构，其中n可以是0，表示空树。根节点是树的起点，没有前驱节点，而其余节点分为多个子树，每个子树自身也是一个树结构。 2. **节点性质**：节点由数据元素和指向子节点的指针组成。节点的度是指其子树的数量，叶子节点是度为0的节点，分支节点是度不为0的节点。孩子节点是节点的子树根，双亲节点是孩子的上级节点，兄弟节点是共享同一双亲的节点。 3. **树的度与深度**：树的度是所有节点度的最大值，节点的层次是从根到节点的路径上分支的数量，树的深度是所有节点层次的最大值。 4. **无序树与有序树**：无序树的子节点没有特定顺序，而在有序树中，子节点的顺序是有意义的。 5. **森林**：森林是由多棵树组成的集合。 在二叉查找树中执行操作： - **查找**：从根节点开始，按照二叉查找树的规则比较节点值，直到找到目标节点或确定不存在。 - **插入**：在适当位置插入新节点，保持二叉查找树的性质。 - **删除**：删除节点需要考虑多种情况，如删除叶子节点、单子节点和有多个子节点的节点。 此外，二叉树还有多种遍历方式，如前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根），这些遍历方法在处理树数据时非常有用。 最后，二叉树在实际应用中的一种经典应用是哈夫曼编码，这是一种用于数据压缩的高效方法。通过构建最优的二叉树（哈夫曼树），可以为每个字符分配一个唯一的二进制编码，使得频繁出现的字符编码较短，从而提高压缩效率。 理解和掌握二叉树及其操作对于学习和实践算法至关重要，因为它们在计算机科学的许多领域，如数据库、编译器设计和图形学中都有广泛应用。这份PPT详细介绍了这些概念，是学习二叉树的好资源。