掌握高级数据结构：平衡二叉树、可并优先队列与线段树详解

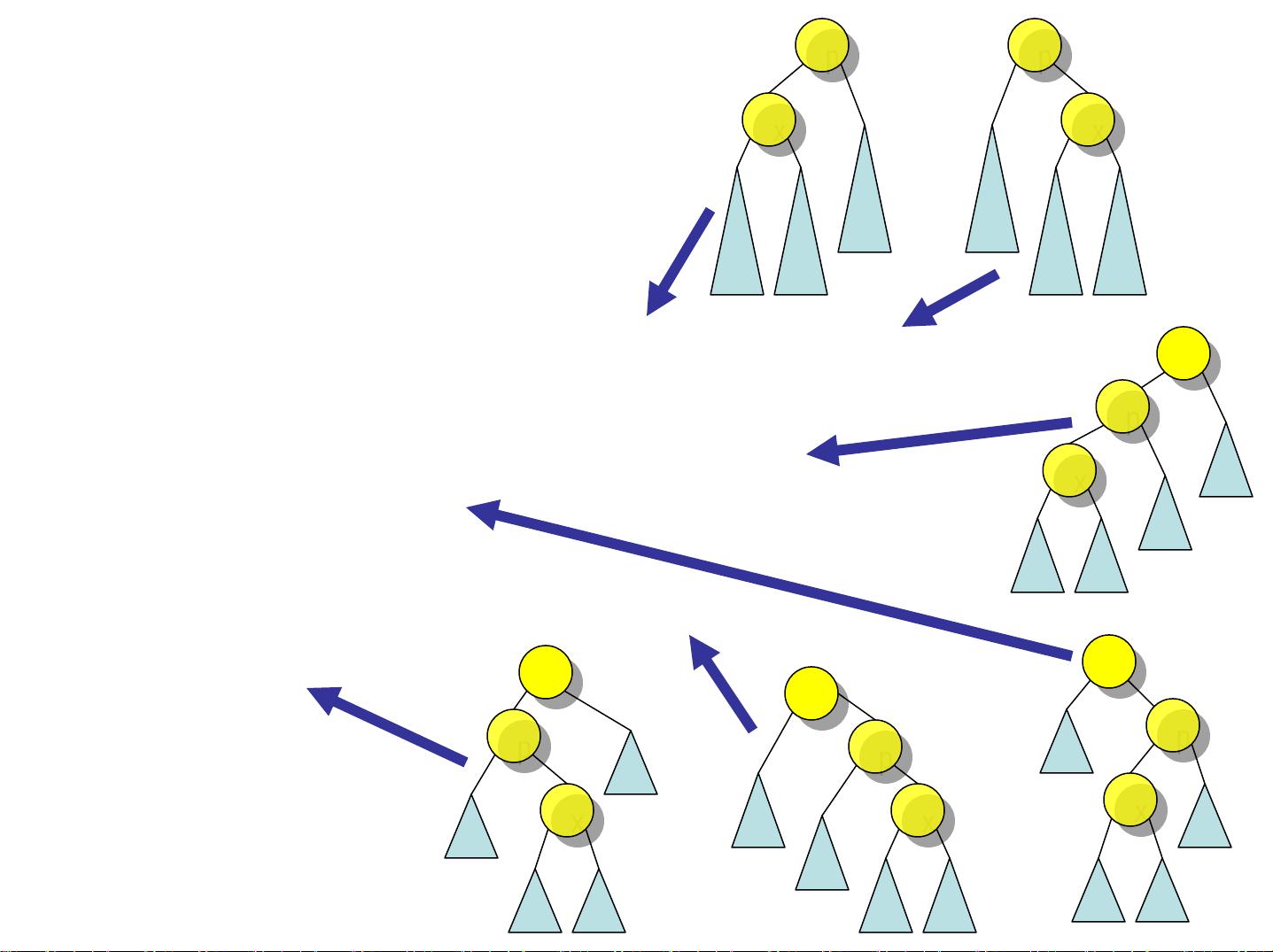
高级数据结构课程由刘汝佳主讲，涵盖了一系列关键的数据结构技术，包括平衡二叉树、可并优先队列、线段树和树状数组的基础以及RMQ与LCA。课程的核心内容首先从平衡二叉树开始，它是一种特殊的二叉搜索树，其中每个节点的左子树小于根节点，右子树大于根节点。基本的平衡二叉树如二叉查找树(BST)在查找、插入和删除操作中的时间复杂度为O(h)，其中h表示树的高度。为了提高效率，平衡二叉树如AVL树引入了高度限制，即每个节点的左右子树高度差不超过1，这确保了树的高度大致上是O(logn)，从而在各种操作中保持快速响应。 AVL树的维护通过旋转操作实现，单旋转用于解决某个子树高度过大导致不平衡的情况，例如当左孩子高度大于右孩子高度+1时，通过将右孩子作为旋转轴进行调整。双旋转则涉及更复杂的场景，当祖父节点和孙子节点共线或不共线时，通过先向左旋转再向右旋转来重新平衡树结构。在插入新元素时，会沿着路径找到第一个不平衡的祖父节点，然后进行相应的旋转。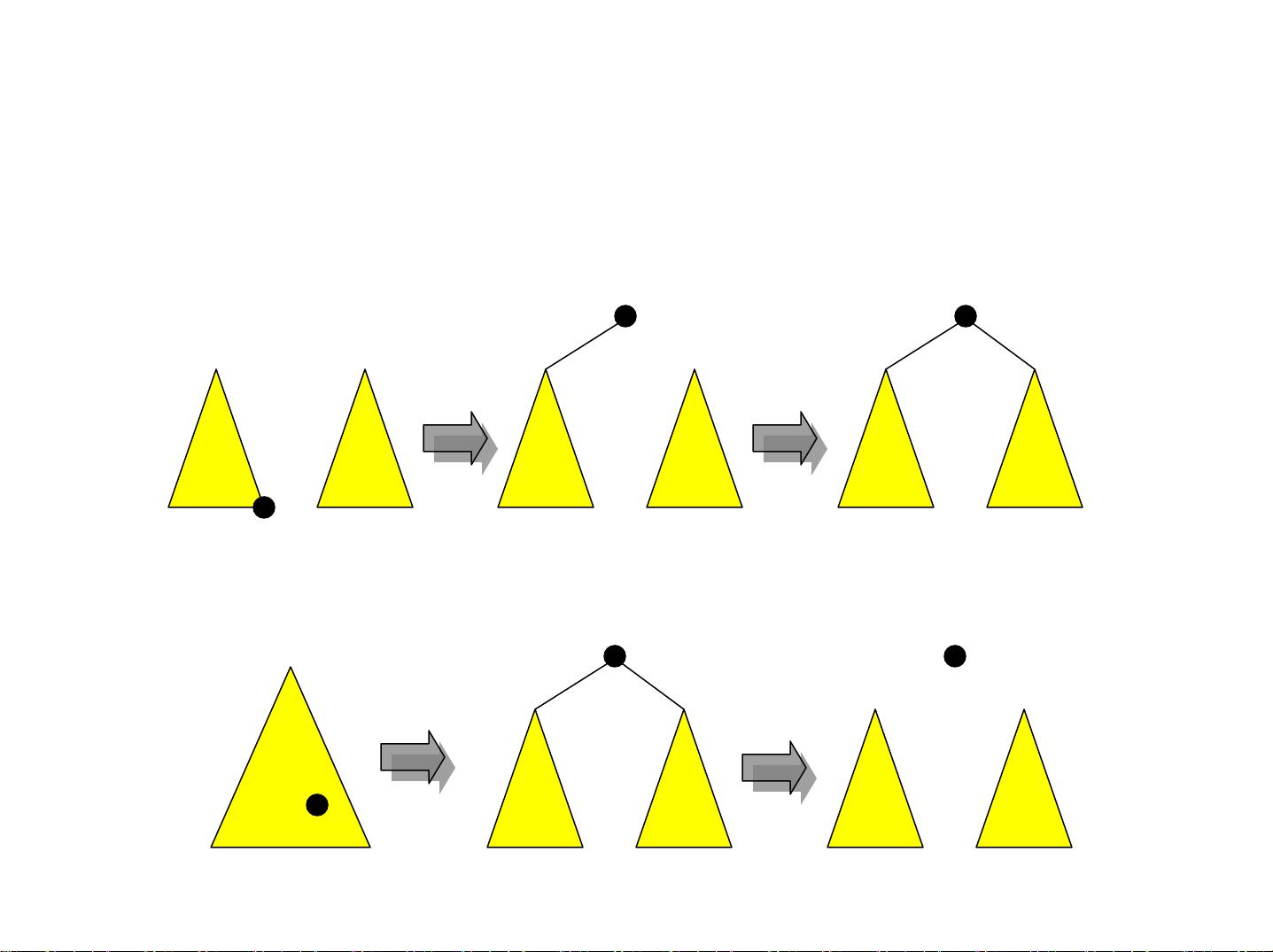 接下来，课程介绍的是可并优先队列，这是一种特殊的队列，能够合并两个已排序的队列，同时保持高效查询最小元素的能力。线段树和树状数组是另一种高效的数据结构，它们分别用于处理区间查询和更新问题，常用于求解范围最大值、最小值等问题，其查询时间复杂度通常为O(logn)。 最后，课程涵盖了Range Minimum Query (RMQ)和Least Common Ancestor (LCA)的概念。RMQ用于在一个数组中查找一个区间的最小值，而LCA则是查找两个节点最近的公共祖先。这些高级数据结构在图论、动态规划等算法中起着关键作用，能够大大提高复杂问题的解决效率。 刘汝佳的高级数据结构课程深入浅出地讲解了这些数据结构的原理、实现和应用场景，对于提高算法设计和优化能力具有重要意义。学习者将不仅掌握基本的数据结构理论，还能学会如何在实际编程中灵活运用这些工具。