U
V
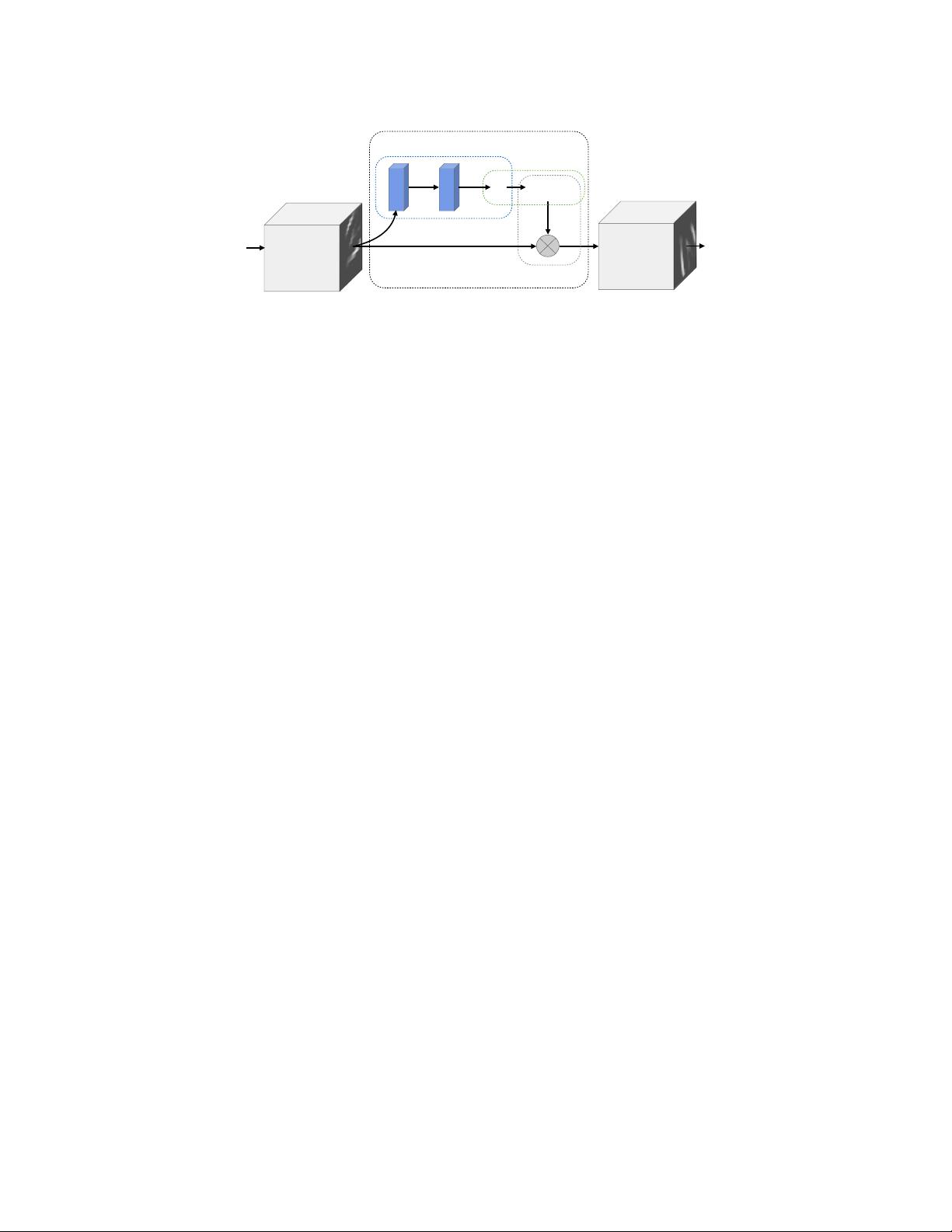
Localisation net
Sampler
Spatial Transformer
Grid !
generator
Figure 2: The architecture of a spatial transformer module. The input feature map U is passed to a localisation
network which regresses the transformation parameters θ. The regular spatial grid G over V is transformed to
the sampling grid T
θ
(G), which is applied to U as described in Sect. 3.3, producing the warped output feature
map V . The combination of the localisation network and sampling mechanism defines a spatial transformer.
need for a differentiable attention mechanism, while [14] use a differentiable attention mechansim
by utilising Gaussian kernels in a generative model. The work by Girshick et al. [11] uses a region
proposal algorithm as a form of attention, and [7] show that it is possible to regress salient regions
with a CNN. The framework we present in this paper can be seen as a generalisation of differentiable
attention to any spatial transformation.
3 Spatial Transformers
In this section we describe the formulation of a spatial transformer. This is a differentiable module
which applies a spatial transformation to a feature map during a single forward pass, where the
transformation is conditioned on the particular input, producing a single output feature map. For
multi-channel inputs, the same warping is applied to each channel. For simplicity, in this section we
consider single transforms and single outputs per transformer, however we can generalise to multiple
transformations, as shown in experiments.
The spatial transformer mechanism is split into three parts, shown in Fig. 2. In order of computation,
first a localisation network (Sect. 3.1) takes the input feature map, and through a number of hidden
layers outputs the parameters of the spatial transformation that should be applied to the feature map
– this gives a transformation conditional on the input. Then, the predicted transformation parameters
are used to create a sampling grid, which is a set of points where the input map should be sampled to
produce the transformed output. This is done by the grid generator, described in Sect. 3.2. Finally,
the feature map and the sampling grid are taken as inputs to the sampler, producing the output map
sampled from the input at the grid points (Sect. 3.3).
The combination of these three components forms a spatial transformer and will now be described
in more detail in the following sections.
3.1 Localisation Network
The localisation network takes the input feature map U ∈ R
H×W ×C
with width W , height H and
C channels and outputs θ, the parameters of the transformation T
θ
to be applied to the feature map:
θ = f
loc
(U). The size of θ can vary depending on the transformation type that is parameterised,
e.g. for an affine transformation θ is 6-dimensional as in (10).
The localisation network function f
loc
() can take any form, such as a fully-connected network or
a convolutional network, but should include a final regression layer to produce the transformation
parameters θ.
3.2 Parameterised Sampling Grid
To perform a warping of the input feature map, each output pixel is computed by applying a sampling
kernel centered at a particular location in the input feature map (this is described fully in the next
section). By pixel we refer to an element of a generic feature map, not necessarily an image. In
general, the output pixels are defined to lie on a regular grid G = {G
i
} of pixels G
i
= (x
t
i
, y
t
i
),
forming an output feature map V ∈ R
H
0
×W
0
×C
, where H
0
and W
0
are the height and width of the
grid, and C is the number of channels, which is the same in the input and output.
3









