RPCA：低秩与稀疏分解原理与应用

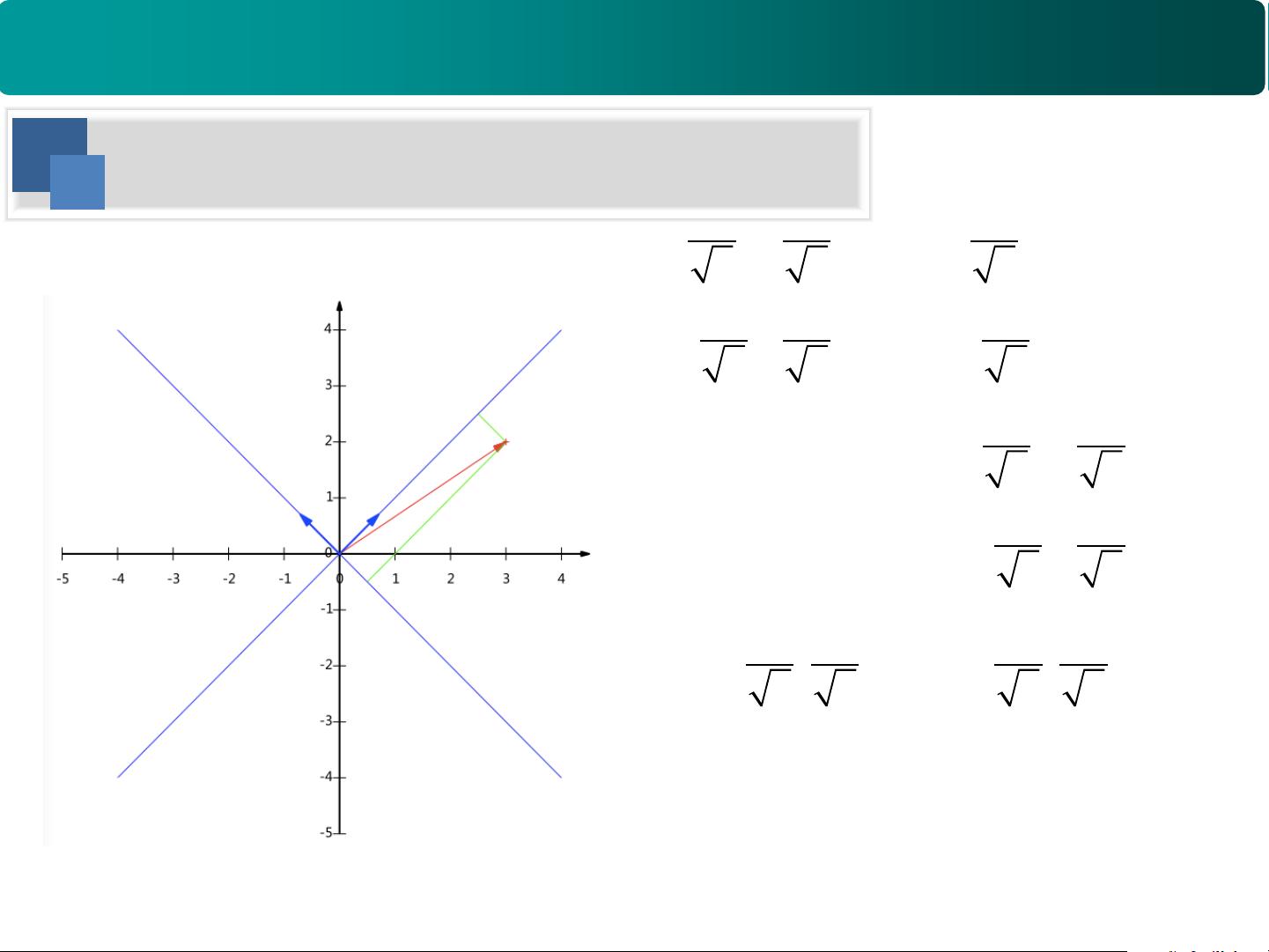
RPCA，全称为Robust Principal Component Analysis（鲁棒主成分分析），是一种在数据挖掘和机器学习领域中广泛应用的技术，特别是在处理含有低秩结构和稀疏噪声的数据时。问题背景是给定一组观测数据，其中包含一个低秩成分和一个稀疏成分（通常认为是潜在的异常或错误）。低秩成分代表数据中的主要模式或趋势，而稀疏成分则表示不常见的、孤立的噪声点。 直观理解PCA（Principal Component Analysis），它是一种线性降维方法，用于找到数据中最重要的特征方向。在二维示例中，如果我们将数据看作是由两个维度（x和y）构成的，PCA试图找到这两个维度之间的关系，并将数据投影到一个新的坐标系统中，其中第一个轴（主成分）捕捉大部分数据的方差。PCA通过计算协方差矩阵来确定这个方向，协方差矩阵反映了变量间线性关系的强度。 在PCA的直观图中，我们看到一个一维子空间和原始数据分布。原始数据（X）由一个信号（δsignal）和噪声（δnoise）组成。PCA通过分解数据为一个低秩矩阵A（主要由样本的均值和共线性构成）和一个稀疏矩阵B（对应于离群值或异常值），来实现去噪和简化数据。当向量B（表示为单位向量）与A进行内积时，其结果相当于A在B的方向上的投影长度。 在矩阵形式中，PCA的原理表现为将原始数据矩阵通过A和B的线性组合进行重构。矩阵乘法在这里起到了关键作用，它不仅实现了数据的降维，还通过选择合适的基向量（A和B）分离了低秩和稀疏部分。在具体应用中，如矩阵减法，可以观察到矩阵A和B的组合如何减去噪声（B）以恢复接近原始低秩结构的矩阵（A' = A - B）。 PCA的优化问题通常涉及最小化重构误差的同时保持低秩性和稀疏性，这可以通过非负矩阵分解（NMF）或其他优化算法来解决。对于鲁棒PCA（RPCA），算法设计上加入了对异常值鲁棒性的考虑，使得在存在大量噪声或异常值的情况下也能准确地分离出低秩和稀疏成分。 总结来说，RPCA是一个强大的工具，它在处理含有低秩和稀疏特性的数据时具有显著优势。通过深入理解PCA的核心原理，我们可以更好地利用RPCA技术进行数据分析和预处理，提高模型的稳定性和准确性。