MATLAB模拟：傅里叶级数与频谱分析

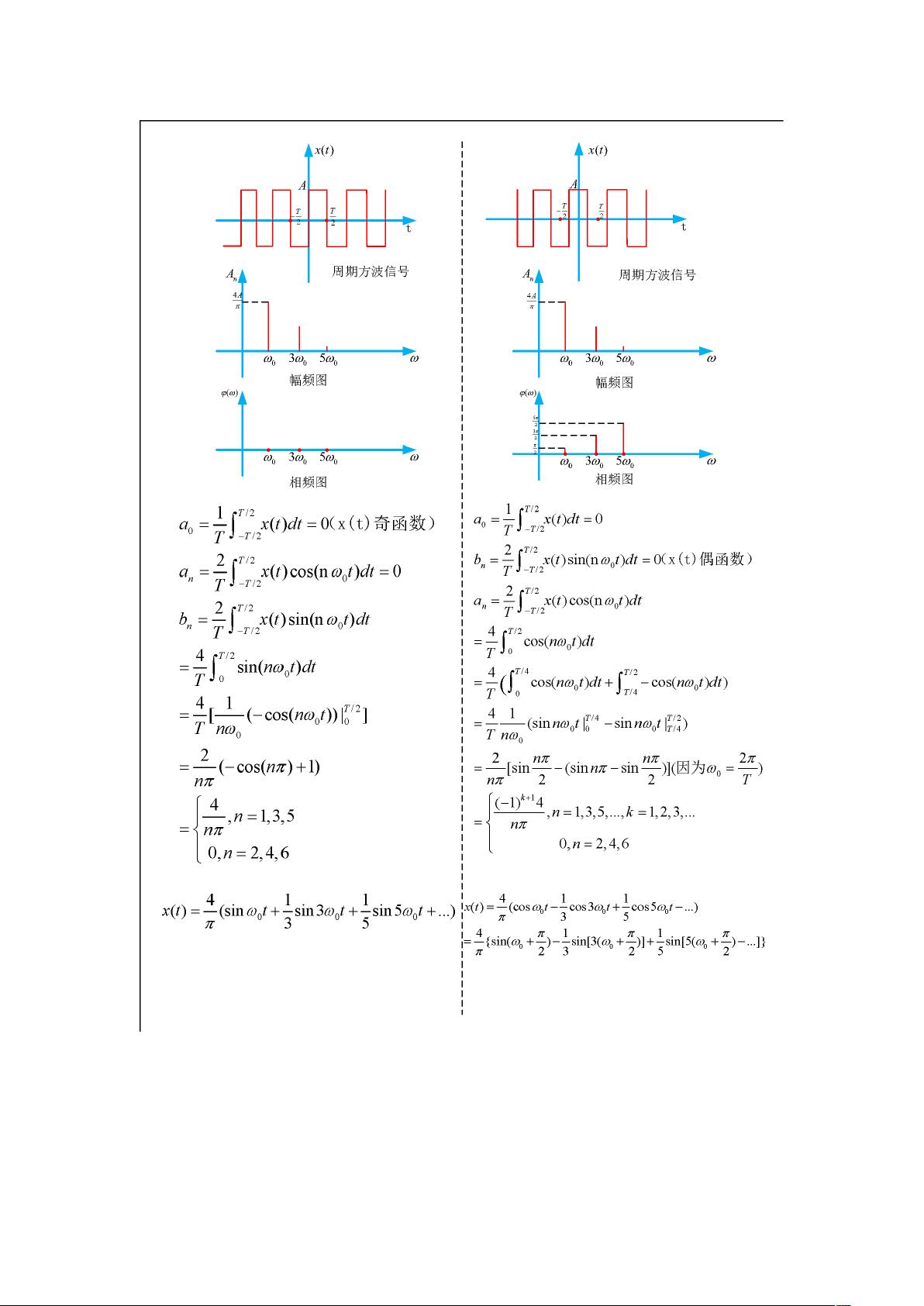
"这篇文档主要介绍了如何借助MATLAB来理解和应用傅里叶级数和傅里叶变换，通过实例深入解析了这两个概念，并探讨了它们在信号处理中的应用。" 傅里叶级数和傅里叶变换是信号分析和处理领域的核心工具，用于将时域中的复杂信号分解为简单的正弦和余弦波形。MATLAB作为一个强大的数学计算软件，提供了直观的方式去理解和模拟这些变换。 1. 傅里叶级数 是将周期性信号分解为无限个正弦和余弦函数的叠加。对于周期性信号f(t)，如果它满足狄利赫里条件（如在每个周期内连续或有限个第一类间断点，有限个极值点，且绝对可积），那么可以表示为傅里叶级数。使用欧拉公式，傅里叶级数可以转换为复指数形式，其中振幅cn被转换为振幅和相位结合的Fn。 2. 频谱分析 是傅里叶变换的应用，它揭示了信号在频域中的特性。一个周期信号的频谱由振幅谱和相位谱组成，分别对应于频率与振幅的关系和频率与相位的关系。在MATLAB中，可以通过`fft`函数计算傅里叶变换，并使用`plot`函数绘制幅度频谱和相位频谱，以理解信号的频率成分。 在文档给出的例子中，展示了一个周期信号f(t)的幅度频谱的计算过程。MATLAB程序首先定义了信号f(t)的表达式，然后使用`fftshift`和`fft`函数计算其傅里叶变换，并对结果进行归一化。通过`subplot`函数，程序同时绘制了时域波形和频域的幅度谱，帮助我们直观地看到信号的频域特性。 3. 快速傅里叶变换(FFT) 是傅里叶变换的一种高效算法，特别适用于大量数据的处理。在上述例子中，`fft`函数用于计算傅里叶变换，而`fftfreq`函数（虽然没有在提供的代码中使用，但通常用于创建频率轴）可以生成对应于输入信号频率的频率向量。`N`表示采样点数，`T`为采样间隔，`D`则用于将时间域转换为频域。 4. 信号处理函数 MATLAB提供了一系列信号处理相关的函数，如滤波、频谱分析等，这些在理解傅里叶变换及其应用时非常有用。例如，`filter`函数用于滤波操作，`spectrogram`函数用于显示信号的瞬时频谱，而`pwelch`函数则用于功率谱估计。 通过MATLAB的这些功能，我们可以对信号进行深入的分析，比如识别信号中的噪声、提取特征频率、检测调制或解调信号，甚至重建原始信号。这在通信、音频处理、图像分析等诸多领域都有着广泛的应用。因此，熟练掌握MATLAB中的傅里叶级数和傅里叶变换对于理解和解决实际问题至关重要。